Giải mục 3 trang 67, 68 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 3 trang 67, 68 SGK Toán 11 tập 1 - Chân trời sáng tạo
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Toán 11 tập 1 Chân trời sáng tạo. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, vì vậy chúng tôi luôn cố gắng mang đến những giải pháp tốt nhất để giúp bạn học tập hiệu quả.
Bài viết này sẽ tập trung vào việc giải mục 3 trang 67, 68, giúp bạn hiểu rõ các khái niệm và phương pháp giải bài tập liên quan.
Từ một hình vuông có cạnh bằng 1, tô màu một nửa hình vuông, rồi tô màu một nửa hình còn lại và cứ tiếp tục như vậy (xem Hình 2).
Hoạt động 4
Từ một hình vuông có cạnh bằng 1, tô màu một nửa hình vuông, rồi tô màu một nửa hình còn lại và cứ tiếp tục như vậy (xem Hình 2).
a) Xác định diện tích \({u_k}\) của phần hình được tô màu lần thứ \(k\left( {k = 1,2,3,...} \right)\).
b) Tính tổng diện tính \({S_n}\) của phần hình được tô màu sau lần tô thứ \(n\left( {n = 1,2,3,...} \right)\).
c) Tìm giới hạn \(\lim {S_n}\) và so sánh giới hạn này với diện tích hình vuông ban đầu.
Phương pháp giải:
a) Dựa vào đề bài, ta đưa ra công thức tổng quát của \({u_k}\) dựa vào công thức số hạng tổng quát của cấp số nhân có số hạng đầu \({u_1}\) và công bội \(q\): \({u_k} = {u_1}.{q^{k - 1}}\).
b) Áp dụng công thức tính tổng \({S_n}\) của \(n\) số hạng đầu của cấp số nhân có số hạng đầu \({u_1}\) và công bội \(q\): \({S_n} = {u_1}.\frac{{1 - {q^n}}}{{1 - q}}\).
c) Áp dụng các phép toán về giới hạn hữu hạn của dãy số và công thức tính giới hạn cơ bản: \(\lim {q^n} = 0\), với \(q\) là số thực thỏa mãn \(\left| q \right| < 1\).
Lời giải chi tiết:
a) Theo đề bài, ta thấy \(\left( {{u_k}} \right)\) là cấp số nhân với số hạng đầu \({u_1} = \frac{1}{2}\), công bội \(q = \frac{1}{2}\).
Vậy \({u_k} = {u_1}.{q^{k - 1}} = \frac{1}{2}.{\left( {\frac{1}{2}} \right)^{k - 1}} = {\left( {\frac{1}{2}} \right)^k} = \frac{1}{{{2^k}}}\).
b) \(\left( {{u_n}} \right)\) là cấp số nhân với số hạng đầu \({u_1} = \frac{1}{2}\), công bội \(q = \frac{1}{2}\).
Vậy \({S_n} = {u_1}.\frac{{1 - {q^n}}}{{1 - q}} = \frac{1}{2}.\frac{{1 - {{\left( {\frac{1}{2}} \right)}^n}}}{{1 - \frac{1}{2}}} = \frac{1}{2}.\frac{{1 - {{\left( {\frac{1}{2}} \right)}^n}}}{{\frac{1}{2}}} = 1 - {\left( {\frac{1}{2}} \right)^n}\).
c) \(\lim {S_n} = \lim \left( {1 - {{\left( {\frac{1}{2}} \right)}^n}} \right) = \lim 1 - \lim {\left( {\frac{1}{2}} \right)^n}\).
\(\lim 1 = 1\) vì 1 là hằng số.
\(\left| {\frac{1}{2}} \right| = \frac{1}{2} < 1\) nên \(\lim {\left( {\frac{1}{2}} \right)^n} = 0\)
Vậy \(\lim {S_n} = \lim 1 - \lim {\left( {\frac{1}{2}} \right)^n} = 1 - 0 = 1\)
Giới hạn này bằng diện tích của hình vuông ban đầu.
Thực hành 4
Tính tổng của cấp số nhân lùi vô hạn: \(1 + \frac{1}{3} + {\left( {\frac{1}{3}} \right)^2} + ... + {\left( {\frac{1}{3}} \right)^n} + ...\).
Phương pháp giải:
Áp dụng công thức tính tổng của cấp số nhân lùi vô hạn có số hạng đầu \({u_1}\) và công bội \(q\): \(S = {u_1} + {u_2} + ... + {u_n} + ... = \frac{{{u_1}}}{{1 - q}}\)
Lời giải chi tiết:
Tổng trên là tổng của cấp số nhân lùi vô hạn có số hạng đầu \({u_1} = 1\) và công bội \(q = \frac{1}{3}\) nên
\(1 + \frac{1}{3} + {\left( {\frac{1}{3}} \right)^2} + ... + {\left( {\frac{1}{3}} \right)^n} + ... = \frac{1}{{1 - \frac{1}{3}}} = \frac{3}{2}\).
Vận dụng 1
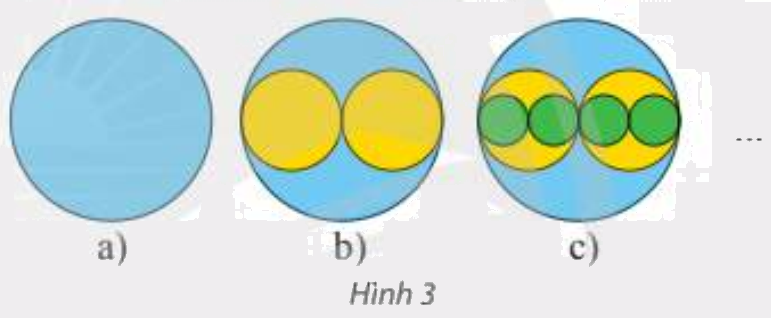
Từ tờ giấy, cắt một hình tròn bán kính \(R\left( {cm} \right)\) như Hình 3a. Tiếp theo, cắt hai hình tròn bán kính \(\frac{R}{2}\) rồi chồng lên hình tròn đầu tiên như Hình 3b. Tiếp theo, cắt bốn hình tròn bán kính \(\frac{R}{4}\) rồi chồng lên các hình trước như Hình 3c. Cứ thế tiếp tục mãi. Tính tổng diện tích của các hình tròn.

Phương pháp giải:
Đưa tổng diện tích của các hình tròn về tổng của cấp số nhân lùi vô hạn rồi áp dụng công thức tính tổng của cấp số nhân lùi vô hạn có số hạng đầu \({u_1}\) và công bội \(q\): \(S = {u_1} + {u_2} + ... + {u_n} + ... = \frac{{{u_1}}}{{1 - q}}\)
Lời giải chi tiết:
Giả sử các hình tròn bán kính \({R_1} = R,{R_2} = \frac{R}{2},{R_3} = \frac{R}{4} = \frac{R}{{{2^2}}},...,{R_n} = \frac{R}{{{2^{n - 1}}}},...\) có diện tích lần lượt là \({u_1},{u_2},{u_3},...,{u_n},...\) Ta có:
\(\begin{array}{l}{u_1} = \pi R_1^2 = \pi {R^2},{u_2} = \pi R_2^2 = \pi {\left( {\frac{R}{2}} \right)^2} = \pi {R^2}.\frac{1}{{{2^2}}},{u_3} = \pi R_3^2 = \pi {\left( {\frac{R}{{{2^2}}}} \right)^2} = \pi {R^2}.\frac{1}{{{2^4}}},...,\\{u_n} = \pi R_n^2 = \pi {\left( {\frac{R}{{{2^{n - 1}}}}} \right)^2} = \pi {R^2}.\frac{1}{{{2^{2n - 2}}}},...\end{array}\)
\(\begin{array}{l}S = {u_1} + {u_2} + ... + {u_n} + ... = \pi {R^2} + 2\pi {R^2}.\frac{1}{{{2^2}}} + 4.\pi {R^2}.\frac{1}{{{2^4}}} + ... + {2^{n + 1}}\pi {R^2}.\frac{1}{{{2^{2n - 2}}}} + ...\\\,\,\,\, = \pi {R^2} + \pi {R^2}.\frac{1}{2} + \pi {R^2}.\frac{1}{{{2^2}}} + ... + \pi {R^2}.\frac{1}{{{2^{n - 1}}}} + ...\\\,\,\,\, = \pi {R^2}\left( {1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{n - 1}}}} + ...} \right)\end{array}\)
Xét tổng: \({S_n} = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{n - 1}}}} + ...\)
Tổng trên là tổng của cấp số nhân lùi vô hạn có số hạng đầu \({u_1} = 1\) và công bội \(q = \frac{1}{2}\) nên: \({S_n} = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{n - 1}}}} + ... = \frac{1}{{1 - \frac{1}{2}}} = 2\).
Vậy \(S = \pi {R^2}.{S_n} = 2\pi {R^2}\).
Giải mục 3 trang 67, 68 SGK Toán 11 tập 1 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu
Mục 3 trong SGK Toán 11 tập 1 Chân trời sáng tạo thường xoay quanh các chủ đề về hàm số bậc hai, bao gồm định nghĩa, tính chất, đồ thị và ứng dụng. Việc nắm vững kiến thức này là nền tảng quan trọng cho các chương trình học tiếp theo. Bài viết này sẽ cung cấp hướng dẫn chi tiết từng bước để giải các bài tập trong mục này, giúp bạn tự tin hơn trong quá trình học tập.
Nội dung chính của Mục 3 trang 67, 68
- Định nghĩa hàm số bậc hai: Hàm số bậc hai có dạng y = ax² + bx + c, với a ≠ 0.
- Tính chất của hàm số bậc hai: Xác định đỉnh, trục đối xứng, khoảng đồng biến, nghịch biến.
- Đồ thị hàm số bậc hai (Parabol): Vẽ parabol, xác định các yếu tố quan trọng như đỉnh, trục đối xứng, giao điểm với trục tọa độ.
- Ứng dụng của hàm số bậc hai: Giải các bài toán thực tế liên quan đến quỹ đạo vật thể, tối ưu hóa diện tích, v.v.
Giải chi tiết các bài tập trong Mục 3 trang 67, 68
Chúng ta sẽ đi vào giải chi tiết từng bài tập trong mục này. Lưu ý rằng, việc hiểu rõ lý thuyết là yếu tố then chốt để giải bài tập thành công. Hãy đọc kỹ đề bài, xác định các thông tin đã cho và yêu cầu của bài toán. Sau đó, áp dụng các công thức và phương pháp phù hợp để tìm ra lời giải.
Bài 1: Xác định hệ số a, b, c của hàm số y = 2x² - 5x + 3
Đây là một bài tập cơ bản để kiểm tra khả năng nhận biết các hệ số của hàm số bậc hai. Hệ số a = 2, b = -5, c = 3.
Bài 2: Tìm đỉnh của parabol y = x² - 4x + 3
Để tìm đỉnh của parabol, ta sử dụng công thức: xđỉnh = -b / 2a và yđỉnh = f(xđỉnh). Trong trường hợp này, a = 1, b = -4, c = 3. Vậy xđỉnh = -(-4) / (2*1) = 2 và yđỉnh = 2² - 4*2 + 3 = -1. Vậy đỉnh của parabol là (2, -1).
Bài 3: Vẽ đồ thị hàm số y = -x² + 2x + 1
Để vẽ đồ thị, ta thực hiện các bước sau:
- Xác định đỉnh: xđỉnh = -b / 2a = -2 / (2*-1) = 1; yđỉnh = -1² + 2*1 + 1 = 2. Vậy đỉnh là (1, 2).
- Xác định trục đối xứng: x = 1.
- Xác định các điểm đặc biệt: Giao điểm với trục Oy (x = 0) là (0, 1). Giao điểm với trục Ox (y = 0) giải phương trình -x² + 2x + 1 = 0, ta được x = 1 ± √2. Vậy giao điểm là (1 + √2, 0) và (1 - √2, 0).
- Vẽ parabol đi qua các điểm đã xác định.
Mẹo học tập hiệu quả
- Nắm vững lý thuyết: Hiểu rõ định nghĩa, tính chất và các công thức liên quan.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng.
- Sử dụng các công cụ hỗ trợ: Máy tính bỏ túi, phần mềm vẽ đồ thị có thể giúp bạn giải quyết bài tập nhanh chóng và chính xác hơn.
- Hỏi thầy cô hoặc bạn bè: Nếu gặp khó khăn, đừng ngần ngại hỏi sự giúp đỡ.
Kết luận
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải các bài tập trong Mục 3 trang 67, 68 SGK Toán 11 tập 1 Chân trời sáng tạo. Chúc bạn học tập tốt và đạt kết quả cao!