Giải mục 2 trang 114, 115 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 2 trang 114, 115 SGK Toán 11 tập 1 - Chân trời sáng tạo
Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 114, 115 SGK Toán 11 tập 1 chương trình Chân trời sáng tạo. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Bài tập này thuộc chương trình học Toán 11, tập trung vào các kiến thức về...
Cho mặt phẳng (left( P right)) chứa hai đường thẳng (a,b) cắt nhau và cùng song song với mặt phẳng (left( Q right)). Giả sử (left( P right)) và (left( Q right)) có điểm chung (M) thì (left( P right)) cắt (left( Q right)) theo giao tuyến (c) (Hình 5).
Hoạt động 2
Cho mặt phẳng \(\left( P \right)\) chứa hai đường thẳng \(a,b\) cắt nhau và cùng song song với mặt phẳng \(\left( Q \right)\). Giả sử \(\left( P \right)\) và \(\left( Q \right)\) có điểm chung \(M\) thì \(\left( P \right)\) cắt \(\left( Q \right)\) theo giao tuyến \(c\) (Hình 5).
a) Giải thích tại sao đường thẳng \(c\) phải cắt ít nhất một trong hai đường thẳng \(a,b\). Điều này có trái với giả thiết \(a\) và \(b\) cùng song song với \(\left( Q \right)\) không?
b) Rút ra kết luận về số điểm chung và vị trí tương đối của \(\left( P \right)\) và \(\left( Q \right)\).
Phương pháp giải:
Sử dụng định lí:
‒ Cho đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\). Nếu mặt phẳng \(\left( Q \right)\) chứa \(a\), cắt \(\left( P \right)\) theo giao tuyến \(b\) thì \(a\) song song với \(b\).
‒ Trong không gian, qua một điểm nằm ngoài một đường thẳng, có một và chỉ một đường thẳng song song với đường thẳng đó.
‒ Đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\) nếu chúng không có điểm chung.
Lời giải chi tiết:
a) Gọi \(I\) là giao điểm của \(a\) và \(b\).
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}a\parallel \left( Q \right)\\\left( P \right) \supset a\\\left( P \right) \cap \left( Q \right) = c\end{array} \right\} \Rightarrow c\parallel a\\\left. \begin{array}{l}b\parallel \left( Q \right)\\\left( P \right) \supset b\\\left( P \right) \cap \left( Q \right) = c\end{array} \right\} \Rightarrow c\parallel b\end{array}\)
Do đó qua \(I\) ta kẻ được hai đường thẳng \(a\) và \(b\) cùng song song với \(c\), mâu thuẫn với định lí qua một điểm nằm ngoài một đường thẳng, có một và chỉ một đường thẳng song song với đường thẳng đó.
Vậy \(c\) phải cắt ít nhất một trong hai đường thẳng \(a,b\).
Nếu đường thẳng \(c\) cắt đường thẳng \(a\) hoặc đường thẳng \(b\), mà đường thẳng \(c\) nằm trong mặt phẳng \(\left( Q \right)\), khi đó đường thẳng \(a\) hoặc đường thẳng \(b\) có 1 điểm chung với mặt phẳng \(\left( Q \right)\). Điều này trái với giả thiết \(a\) và \(b\) cùng song song với \(\left( Q \right)\).
b) Vì \(\left( P \right)\) chứa đường thẳng \(a\) mà \(a\) song song với mặt phẳng \(\left( Q \right)\) nên \(\left( P \right)\) và \(\left( Q \right)\) là hai mặt phẳng phân biệt.
Theo chứng minh ở trên, nếu \(\left( P \right)\) và \(\left( Q \right)\) có điểm chung \(M\) thì mâu thuẫn với giả thiết \(a\) và \(b\) cùng song song với \(\left( Q \right)\).
Vậy hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) không có điểm chung.
Thực hành 1
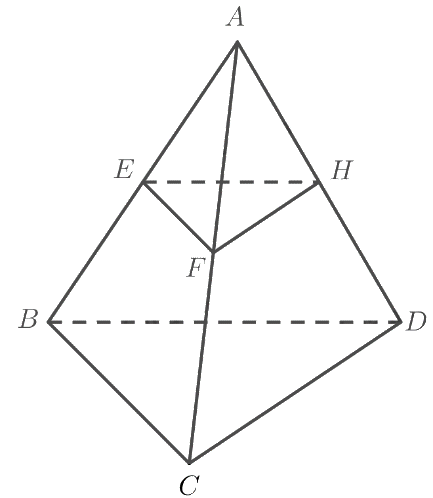
Cho tứ diện \(ABCD\) có \(E,F,H\)lần lượt là trung điểm của \(AB,AC,AD\). Chứng minh \(\left( {EFH} \right)\parallel \left( {BCD} \right)\).
Phương pháp giải:
Sử dụng định lí 1: Nếu mặt phẳng \(\left( P \right)\) chứa hai đường thẳng \(a,b\) cắt nhau và hai đường thẳng đó cùng song song với mặt phẳng \(\left( Q \right)\) thì \(\left( P \right)\) song song với \(\left( Q \right)\).
Lời giải chi tiết:

Ta có: \(E\) là trung điểm của \(AB\)
\(F\) là trung điểm của \(AC\)
\( \Rightarrow EF\) là đường trung bình của tam giác \(ABC\)
\(\left. \begin{array}{l} \Rightarrow EF\parallel BC\\BC \subset \left( {BC{\rm{D}}} \right)\end{array} \right\} \Rightarrow EF\parallel \left( {BC{\rm{D}}} \right)\)
\(E\) là trung điểm của \(AB\)
\(H\) là trung điểm của \(AD\)
\( \Rightarrow EH\) là đường trung bình của tam giác \(ABD\)
\(\left. \begin{array}{l} \Rightarrow EH\parallel BD\\BD \subset \left( {BC{\rm{D}}} \right)\end{array} \right\} \Rightarrow EH\parallel \left( {BC{\rm{D}}} \right)\)
Ta có:
\(\left. \begin{array}{l}EF\parallel \left( {BCD} \right)\\EH\parallel \left( {BCD} \right)\\EF,EH \subset \left( {EFH} \right)\end{array} \right\} \Rightarrow \left( {EFH} \right)\parallel \left( {BCD} \right)\)
Giải mục 2 trang 114, 115 SGK Toán 11 tập 1 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu
Mục 2 trang 114, 115 SGK Toán 11 tập 1 Chân trời sáng tạo là một phần quan trọng trong chương trình học, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế. Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho từng bài tập, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình làm bài.
Nội dung chính của Mục 2 trang 114, 115
Mục 2 này thường xoay quanh các chủ đề sau:
- Các khái niệm cơ bản: Ôn lại các định nghĩa, tính chất quan trọng liên quan đến...
- Ứng dụng của kiến thức: Giải các bài toán liên quan đến...
- Bài tập trắc nghiệm và tự luận: Rèn luyện kỹ năng giải quyết vấn đề thông qua các dạng bài tập khác nhau.
Giải chi tiết bài tập 1 (Ví dụ)
Đề bài: ... (Nội dung bài tập 1)
Lời giải:
- Bước 1: ...
- Bước 2: ...
- Bước 3: ...
Kết luận: ...
Giải chi tiết bài tập 2 (Ví dụ)
Đề bài: ... (Nội dung bài tập 2)
Lời giải:
... (Lời giải bài tập 2)
Mẹo giải bài tập hiệu quả
Để giải các bài tập trong Mục 2 trang 114, 115 SGK Toán 11 tập 1 Chân trời sáng tạo một cách hiệu quả, các em nên:
- Đọc kỹ đề bài và xác định rõ yêu cầu.
- Vận dụng các kiến thức đã học một cách linh hoạt.
- Kiểm tra lại kết quả sau khi giải xong.
- Tham khảo lời giải chi tiết trên Tusach.vn để hiểu rõ hơn về cách giải.
Bảng tổng hợp công thức liên quan
| Công thức | Mô tả |
|---|---|
| Công thức 1 | ... |
| Công thức 2 | ... |
Tusach.vn – Đồng hành cùng các em học Toán 11
Tusach.vn là website cung cấp tài liệu học tập trực tuyến uy tín, với đội ngũ giáo viên giàu kinh nghiệm và nội dung được cập nhật thường xuyên. Chúng tôi cam kết mang đến cho các em những trải nghiệm học tập tốt nhất.
Hãy truy cập Tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác và cùng chúng tôi chinh phục những thử thách trong môn Toán 11!
Lưu ý: Lời giải trên chỉ mang tính chất tham khảo. Các em nên tự mình giải bài tập để hiểu rõ hơn về kiến thức và rèn luyện kỹ năng giải quyết vấn đề.