Giải mục 1 trang 100, 101, 102 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 1 trang 100, 101, 102 SGK Toán 11 tập 1 - Chân trời sáng tạo
Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 100, 101, 102 sách giáo khoa Toán 11 tập 1 chương trình Chân trời sáng tạo. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Bài học này tập trung vào các kiến thức quan trọng về...
a) Nếu các trường hợp có thể xảy ra đối với hai đường thẳng \(a,b\) cùng nằm trong một mặt phẳng.
Hoạt động 1
a) Nếu các trường hợp có thể xảy ra đối với hai đường thẳng \(a,b\) cùng nằm trong một mặt phẳng.

b) Cho tứ diện \(ABCD\). Hai đường thẳng \(AB\) và \(CD\) có cùng nằm trong bất kì mặt phẳng nào không?
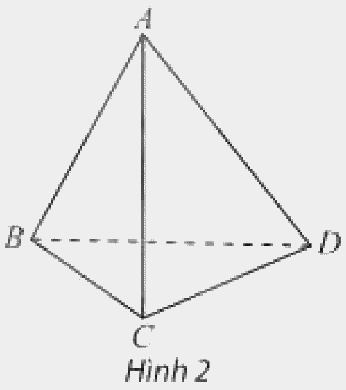
Phương pháp giải:
Quan sát hình ảnh, dựa vào vị trí tương đối của hai đường thẳng trong mặt phẳng.
Lời giải chi tiết:
a) Khi hai đường thẳng \(a,b\) cùng nằm trong một mặt phẳng thì:
‒ Nếu \(a,b\) có vô số điểm chung: Hai đường thẳng \(a,b\) trùng nhau.
‒ Nếu \(a,b\) có duy nhất một điểm chung: Hai đường thẳng \(a,b\) cắt nhau.
‒ Nếu \(a,b\) không có điểm chung: Hai đường thẳng \(a,b\) song song với nhau.
b) Hai đường thẳng \(AB\) và \(CD\) không cùng nằm trong bất kì mặt phẳng nào.
Thực hành 1
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Xét vị trí tương đối của các cặp đường thẳng sau đây:
a) \(AB\) và \(CD\);
b) \(SA\) và \(SC\);
c) \(SA\) và \(BC\).

Phương pháp giải:
Dựa vào vị trí tương đối của hai đường thẳng trong không gian:
• Trường hợp 1: Có một mặt phẳng chứa \(a\) và \(b\). Khi đó ta nói \(a\) và \(b\) đồng phẳng. Theo kết quả của hình học phẳng, có ba khả năng sau đây xảy ra:
‒ Nếu \(a\) và \(b\) có hai điểm chung thì ta nói \(a\) trùng \(b\).
‒ Nếu \(a\) và \(b\) có một điểm chung duy nhất M thì ta nói \(a\) và \(b\) cắt nhau tại M.
‒ Nếu \(a\) và \(b\) không có điểm chung thì ta nói \(a\) và \(b\) song song với nhau.
• Trường hợp 2: Không có mặt phẳng nào chứa cả \(a\) và \(b\). Khi đó ta nói hai đường thẳng \(a\) và \(b\) chéo nhau hay \(a\) chéo với \(b\).
Lời giải chi tiết:
a) \(AB\) và \(CD\) cùng nằm trong mặt phẳng \(\left( {ABCD} \right)\).
\(ABCD\) là hình bình hành nên \(AB\parallel C{\rm{D}}\).
b) \(SA\) và \(SC\) cùng nằm trong mặt phẳng \(\left( {SAC} \right)\).
Do đó \(SA\) và \(SC\) cắt nhau tại \(S\).
c) Giả sử \(SA\) và \(BC\) cùng nằm trong mặt phẳng \(\left( P \right)\).
Suy ra đường thẳng \(AC\) cũng nằm trong \(\left( P \right)\).
Do đó \(\left( P \right)\) chứa cả 4 điểm của tứ diện \(SABC\) (vô lí do \(S\) không nằm trong mặt phẳng \(\left( {ABCD} \right)\)).
Vậy \(SA\) và \(BC\) không cùng nằm trong một mặt phẳng. Vậy \(SA\) và \(BC\) chéo nhau.
Vận dụng 1
Hãy chỉ ra các ví dụ về hai đường thẳng song song, cắt nhau và chéo nhau trong hình cầu sắt ở Hình 6.

Phương pháp giải:
Quan sát, dựa vào vị trí tương đối của hai đường thẳng trong không gian.
Lời giải chi tiết:
‒ Hai thanh sắt đối diện nhau ở hai bên cầu song song với nhau.
‒ Hai thanh sắt liền nhau cùng nằm ở thành cầu hoặc mái cầu cắt nhau.
‒ Thanh sắt nằm ở mái cầu và thanh sắt nằm ở thành cầu chéo nhau.
Giải mục 1 trang 100, 101, 102 SGK Toán 11 tập 1 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 1 trang 100, 101, 102 SGK Toán 11 tập 1 Chân trời sáng tạo là một phần quan trọng trong chương trình học, tập trung vào việc củng cố kiến thức về hàm số và đồ thị. Để giúp các em học sinh nắm vững kiến thức và tự tin giải bài tập, tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho từng bài tập trong mục này.
Nội dung chính của Mục 1
Mục 1 bao gồm các bài tập liên quan đến:
- Xác định tập xác định của hàm số.
- Tìm tập giá trị của hàm số.
- Kiểm tra tính chẵn, lẻ của hàm số.
- Vẽ đồ thị hàm số.
- Ứng dụng đồ thị hàm số để giải các bài toán thực tế.
Hướng dẫn giải chi tiết từng bài tập
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 1 trang 100, 101, 102 SGK Toán 11 tập 1 Chân trời sáng tạo:
Bài 1: (Trang 100)
Đề bài: ... (Nội dung bài tập)
Lời giải: ... (Giải thích chi tiết từng bước giải)
Bài 2: (Trang 101)
Đề bài: ... (Nội dung bài tập)
Lời giải: ... (Giải thích chi tiết từng bước giải)
Bài 3: (Trang 102)
Đề bài: ... (Nội dung bài tập)
Lời giải: ... (Giải thích chi tiết từng bước giải)
Mẹo giải bài tập hiệu quả
Để giải các bài tập về hàm số và đồ thị một cách hiệu quả, các em cần:
- Nắm vững định nghĩa và tính chất của các loại hàm số.
- Thực hành vẽ đồ thị hàm số thường gặp.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm vẽ đồ thị.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Ví dụ minh họa
Để hiểu rõ hơn về cách giải các bài tập trong mục 1, chúng ta cùng xem xét một ví dụ minh họa:
Ví dụ: Cho hàm số y = f(x) = x2 - 2x + 1. Hãy xác định tập xác định và tập giá trị của hàm số.
Lời giải:
- Tập xác định của hàm số là tập hợp tất cả các giá trị của x sao cho biểu thức f(x) có nghĩa. Trong trường hợp này, hàm số y = x2 - 2x + 1 là một hàm đa thức, do đó tập xác định của hàm số là tập số thực R.
- Tập giá trị của hàm số là tập hợp tất cả các giá trị của y mà hàm số có thể nhận được. Để tìm tập giá trị, ta có thể viết lại hàm số dưới dạng y = (x - 1)2. Vì (x - 1)2 luôn lớn hơn hoặc bằng 0, nên y ≥ 0. Do đó, tập giá trị của hàm số là [0, +∞).
Kết luận
Hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh đã có thể tự tin giải các bài tập trong mục 1 trang 100, 101, 102 SGK Toán 11 tập 1 Chân trời sáng tạo. Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với tusach.vn để được hỗ trợ nhé!
| Bài tập | Lời giải |
|---|---|
| Bài 1 (Trang 100) | Xem chi tiết tại tusach.vn |
| Bài 2 (Trang 101) | Xem chi tiết tại tusach.vn |
| Bài 3 (Trang 102) | Xem chi tiết tại tusach.vn |