Logo

Bài 12 trang 42 SGK Toán 11 tập 1 - Chân trời sáng tạo

Tổng quan nội dung

Bài 12 trang 42 SGK Toán 11 tập 1 - Chân trời sáng tạo

Bài 12 trang 42 SGK Toán 11 tập 1 thuộc chương trình Toán 11 Chân trời sáng tạo, tập trung vào việc ôn tập chương 1: Hàm số và đồ thị. Bài tập này yêu cầu học sinh vận dụng kiến thức về các loại hàm số, tính đơn điệu, cực trị và ứng dụng của đạo hàm để giải quyết các bài toán cụ thể.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.

Độ sâu h (m) của mực nước ở một cảng biển vào thời điểm t (giờ)

Đề bài

Độ sâu h (m) của mực nước ở một cảng biển vào thời điểm t (giờ) sau khi thuỷ triểu lên lần đầu tiên trong ngày được tính xấp xỉ bởi công thức \(h(t) = 0,8cos0,5t + 4.\)

(Theo https://noc.ac.uk/files/documents/business/an-introduction-to-tidal-modelling.pdf)

a) Độ sâu của nước vào thời điểm t = 2 là bao nhiêu mét?

b) Một con tàu cần mực nước sâu tối thiểu 3,6 m để có thể di chuyển ra vào cảng an toàn. Dựa vào đồ thị của hàm số côsin, hãy cho biết trong vòng 12 tiếng đầu tiên sau khi thuỷ triểu lên lần đầu tiên, ở những thời điểm t nào tàu có thể hạ thuỷ. Làm tròn kết quả đến hàng phần trăm.

Phương pháp giải - Xem chi tiếtBài 12 trang 42 SGK Toán 11 tập 1 - Chân trời sáng tạo 1

a) Thay t = 2 vào công thức h(t).

b) Giải phương trình côsin để tìm t.

Lời giải chi tiết

a) Tại thời điểm t = 2 độ sâu của nước là: \(h\left( 2 \right) = 0,8cos0,5.2 + 4 \approx 4,43{\rm{ }}m.\)

Vậy độ sâu của nước ở thời điểm t = 2 là khoảng 4,43 m.

b) Các thời điểm để mực nước sâu là 3,6m tương ứng với phương trình \(0,8cos0,5t + 4 = 3,6\).

Ta có: \(0,8cos0,5t + 4 = 3,6\)

\(\begin{array}{l} \Leftrightarrow cos0,5t = - \frac{1}{2} = cos\frac{{2\pi }}{3}\\ \Leftrightarrow 0,5t = \pm \frac{{2\pi }}{3} + k2\pi ,k \in \mathbb{Z}\\ \Leftrightarrow t = \pm \frac{{4\pi }}{3} + k4\pi ,k \in \mathbb{Z}\end{array}\)

Với \(t = \frac{{4\pi }}{3} + k4\pi \), trong 12 tiếng ta có các thời điểm \(0 \le \frac{{4\pi }}{3} + k4\pi \le 12 \Leftrightarrow - 0,3 \le k \le 0,62 \Rightarrow k = 0 \Rightarrow t = \frac{{4\pi }}{3}\).

Với \(t = - \frac{{4\pi }}{3} + k4\pi \), trong 12 tiếng ta có các thời điểm \(0 \le - \frac{{4\pi }}{3} + k4\pi \le 12 \Leftrightarrow 0,3 \le k \le 1,28 \Rightarrow k = 1 \Rightarrow t = - \frac{{4\pi }}{3} + 4\pi = \frac{{8\pi }}{3}\).

Hai thời điểm t vừa tìm được chính là giao điểm của đồ thị h(t) với đường thẳng y = 3,6.

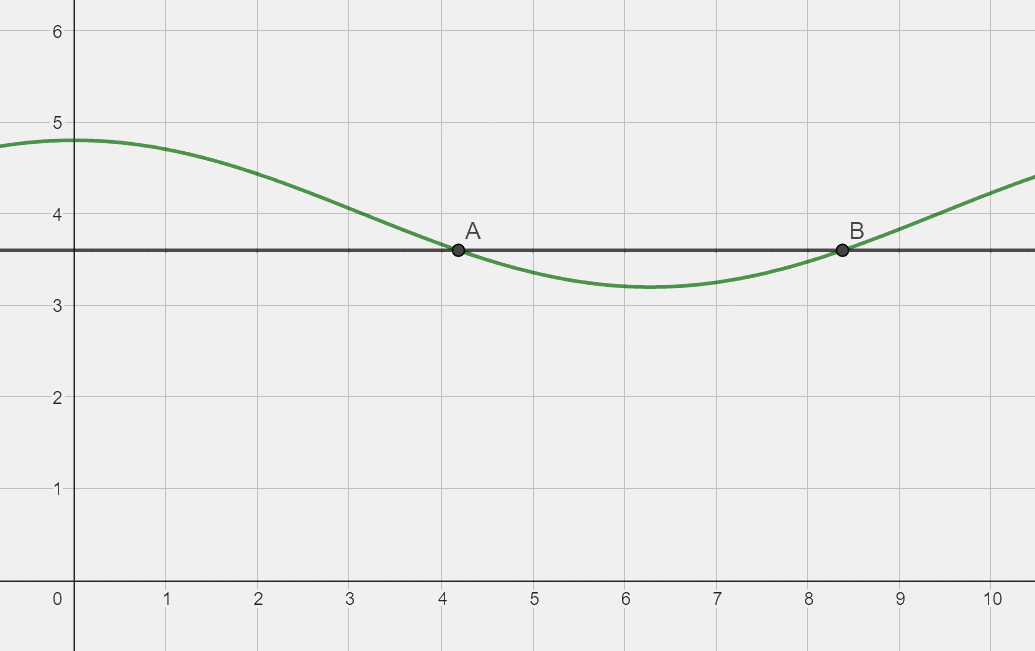
Bài 12 trang 42 SGK Toán 11 tập 1 - Chân trời sáng tạo 2

Ta thấy trong khoảng \(\left( {\frac{{4\pi }}{3};\frac{{8\pi }}{3}} \right)\), đồ thị h(t) nằm dưới đường thẳng y = 3,6, tức trong khoảng thời gian t đó, mực nước thấp hơn 3,6 m và tàu không thể hạ thủy.

Vậy tàu có thể hạ thủy vào các thời điểm \(t\in \left[ 0;\frac{4\pi }{3} \right]\cup \left[ \frac{8\pi }{3};12 \right]\).

Bài 12 Trang 42 SGK Toán 11 Tập 1 - Chân Trời Sáng Tạo: Giải Chi Tiết và Hướng Dẫn

Bài 12 trang 42 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình ôn tập chương 1. Bài tập này giúp học sinh củng cố kiến thức về hàm số, đồ thị hàm số, và các ứng dụng của đạo hàm. Dưới đây là giải chi tiết từng phần của bài tập, cùng với những lưu ý quan trọng để học sinh có thể tự tin giải quyết các bài toán tương tự.

Nội dung bài tập

Bài 12 thường bao gồm các dạng bài tập sau:

  • Xác định tính đơn điệu của hàm số.
  • Tìm cực trị của hàm số.
  • Vẽ đồ thị hàm số.
  • Giải các bài toán ứng dụng liên quan đến hàm số.

Giải chi tiết bài tập

Để giải bài tập này, chúng ta cần nắm vững các kiến thức sau:

  1. Định nghĩa hàm số: Hiểu rõ khái niệm hàm số, tập xác định, tập giá trị.
  2. Các loại hàm số: Hàm số bậc nhất, hàm số bậc hai, hàm số mũ, hàm số logarit, hàm số lượng giác.
  3. Đạo hàm: Tính đạo hàm của hàm số, ý nghĩa của đạo hàm.
  4. Tính đơn điệu của hàm số: Sử dụng đạo hàm để xét tính đơn điệu của hàm số.
  5. Cực trị của hàm số: Tìm cực đại, cực tiểu của hàm số.

Ví dụ, xét hàm số y = x3 - 3x2 + 2. Để tìm cực trị của hàm số, ta thực hiện các bước sau:

  1. Tính đạo hàm y' = 3x2 - 6x.
  2. Giải phương trình y' = 0 để tìm các điểm cực trị: 3x2 - 6x = 0 => x = 0 hoặc x = 2.
  3. Xét dấu của đạo hàm y' trên các khoảng xác định để xác định loại cực trị:
    • Khi x < 0, y' > 0 => Hàm số đồng biến.
    • Khi 0 < x < 2, y' < 0 => Hàm số nghịch biến.
    • Khi x > 2, y' > 0 => Hàm số đồng biến.
  4. Kết luận: Hàm số đạt cực đại tại x = 0, giá trị cực đại là y = 2. Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là y = -2.

Lưu ý khi giải bài tập

Khi giải bài tập về hàm số, cần lưu ý những điều sau:

  • Đọc kỹ đề bài, xác định rõ yêu cầu của bài toán.
  • Sử dụng đúng các công thức và định lý.
  • Kiểm tra lại kết quả sau khi giải xong.
  • Rèn luyện thường xuyên để nắm vững kiến thức và kỹ năng.

Ứng dụng của bài tập

Việc giải bài tập về hàm số có nhiều ứng dụng trong thực tế, chẳng hạn như:

  • Dự đoán xu hướng phát triển của các hiện tượng kinh tế, xã hội.
  • Tối ưu hóa các quy trình sản xuất, kinh doanh.
  • Phân tích dữ liệu và đưa ra các quyết định chính xác.

tusach.vn hy vọng với lời giải chi tiết và hướng dẫn trên, các bạn học sinh sẽ hiểu rõ hơn về Bài 12 trang 42 SGK Toán 11 tập 1 - Chân trời sáng tạo và tự tin giải quyết các bài toán tương tự. Chúc các bạn học tốt!