Giải mục 4 trang 69, 70, 71 SGK Toán 11 tập 2 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 4 trang 69, 70, 71 SGK Toán 11 tập 2 - Chân trời sáng tạo
Chào mừng các em học sinh đến với lời giải chi tiết mục 4 trang 69, 70, 71 SGK Toán 11 tập 2 - Chân trời sáng tạo. Bài viết này sẽ cung cấp đáp án và hướng dẫn giải các bài tập trong mục, giúp các em hiểu rõ kiến thức và rèn luyện kỹ năng giải toán.
tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
a) Cho hình lăng trụ (ABCDE.A'B'C'D'E') có cạnh bên (AA') vuông góc với một mặt phẳng đáy (Hình 18a). Có nhận xét gì về các mặt bên của hình lăng trụ này?
Hoạt động 6
a) Cho hình lăng trụ \(ABCDE.A'B'C'D'E'\) có cạnh bên \(AA'\) vuông góc với một mặt phẳng đáy (Hình 18a). Có nhận xét gì về các mặt bên của hình lăng trụ này?
b) Cho hình lăng trụ có đáy là đa giác đều và có cạnh bên vuông góc với một mặt phẳng đáy (Hình 18b). Có nhận xét gì các mặt bên của hình lăng trụ này?
c) Một hình lăng trụ nếu có đây là hình bình hành và có cạnh bên vuông góc với mặt phẳng đáy (Hình 18c) thì có bao nhiêu mặt là hình chữ nhật?
d) Một hình hộp nếu có đáy là hình chữ nhật và có cạnh bên vuông góc với mặt phẳng đáy (Hinh 18d) thì có bao nhiêu mặt là hình chữ nhật?
Phương pháp giải:
Quan sát hình ảnh và trả lời câu hỏi.
Lời giải chi tiết:
a) Các mặt bên của hình lăng trụ này là hình chữ nhật vuông góc với mặt phẳng đáy.
b) Các mặt bên của hình lăng trụ này là hình chữ nhật vuông góc với mặt phẳng đáy.
c) Hình lăng trụ đó có 4 mặt bên là hình chữ nhật.
d) Hình lăng trụ đó có cả 6 mặt là hình chữ nhật.
Thực hành 3
Cho hình lăng trụ lục giác đều \(ABCDEF.A'B'C'D'E'F'\) có cạnh bên bằng \(h\) và cạnh đáy bằng \(a\). Tính \(A'C\) và \(A'D\) theo \(a\) và \(h\).
Phương pháp giải:
Sử dụng phép chiếu vuông góc.
Lời giải chi tiết:

Tam giác \(ABC\) có:
\(AC = \sqrt {A{B^2} + B{C^2} - 2.AB.BC.\cos \widehat {ABC}} = a\sqrt 3 \)
\(AA' \bot \left( {ABC{\rm{DEF}}} \right) \Rightarrow AA' \bot AC\)
\( \Rightarrow \Delta AA'C\) vuông tại \(A\)
\( \Rightarrow A'C = \sqrt {AA{'^2} + A{C^2}} = \sqrt {{h^2} + 3{{\rm{a}}^2}} \).
Gọi \(O\) là tâm lục giác đều \(ABC{\rm{DEF}}\).
\(\Delta OAB,\Delta OC{\rm{D}}\) đều \( \Rightarrow OA = O{\rm{D}} = AB = a \Rightarrow A{\rm{D}} = 2a\)
\(AA' \bot \left( {ABC{\rm{DEF}}} \right) \Rightarrow AA' \bot AD\)
\( \Rightarrow \Delta AA'D\) vuông tại \(A\)
\( \Rightarrow A'D = \sqrt {AA{'^2} + A{D^2}} = \sqrt {{h^2} + 4{{\rm{a}}^2}} \).
Vận dụng 3
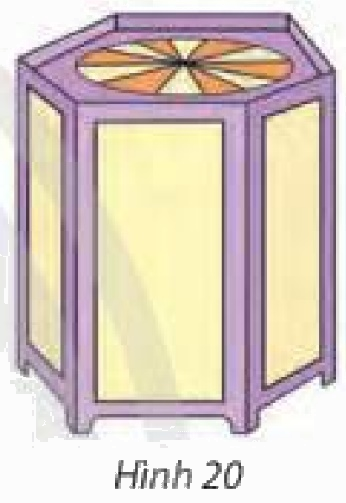
Một chiếc lồng đèn kéo quân có dạng hình lăng trụ lục giác đều với cạnh đáy bằng 10 cm và cạnh bên bằng 30 cm (Hình 20). Tính tổng diện tích các mặt bên của chiếc lồng đèn đó.

Phương pháp giải:
Tính diện tích 1 mặt. Tổng diện tích các mặt bên bằng 6 lần diện tích 1 mặt.
Lời giải chi tiết:
Diện tích một mặt bên của lồng đèn là: \(10.30 = 300\left( {c{m^2}} \right)\)
Tổng diện tích các mặt bên của chiếc lồng đèn đó là: \(300.6 = 1800\left( {c{m^2}} \right)\)
Giải mục 4 trang 69, 70, 71 SGK Toán 11 tập 2 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 4 trong SGK Toán 11 tập 2 - Chân trời sáng tạo tập trung vào các kiến thức về đường thẳng và mặt phẳng trong không gian. Đây là một phần quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững các khái niệm, định lý và phương pháp giải bài tập liên quan. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập trong mục 4, trang 69, 70, 71, giúp các em hiểu rõ hơn về nội dung bài học và tự tin giải các bài tập tương tự.
Nội dung chính của Mục 4
- Khái niệm về đường thẳng và mặt phẳng trong không gian: Định nghĩa, các tính chất cơ bản.
- Quan hệ giữa đường thẳng và mặt phẳng: Đường thẳng song song với mặt phẳng, đường thẳng nằm trong mặt phẳng, đường thẳng cắt mặt phẳng.
- Hai mặt phẳng song song: Điều kiện để hai mặt phẳng song song, các tính chất.
- Góc giữa đường thẳng và mặt phẳng: Định nghĩa, cách tính góc.
- Khoảng cách từ một điểm đến mặt phẳng: Công thức tính khoảng cách.
Giải chi tiết các bài tập trang 69, 70, 71
Bài 1 (Trang 69):
Đề bài: Cho hình chóp S.ABCD. Gọi M là trung điểm của cạnh BC. Chứng minh rằng AM song song với mặt phẳng (SCD).
Lời giải:
- Gọi N là trung điểm của cạnh CD.
- Chứng minh MN song song với SD (sử dụng định lý Thales).
- Vì MN song song với SD và MN nằm trong mặt phẳng (AMN), SD nằm trong mặt phẳng (SCD) nên (AMN) song song với (SCD).
- Do AM nằm trong mặt phẳng (AMN) nên AM song song với mặt phẳng (SCD).
Bài 2 (Trang 70):
Đề bài: Cho hình chóp S.ABCD. Gọi H là hình chiếu vuông góc của S lên mặt phẳng (ABCD). Chứng minh rằng nếu SA = SB = SC = SD thì SH vuông góc với (ABCD).
Lời giải:
Bài này sử dụng kiến thức về tính chất đường vuông góc và đường xiên. (Giải thích chi tiết các bước chứng minh, sử dụng các định lý liên quan).
Bài 3 (Trang 71):
Đề bài: Tính khoảng cách từ điểm A đến mặt phẳng (BCD) trong hình chóp S.ABCD, biết rằng... (giả thiết cụ thể của bài toán).
Lời giải:
(Giải chi tiết bài toán, sử dụng công thức tính khoảng cách từ một điểm đến mặt phẳng).
Mẹo học tốt Toán 11 - Chương Đường thẳng và mặt phẳng trong không gian
- Nắm vững định nghĩa và tính chất: Đây là nền tảng để giải quyết mọi bài tập.
- Vẽ hình: Hình vẽ trực quan giúp bạn hiểu rõ hơn về bài toán và tìm ra hướng giải quyết.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau sẽ giúp bạn rèn luyện kỹ năng và làm quen với các dạng bài.
- Sử dụng tài liệu tham khảo: Sách giáo khoa, sách bài tập, các trang web học toán trực tuyến là những nguồn tài liệu hữu ích.
tusach.vn hy vọng với lời giải chi tiết và hướng dẫn trên, các em sẽ học tốt môn Toán 11 và đạt kết quả cao trong các kỳ thi. Chúc các em thành công!