Bài 3 trang 127 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Bài 3 trang 127 SGK Toán 11 Tập 1 - Chân trời sáng tạo
Bài 3 thuộc chương trình học Toán 11 Tập 1, sách Chân trời sáng tạo, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến phép biến hóa lượng giác. Bài tập này giúp học sinh củng cố kiến thức về công thức lượng giác và áp dụng vào giải quyết các bài toán thực tế.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
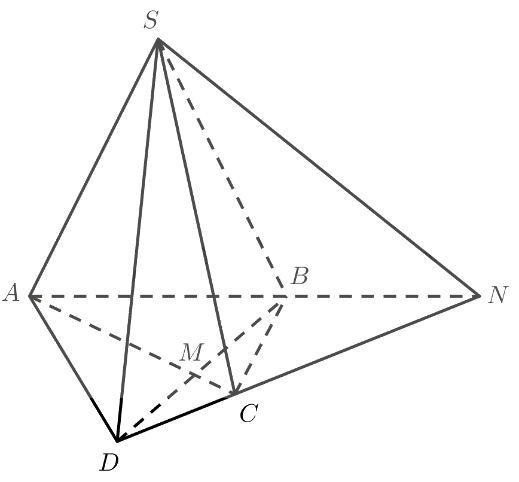
Cho hình chóp \(S.ABCD\) có \(AC\) cắt \(B{\rm{D}}\) tại \(M\), \(AB\) cắt \(C{\rm{D}}\) tại \(N\). Trong các đường thẳng sau đây, đường nào là giao tuyến của \(\left( {SAC} \right)\) và \(\left( {SBD} \right)\)?
Đề bài
Cho hình chóp \(S.ABCD\) có \(AC\) cắt \(B{\rm{D}}\) tại \(M\), \(AB\) cắt \(C{\rm{D}}\) tại \(N\). Trong các đường thẳng sau đây, đường nào là giao tuyến của \(\left( {SAC} \right)\) và \(\left( {SBD} \right)\)?
A. \(SM\).
B. \(SN\).
C. \(SB\).
D. \(SC\).
Phương pháp giải - Xem chi tiết
Để tìm giao tuyến của hai mặt phẳng, ta tìm hai điểm chung phân biệt của hai mặt phẳng đó.
Lời giải chi tiết
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}S \in \left( {SAC} \right)\\S \in \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow S \in \left( {SAC} \right) \cap \left( {SB{\rm{D}}} \right)\\\left. \begin{array}{l}M \in AC \subset \left( {SAC} \right)\\M \in B{\rm{D}} \subset \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow M \in \left( {SAC} \right) \cap \left( {SB{\rm{D}}} \right)\end{array}\)
Vậy giao tuyến của hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SBD} \right)\) là đường thẳng \(SM\).
Chọn A.
Bài 3 trang 127 SGK Toán 11 Tập 1 - Chân trời sáng tạo: Giải chi tiết và hướng dẫn
Bài 3 trang 127 SGK Toán 11 Tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học, giúp học sinh rèn luyện kỹ năng giải các bài toán liên quan đến phép biến hóa lượng giác. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này, được cung cấp bởi tusach.vn.
Nội dung bài tập
Bài 3 yêu cầu học sinh thực hiện các phép biến đổi lượng giác để rút gọn biểu thức hoặc chứng minh đẳng thức. Bài tập thường bao gồm các công thức lượng giác cơ bản như công thức cộng, trừ, nhân, chia góc, công thức hạ bậc, nâng bậc, và các công thức biến đổi khác.
Lời giải chi tiết
Để giải bài tập này, học sinh cần nắm vững các công thức lượng giác và biết cách áp dụng chúng một cách linh hoạt. Dưới đây là một ví dụ về cách giải một dạng bài tập thường gặp:
Ví dụ: Rút gọn biểu thức A = sin2x + cos2x + 2sin x cos x
- Áp dụng công thức sin2x + cos2x = 1
- Áp dụng công thức sin 2x = 2sin x cos x
- Thay thế vào biểu thức A, ta được: A = 1 + sin 2x
Như vậy, biểu thức A đã được rút gọn thành 1 + sin 2x.
Các dạng bài tập thường gặp
- Rút gọn biểu thức lượng giác
- Chứng minh đẳng thức lượng giác
- Giải phương trình lượng giác
- Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức lượng giác
Mẹo giải bài tập
Để giải bài tập về phép biến hóa lượng giác một cách hiệu quả, học sinh nên:
- Nắm vững các công thức lượng giác cơ bản
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau
- Sử dụng các công thức biến đổi một cách linh hoạt
- Kiểm tra lại kết quả sau khi giải bài tập
Tài liệu tham khảo
Ngoài SGK Toán 11 Tập 1 - Chân trời sáng tạo, học sinh có thể tham khảo thêm các tài liệu sau:
- Sách bài tập Toán 11
- Các trang web học toán trực tuyến
- Các video hướng dẫn giải bài tập trên YouTube
Kết luận
Bài 3 trang 127 SGK Toán 11 Tập 1 - Chân trời sáng tạo là một bài tập quan trọng, giúp học sinh củng cố kiến thức về phép biến hóa lượng giác. Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trên đây, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.
tusach.vn luôn đồng hành cùng các em học sinh trên con đường chinh phục kiến thức. Hãy truy cập tusach.vn để xem thêm nhiều bài giải và tài liệu học tập hữu ích khác.
| Công thức | Mô tả |
|---|---|
| sin2x + cos2x = 1 | Đẳng thức lượng giác cơ bản |
| sin 2x = 2sin x cos x | Công thức góc đôi |