Giải mục 2 trang 9, 10 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 2 trang 9, 10 SGK Toán 11 tập 1 - Chân trời sáng tạo
Chào mừng bạn đến với tusach.vn! Chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong sách giáo khoa Toán 11 tập 1 Chân trời sáng tạo. Mục tiêu của chúng tôi là giúp bạn học tập hiệu quả và đạt kết quả tốt nhất.
Bài viết này sẽ tập trung vào việc giải các bài tập trong mục 2, trang 9 và 10 của SGK Toán 11 tập 1 Chân trời sáng tạo. Hãy cùng chúng tôi khám phá!
Vẽ đường tròn tâm O bán kính R bất kì. Dùng một đoạn dây mềm đo bán kính và đánh dấu được một cung AB có độ dài đúng bằng R (Hình 9).
Hoạt động 3
Vẽ đường tròn tâm O bán kính R bất kì. Dùng một đoạn dây mềm đo bán kính và đánh dấu được một cung AB có độ dài đúng bằng R (Hình 9). Đo và cho biết \(\widehat {AOB}\) có số đo bằng bao nhiêu độ.
Phương pháp giải:
Vẽ đường tròn và xác định góc như phía trên đã học
Lời giải chi tiết:
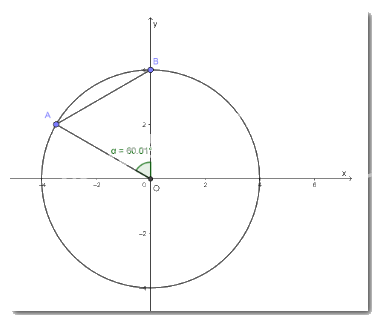
\( \Rightarrow \widehat {AOB} = 60^\circ \)
Thực hành 2
Hoàn thành bảng chuyển đổi đơn vị đo của các góc sau đây:
Số đo theo độ | 0° | ? | 45° | 60° | ? | 120° | ? | 150° | 180° |
Số đo theo rad | ? | \(\frac{\pi }{6}(rad)\) | ? | ? | \(\frac{\pi }{2}(rad)\) | ? | \(\frac{{3\pi }}{4}(rad)\) | ? | \(\pi (rad)\) |
Phương pháp giải:
Sử dụng công thức \({\alpha ^ \circ } = \frac{{\pi \alpha }}{{180}}\,\)rad ; \(\alpha \,\,rad = {\left( {\frac{{180\alpha }}{\pi }} \right)^0}\)
Lời giải chi tiết:
Số đo theo độ | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° |
Số đo theo rad | 0 | \(\frac{\pi }{6}(rad)\) | \(\frac{\pi }{4}\left( {rad} \right)\) | \(\frac{\pi }{3}\left( {rad} \right)\) | \(\frac{\pi }{2}(rad)\) | \[\frac{{2\pi }}{3}(rad)\] | \(\frac{{3\pi }}{4}(rad)\) | \(\frac{{5\pi }}{6}(rad)\) | \(\pi (rad)\) |
Giải mục 2 trang 9, 10 SGK Toán 11 tập 1 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu
Mục 2 của SGK Toán 11 tập 1 Chân trời sáng tạo tập trung vào các kiến thức cơ bản về hàm số bậc hai. Đây là một phần quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững các khái niệm và kỹ năng liên quan. Bài viết này sẽ cung cấp hướng dẫn chi tiết và dễ hiểu để giải các bài tập trong mục này, giúp bạn tự tin hơn trong quá trình học tập.
Nội dung chính của Mục 2
Trước khi đi vào giải bài tập, chúng ta cùng điểm qua những nội dung chính của Mục 2:
- Định nghĩa hàm số bậc hai
- Dạng tổng quát của hàm số bậc hai: y = ax2 + bx + c (a ≠ 0)
- Hệ số a, b, c và vai trò của chúng
- Đồ thị của hàm số bậc hai (Parabol)
- Đỉnh của Parabol
- Trục đối xứng của Parabol
- Bảng biến thiên của hàm số bậc hai
Giải bài tập trang 9 SGK Toán 11 tập 1 - Chân trời sáng tạo
Bài 1: Xác định hệ số a, b, c của các hàm số sau:
- y = 2x2 - 5x + 1
- y = -x2 + 3x
- y = 4x - x2 + 2
Lời giải:
- a = 2, b = -5, c = 1
- a = -1, b = 3, c = 0
- a = -1, b = 4, c = 2
Giải bài tập trang 10 SGK Toán 11 tập 1 - Chân trời sáng tạo
Bài 2: Vẽ đồ thị của hàm số y = x2 - 4x + 3
Lời giải:
- Xác định đỉnh của Parabol: xđỉnh = -b/2a = -(-4)/(2*1) = 2. yđỉnh = (2)2 - 4(2) + 3 = -1. Vậy đỉnh là (2, -1).
- Xác định trục đối xứng: x = 2
- Xác định các điểm đặc biệt:
- Giao điểm với trục Oy: x = 0 => y = 3. Điểm (0, 3)
- Giao điểm với trục Ox: y = 0 => x2 - 4x + 3 = 0 => (x-1)(x-3) = 0 => x = 1 hoặc x = 3. Điểm (1, 0) và (3, 0)
- Vẽ đồ thị Parabol đi qua các điểm đã xác định.
Mẹo giải bài tập hàm số bậc hai
Để giải các bài tập về hàm số bậc hai một cách hiệu quả, bạn nên:
- Nắm vững định nghĩa và các tính chất của hàm số bậc hai.
- Thực hành giải nhiều bài tập khác nhau để làm quen với các dạng bài.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm vẽ đồ thị.
- Kiểm tra lại kết quả sau khi giải xong.
Tài liệu tham khảo thêm
Ngoài SGK, bạn có thể tham khảo thêm các tài liệu sau để hiểu rõ hơn về hàm số bậc hai:
- Sách bài tập Toán 11
- Các trang web học Toán trực tuyến
- Video bài giảng trên YouTube
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích và giúp bạn giải quyết các bài tập trong mục 2 trang 9, 10 SGK Toán 11 tập 1 Chân trời sáng tạo một cách dễ dàng. Chúc bạn học tập tốt!