Bài 5 trang 127 Toán 11 Tập 1 - Chân trời sáng tạo

Bài 5 trang 127 SGK Toán 11 tập 1 - Chân trời sáng tạo

Bài 5 trang 127 SGK Toán 11 Tập 1 - Chân trời sáng tạo

Bài 5 thuộc chương trình Toán 11 Tập 1, sách Chân trời sáng tạo, tập trung vào việc ôn tập chương 1: Hàm số và đồ thị. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán liên quan đến hàm số bậc hai, đồ thị hàm số và ứng dụng của hàm số trong thực tế.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.

Cho hình bình hành \(ABCD\) và một điểm \(S\) không nằm trong mặt phẳng \(\left( {ABCD} \right)\). Giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\) là một đường thẳng song song với đường thẳng nào sau đây?

Đề bài

A. \(AB\).

B. \(AC\).

C. \(BC\).

D. \(SA\).

Phương pháp giải - Xem chi tiết Bài 5 trang 127 SGK Toán 11 tập 1 - Chân trời sáng tạo 1

Để tìm giao tuyến của hai mặt phẳng, tìm 1 điểm chung và 2 đường thẳng song song nằm trên mỗi mặt phẳng. Giao tuyến là đường thẳng đi qua điểm chung và song song với hai đường thẳng đó.

Lời giải chi tiết

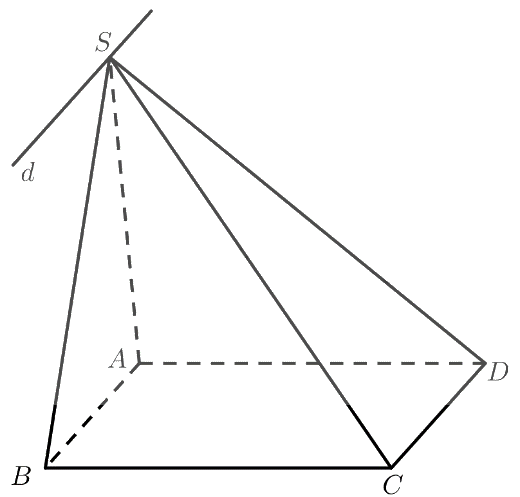
Bài 5 trang 127 SGK Toán 11 tập 1 - Chân trời sáng tạo 2

Ta có:

\(\left. \begin{array}{l}S \in \left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right)\\A{\rm{B}}\parallel C{\rm{D}}\\AB \subset \left( {SAB} \right)\\C{\rm{D}} \subset \left( {SC{\rm{D}}} \right)\end{array} \right\}\)

\( \Rightarrow \)Giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\) là đường thẳng \(d\) đi qua \(S\), song song với \(AB\) và \(C{\rm{D}}\).

Chọn A.

Bài 5 trang 127 SGK Toán 11 Tập 1 - Chân trời sáng tạo: Giải chi tiết và hướng dẫn

Bài 5 trang 127 SGK Toán 11 Tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về hàm số bậc hai và ứng dụng của nó. Dưới đây là giải chi tiết và hướng dẫn giải bài tập này:

Nội dung bài tập

Bài tập yêu cầu học sinh thực hiện các nhiệm vụ sau:

Xác định các hệ số a, b, c của hàm số bậc hai.
Tìm tọa độ đỉnh của parabol.
Vẽ đồ thị hàm số.
Xác định khoảng đồng biến, nghịch biến của hàm số.
Giải các bài toán thực tế liên quan đến hàm số bậc hai.

Giải chi tiết

Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:

Dạng tổng quát của hàm số bậc hai: y = ax² + bx + c (a ≠ 0).
Tọa độ đỉnh của parabol: I(-b/2a, -Δ/4a), với Δ = b² - 4ac.
Trục đối xứng của parabol: x = -b/2a.
Hàm số đồng biến trên khoảng (-∞, -b/2a) nếu a > 0 và trên khoảng (-b/2a, +∞) nếu a < 0.
Hàm số nghịch biến trên khoảng (-∞, -b/2a) nếu a < 0 và trên khoảng (-b/2a, +∞) nếu a > 0.

Ví dụ: Xét hàm số y = x² - 4x + 3.

a = 1, b = -4, c = 3.
Δ = (-4)² - 4 * 1 * 3 = 16 - 12 = 4.
Tọa độ đỉnh: I(2, -1).
Trục đối xứng: x = 2.
Hàm số nghịch biến trên khoảng (-∞, 2) và đồng biến trên khoảng (2, +∞).

Mẹo giải nhanh

Để giải nhanh bài tập này, học sinh có thể sử dụng các công thức và tính chất đã học. Ngoài ra, việc vẽ đồ thị hàm số cũng giúp học sinh dễ dàng hình dung và tìm ra lời giải.

Bài tập tương tự

Để rèn luyện kỹ năng giải toán, học sinh có thể làm thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác.

Lưu ý quan trọng

Khi giải bài tập về hàm số bậc hai, học sinh cần chú ý đến điều kiện xác định của hàm số và các trường hợp đặc biệt. Ngoài ra, việc kiểm tra lại kết quả cũng rất quan trọng để đảm bảo tính chính xác.

Bảng tóm tắt kiến thức:

Khái niệm	Công thức
Tọa độ đỉnh	I(-b/2a, -Δ/4a)
Trục đối xứng	x = -b/2a
Δ (delta)	b² - 4ac

Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh sẽ tự tin hơn khi giải Bài 5 trang 127 SGK Toán 11 Tập 1 - Chân trời sáng tạo. Chúc các em học tốt!