Lý thuyết Phép tính lũy thừa - Toán 11 Chân trời sáng tạo
Tổng quan nội dung
Lý thuyết Phép tính lũy thừa - Toán 11 Chân trời sáng tạo
Bài viết này cung cấp đầy đủ và chi tiết lý thuyết về phép tính lũy thừa trong chương trình Toán 11 Chân trời sáng tạo.
Chúng ta sẽ cùng nhau khám phá các khái niệm cơ bản, tính chất quan trọng và các công thức liên quan đến lũy thừa, giúp bạn nắm vững kiến thức nền tảng để giải quyết các bài toán một cách hiệu quả.
1. Lũy thừa với số mũ nguyên - Lũy thừa với số mũ nguyên dương:
1. Lũy thừa với số mũ nguyên
- Lũy thừa với số mũ nguyên dương:
\({a^n} = \underbrace {a.a.a...a}_{n\,thừa\,số}\left( {a \in \mathbb{R},n \in \mathbb{N}*} \right)\).
- Lũy thừa với số mũ nguyên âm, số mũ 0:
\({a^{ - n}} = \frac{1}{{{a^n}}};{a^0} = 1\left( {n \in \mathbb{N}*,a \in \mathbb{R},a \ne 0} \right)\).
2. Căn bậc n
Cho số thực b và số nguyên \(n \ge 2\).
- Số a là căn bậc n của số b nếu \({a^n} = b\).
- Sự tồn tại căn bậc n:
+ Nếu n lẻ thì có duy nhất một căn bậc n của b, kí hiệu \(\sqrt[n]{b}\).
+ Nếu n chẵn thì:
- b < 0: không tồn tại căn bậc n của b.
- b = 0: có một căn bậc n của b là 0.
- b > 0: có hai căn bậc n của b đối với nhau, kí hiệu giá trị dương là \(\sqrt[n]{b}\) và giá trị âm là \( - \sqrt[n]{b}\).
+ Các tính chất:
- \(\sqrt[n]{a}.\sqrt[n]{b} = \sqrt[n]{{ab}}\)
- \(\frac{{\sqrt[n]{a}}}{{\sqrt[n]{b}}} = \sqrt[n]{{\frac{a}{b}}}\)
- \({\left( {\sqrt[n]{a}} \right)^m} = \sqrt[n]{{{a^m}}}\)
- \(\sqrt[m]{{\sqrt[n]{a}}} = \sqrt[{mn}]{a}\)
3. Lũy thừa với số mũ hữu tỉ
Cho số thực dương a và số hữu tỉ \(r = \frac{m}{n}\), trong đó \(m,n \in \mathbb{Z},n > 0\). Ta có:
\({a^r} = {a^{\frac{m}{n}}} = \sqrt[n]{{{a^m}}}\)
4. Lũy thừa với số mũ vô tỉ
Giả sử a là một số dương, \(\alpha \) là một số vô tỉ và \(\left( {{r_n}} \right)\) là một dãy số hữu tỉ sao cho \(\lim {r_n} = \alpha \). Khi đó \({a^\alpha } = \mathop {\lim }\limits_{n \to + \infty } = {a^{{r_n}}}\).
5. Tính chất của phép tính lũy thừa
Cho a, b là những số thực dương; \(\alpha ;\beta \) là những số thực bất kì. Khi đó:
\(\begin{array}{l}{a^\alpha }.{a^\beta } = {a^{\alpha + \beta }};\\\frac{{{a^\alpha }}}{{{a^\beta }}} = {a^{\alpha - \beta }};\\{\left( {{a^\alpha }} \right)^\beta } = {a^{\alpha \beta }};\\{\left( {ab} \right)^\alpha } = {a^\alpha }.{b^\alpha };\\{\left( {\frac{a}{b}} \right)^\alpha } = \frac{{{a^\alpha }}}{{{b^\alpha }}}.\end{array}\)
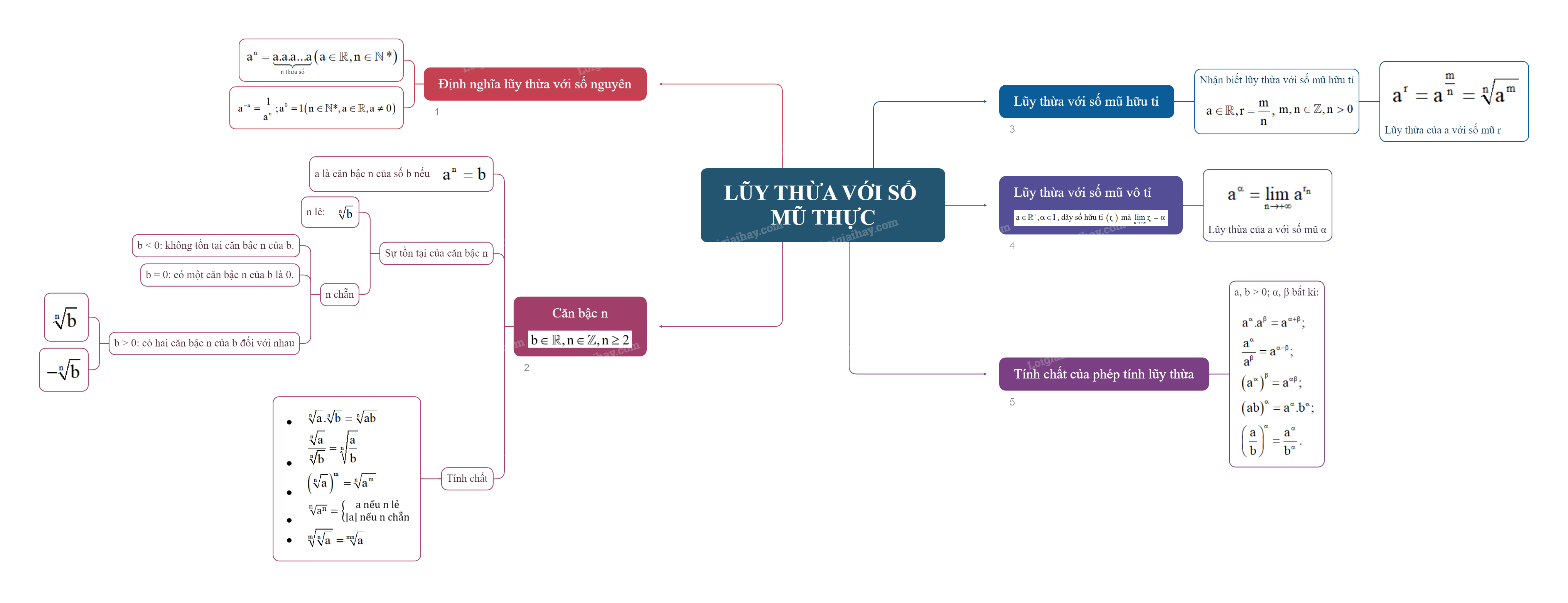
Lý Thuyết Phép Tính Lũy Thừa - Toán 11 Chân Trời Sáng Tạo: Tổng Quan Chi Tiết
Phép tính lũy thừa là một trong những khái niệm quan trọng trong toán học, đặc biệt là trong chương trình Toán 11 Chân trời sáng tạo. Việc nắm vững lý thuyết và các tính chất của phép tính lũy thừa là nền tảng để giải quyết các bài toán phức tạp hơn trong các chương trình học tiếp theo.
1. Khái Niệm Lũy Thừa
Lũy thừa của một số thực a (cơ số) với số nguyên dương n (số mũ) là tích của n thừa số bằng a, ký hiệu là an. Ví dụ: 23 = 2 * 2 * 2 = 8.
- Cơ số (a): Là số thực.
- Số mũ (n): Là số nguyên dương.
2. Các Tính Chất Của Phép Tính Lũy Thừa
Dưới đây là các tính chất quan trọng của phép tính lũy thừa mà bạn cần nắm vững:
- Lũy thừa của một tích: (a * b)n = an * bn
- Lũy thừa của một thương: (a / b)n = an / bn (với b ≠ 0)
- Lũy thừa của một lũy thừa: (am)n = am*n
- Lũy thừa bậc không: a0 = 1 (với a ≠ 0)
- Lũy thừa bậc một: a1 = a
3. Lũy Thừa Với Số Mũ Nguyên Âm
Nếu a ≠ 0 và n là số nguyên âm, thì an = 1 / a-n. Ví dụ: 2-3 = 1 / 23 = 1 / 8.
4. Lũy Thừa Với Số Mũ Hữu Tỉ
Nếu a > 0 và m/n là phân số tối giản, thì am/n = n√am. Ví dụ: 82/3 = 3√82 = 3√64 = 4.
5. Bài Tập Vận Dụng
Để củng cố kiến thức, hãy thử giải các bài tập sau:
- Tính giá trị của biểu thức: 34 + 2-2
- Rút gọn biểu thức: (x2)3 * x-1
- Tìm x biết: 2x = 16
6. Bảng Công Thức Lũy Thừa Quan Trọng
| Công thức | Mô tả |
|---|---|
| an * am = an+m | Nhân hai lũy thừa cùng cơ số |
| an / am = an-m | Chia hai lũy thừa cùng cơ số |
| (an)m = an*m | Lũy thừa của một lũy thừa |
7. Lưu Ý Khi Giải Bài Tập Về Lũy Thừa
- Luôn kiểm tra điều kiện của cơ số và số mũ.
- Sử dụng các tính chất của phép tính lũy thừa một cách linh hoạt để đơn giản hóa biểu thức.
- Chú ý đến dấu của cơ số và số mũ.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và quan trọng về lý thuyết phép tính lũy thừa trong chương trình Toán 11 Chân trời sáng tạo. Chúc bạn học tập tốt!