Lý thuyết Biến cố giao và quy tắc nhân xác suất - Toán 11 Chân trời sáng tạo
Tổng quan nội dung
Lý thuyết Biến cố giao và Quy tắc nhân xác suất - Toán 11 Chân trời sáng tạo
Bài học này cung cấp kiến thức nền tảng về biến cố giao và quy tắc nhân xác suất, một phần quan trọng trong chương trình Toán 11 Chân trời sáng tạo. Nắm vững lý thuyết này giúp học sinh giải quyết các bài toán xác suất một cách hiệu quả.
Chúng ta sẽ cùng tìm hiểu định nghĩa, tính chất của biến cố giao, cách tính xác suất của biến cố giao và ứng dụng của quy tắc nhân xác suất trong các bài toán thực tế.
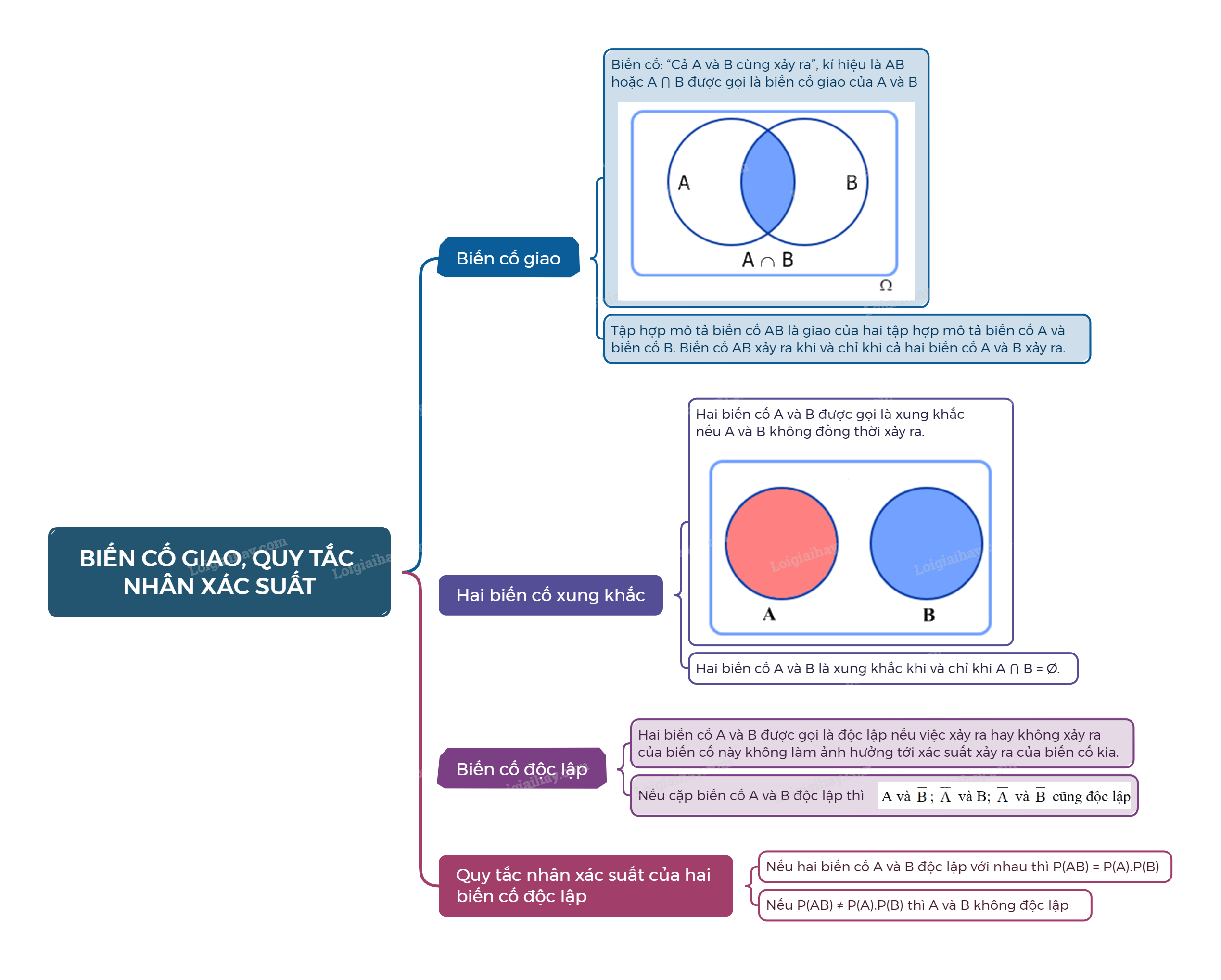
1. Biến cố giao Cho hai biến cố A và B.
1. Biến cố giao
Cho hai biến cố A và B. Biến cố: “Cả A và B cùng xảy ra”, kí hiệu AB hoặc \(A \cap B\) được gọi là biến cố giao của A và B.
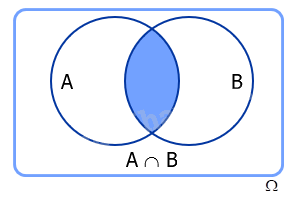
Chú ý: Tập hợp mô tả biến cố AB là giao của hai tập hợp mô tả biến cố A và biến cố B. Biến cố AB xảy ra khi và chỉ khi cả hai biến cố A và B xảy ra.
2. Hai biến cố xung khắc
Hai biến cố A và B được gọi là xung khắc nếu A và B không đồng thời xảy ra.
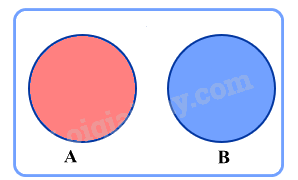
Chú ý: Hai biến cố A và B là xung khắc khi và chỉ khi \(A \cap B = \emptyset \).
3. Biến cố độc lập
Hai biến cố A và B được gọi là độc lập nếu việc xảy ra hay không xảy ra của biến cố này không làm ảnh hưởng tới xác suất xảy ra của biến cố kia.
Nhận xét: Nếu hai biến cố A và B độc lập thì A và \(\overline B \); \(\overline A \) và B; \(\overline A \) và \(\overline B \) cũng độc lập.
4. Quy tắc nhân xác suất của hai biến cố độc lập
Nếu hai biến cố A và B độc lập với nhau thì \(P\left( {AB} \right) = P\left( A \right).P\left( B \right)\).
Chú ý: Từ quy tắc nhân xác suất ta thấy, nếu \(P\left( {AB} \right) \ne P\left( A \right)P\left( B \right)\) thì hai biến cố A và B không độc lập.
Lý thuyết Biến cố giao và Quy tắc nhân xác suất - Toán 11 Chân trời sáng tạo: Giải thích chi tiết và bài tập minh họa
Trong chương trình Toán 11 Chân trời sáng tạo, phần xác suất đóng vai trò quan trọng trong việc phát triển tư duy logic và khả năng giải quyết vấn đề. Một trong những nội dung cốt lõi của phần này là Lý thuyết Biến cố giao và Quy tắc nhân xác suất. Bài viết này sẽ cung cấp một cái nhìn toàn diện về chủ đề này, bao gồm định nghĩa, tính chất, công thức và các ví dụ minh họa chi tiết.
1. Biến cố giao là gì?
Biến cố giao của hai biến cố A và B (ký hiệu A ∩ B) là biến cố mà cả A và B đều xảy ra. Nói cách khác, kết quả của phép thử phải đồng thời thỏa mãn cả điều kiện của A và điều kiện của B.
- Ví dụ: Tung một con xúc xắc.
- A: Xuất hiện mặt số chẵn.
- B: Xuất hiện mặt số lớn hơn 3.
- A ∩ B: Xuất hiện mặt số chẵn và lớn hơn 3 (tức là 4 hoặc 6).
2. Tính chất của biến cố giao
Một số tính chất quan trọng của biến cố giao:
- P(A ∩ B) ≤ min{P(A), P(B)}: Xác suất của biến cố giao không lớn hơn xác suất của mỗi biến cố thành phần.
- Nếu A và B là hai biến cố độc lập thì P(A ∩ B) = P(A) * P(B).
3. Quy tắc nhân xác suất
Quy tắc nhân xác suất cho phép tính xác suất của biến cố giao khi các biến cố không độc lập. Công thức tổng quát:
P(A ∩ B) = P(A) * P(B|A) = P(B) * P(A|B)
Trong đó:
- P(B|A) là xác suất của biến cố B khi biết biến cố A đã xảy ra (xác suất có điều kiện).
- P(A|B) là xác suất của biến cố A khi biết biến cố B đã xảy ra (xác suất có điều kiện).
4. Ví dụ minh họa ứng dụng Quy tắc nhân xác suất
Bài toán: Một hộp chứa 5 quả bóng đỏ và 3 quả bóng xanh. Lấy ngẫu nhiên 2 quả bóng từ hộp. Tính xác suất để cả hai quả bóng đều màu đỏ.
Giải:
Gọi A là biến cố “quả bóng thứ nhất lấy được màu đỏ”.
Gọi B là biến cố “quả bóng thứ hai lấy được màu đỏ”.
Ta cần tính P(A ∩ B) = P(A) * P(B|A)
P(A) = 5/8 (xác suất lấy được quả bóng đỏ ở lần lấy thứ nhất)
P(B|A) = 4/7 (xác suất lấy được quả bóng đỏ ở lần lấy thứ hai, khi đã lấy được một quả bóng đỏ ở lần lấy thứ nhất)
Vậy, P(A ∩ B) = (5/8) * (4/7) = 20/56 = 5/14
5. Bài tập luyện tập
Để củng cố kiến thức, bạn có thể thử giải các bài tập sau:
- Bài 1: Tung hai con xúc xắc. Tính xác suất để tổng số chấm trên hai con xúc xắc bằng 7.
- Bài 2: Rút một lá bài từ bộ bài 52 lá. Tính xác suất để lá bài đó là át hoặc là rô.
6. Kết luận
Lý thuyết Biến cố giao và Quy tắc nhân xác suất là nền tảng quan trọng để hiểu và giải quyết các bài toán xác suất phức tạp hơn. Việc nắm vững các định nghĩa, tính chất và công thức liên quan sẽ giúp bạn tự tin hơn trong quá trình học tập và làm bài tập. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải quyết vấn đề.
Chúc bạn học tốt!