Bài 5 trang 120 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Bài 5 trang 120 SGK Toán 11 Tập 1 - Chân trời sáng tạo
Bài 5 thuộc chương trình Toán 11 Tập 1, sách Chân trời sáng tạo, tập trung vào việc ôn tập về hàm số và đồ thị. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng áp dụng toán học vào cuộc sống.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
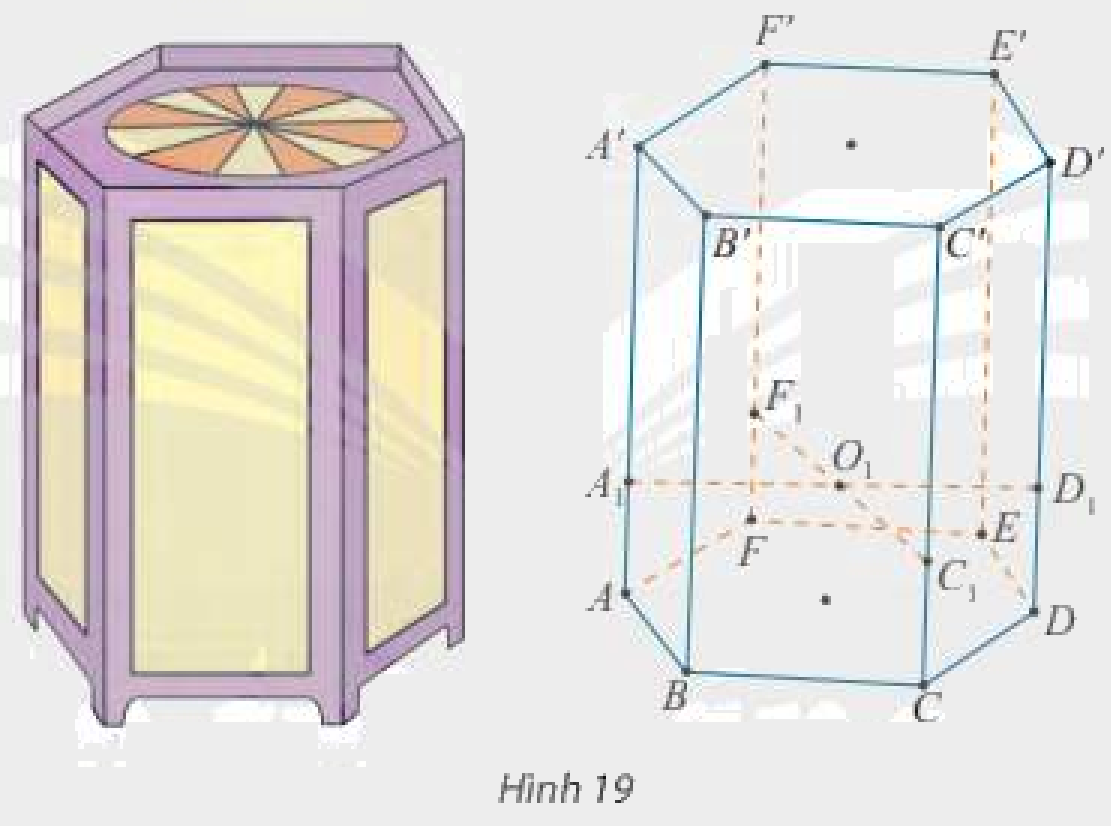
Để làm một khung lồng đèn kéo quân hình lăng trụ lục giác\(ABCDEF.A'B'C'D'E'F'\), Bình gắn hai thanh tre \({A_1}{D_1},{F_1}{C_1}\) song song với mặt phẳng đáy và cắt nhau tại \({O_1}\) (Hình 19).
Đề bài
Để làm một khung lồng đèn kéo quân hình lăng trụ lục giác\(ABCDEF.A'B'C'D'E'F'\), Bình gắn hai thanh tre \({A_1}{D_1},{F_1}{C_1}\) song song với mặt phẳng đáy và cắt nhau tại \({O_1}\) (Hình 19).
a) Xác định giao tuyến của \(mp\left( {{A_1}{D_1},{F_1}{C_1}} \right)\) với các mặt bên của lăng trụ.
b) Cho biết \(A'{A_1} = 6A{A_1}\) và \(AA' = 70{\rm{ }}cm\). Tính \(C{C_1}\) và \({C_1}C'\).
Phương pháp giải - Xem chi tiết
‒ Để tìm giao tuyến của hai mặt phẳng, ta có 2 cách:
+ Cách 1: Tìm 2 điểm chung phân biệt. Giao tuyến là đường thẳng đi qua hai điểm chung.
+ Cách 2: Tìm 1 điểm chung và 2 đường thẳng song song nằm trên mỗi mặt phẳng. Giao tuyến là đường thẳng đi qua điểm chung và song song với hai đường thẳng đó.
‒ Sử dụng định lí Thalès.
Lời giải chi tiết
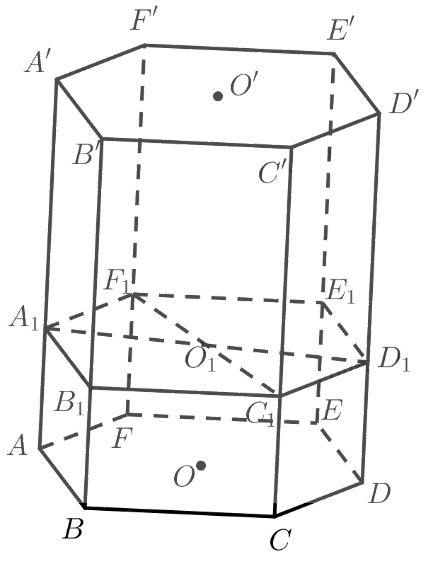
a) Gọi \({B_1},{E_1}\) lần lượt là giao điểm của \(mp\left( {{A_1}{D_1},{F_1}{C_1}} \right)\) với \(BB',EE'\).
Ta có:
\(\left. \begin{array}{l}{A_1}{D_1}\parallel \left( {ABC{\rm{DEF}}} \right)\\{F_1}{C_1}\parallel \left( {ABC{\rm{DEF}}} \right)\\{A_1}{D_1},{F_1}{C_1} \subset mp\left( {{A_1}{D_1},{F_1}{C_1}} \right)\end{array} \right\} \Rightarrow mp\left( {{A_1}{D_1},{F_1}{C_1}} \right)\parallel \left( {ABC{\rm{DEF}}} \right)\)
Vậy giao tuyến của \(mp\left( {{A_1}{D_1},{F_1}{C_1}} \right)\) với các mặt bên của lăng trụ là:
\(\begin{array}{l}mp\left( {{A_1}{D_1},{F_1}{C_1}} \right) \cap \left( {ABB'A'} \right) = {A_1}{B_1}\\mp\left( {{A_1}{D_1},{F_1}{C_1}} \right) \cap \left( {BCC'B'} \right) = {B_1}{C_1}\\mp\left( {{A_1}{D_1},{F_1}{C_1}} \right) \cap \left( {C{\rm{DD'C'}}} \right) = {C_1}{D_1}\\mp\left( {{A_1}{D_1},{F_1}{C_1}} \right) \cap \left( {DEE'D'} \right) = {D_1}{E_1}\\mp\left( {{A_1}{D_1},{F_1}{C_1}} \right) \cap \left( {EFF'E'} \right) = {E_1}{F_1}\\mp\left( {{A_1}{D_1},{F_1}{C_1}} \right) \cap \left( {AFF'A'} \right) = {A_1}{F_1}\end{array}\)
b) \(ABCDEF.A'B'C'D'E'F'\) là hình lăng trụ \( \Rightarrow CC' = AA' = 70\left( {cm} \right)\)
\(A'{A_1} = 6A{A_1} \Rightarrow A{A_1} = \frac{1}{7}AA' = 10\left( {cm} \right)\)
\(mp\left( {{A_1}{D_1},{F_1}{C_1}} \right)\parallel \left( {ABC{\rm{DEF}}} \right)\parallel \left( {A'B'C'{\rm{D'E'F'}}} \right)\)
\(\begin{array}{l} \Rightarrow \frac{{C{C_1}}}{{CC'}} = \frac{{A{A_1}}}{{AA'}} \Leftrightarrow C{C_1} = \frac{{CC'.A{A_1}}}{{AA'}} = \frac{{70.10}}{{70}} = 10\left( {cm} \right)\\ \Rightarrow {C_1}C' = CC' - C{C_1} = 70 - 10 = 60\left( {cm} \right)\end{array}\)
Bài 5 trang 120 SGK Toán 11 Tập 1 - Chân trời sáng tạo: Giải chi tiết và hướng dẫn
Bài 5 trang 120 SGK Toán 11 Tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về hàm số, đồ thị hàm số và các ứng dụng của chúng. Dưới đây là giải chi tiết bài tập này, cùng với hướng dẫn giải và các lưu ý quan trọng.
Nội dung bài tập
Bài 5 yêu cầu học sinh thực hiện các nhiệm vụ sau:
- Xác định tập xác định của hàm số.
- Tìm tập giá trị của hàm số.
- Xác định tính đơn điệu của hàm số.
- Vẽ đồ thị hàm số.
- Giải các bài toán liên quan đến hàm số.
Giải chi tiết
Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
- Định nghĩa hàm số và các loại hàm số.
- Tập xác định và tập giá trị của hàm số.
- Tính đơn điệu của hàm số.
- Đồ thị hàm số và cách vẽ đồ thị.
Ví dụ, để xác định tập xác định của hàm số y = f(x), ta cần tìm các giá trị của x sao cho f(x) có nghĩa. Tương tự, để tìm tập giá trị của hàm số, ta cần tìm các giá trị của y mà f(x) có thể nhận được.
Hướng dẫn giải
Dưới đây là một số hướng dẫn giải bài tập:
- Đọc kỹ đề bài và xác định yêu cầu của bài tập.
- Sử dụng các kiến thức đã học để giải quyết bài tập.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
Lưu ý quan trọng
Khi giải bài tập về hàm số, học sinh cần lưu ý những điều sau:
- Nắm vững định nghĩa và các tính chất của hàm số.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm vẽ đồ thị.
- Rèn luyện kỹ năng tư duy logic và khả năng áp dụng toán học vào cuộc sống.
Bài tập tương tự
Để củng cố kiến thức, học sinh có thể giải các bài tập tương tự sau:
- Bài 1 trang 120 SGK Toán 11 Tập 1 - Chân trời sáng tạo
- Bài 2 trang 120 SGK Toán 11 Tập 1 - Chân trời sáng tạo
- Bài 3 trang 120 SGK Toán 11 Tập 1 - Chân trời sáng tạo
Kết luận
Bài 5 trang 120 SGK Toán 11 Tập 1 - Chân trời sáng tạo là một bài tập quan trọng, giúp học sinh củng cố kiến thức về hàm số và đồ thị hàm số. Hy vọng với lời giải chi tiết và hướng dẫn giải trên, học sinh có thể tự tin giải bài tập này và đạt kết quả tốt trong học tập.
| Hàm số | Tập xác định | Tập giá trị |
|---|---|---|
| y = x2 | R | [0, +∞) |
| y = 1/x | x ≠ 0 | R \ {0} |
Nguồn: tusach.vn - Giải bài tập Toán 11 nhanh chóng và chính xác.