Đề bài
Cho hình vuông \(ABCD\) và tam giác đều \(SAB\) cạnh \(a\) nằm trong hai mặt phẳng vuông góc với nhau. Gọi \(M,N\) lần lượt là trung điểm của \(AB\) và \(AD\).
a) Chứng minh rằng \(\left( {SMD} \right) \bot \left( {SNC} \right)\).
b) Tính khoảng cách từ \(M\) đến mặt phẳng \(\left( {SNC} \right)\).
Phương pháp giải - Xem chi tiết
‒ Cách chứng minh hai mặt phẳng vuông góc: chứng minh mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng.
‒ Cách tính khoảng cách từ một điểm đến một mặt phẳng: Tính khoảng cách từ điểm đó đến hình chiếu của nó lên mặt phẳng.
Lời giải chi tiết
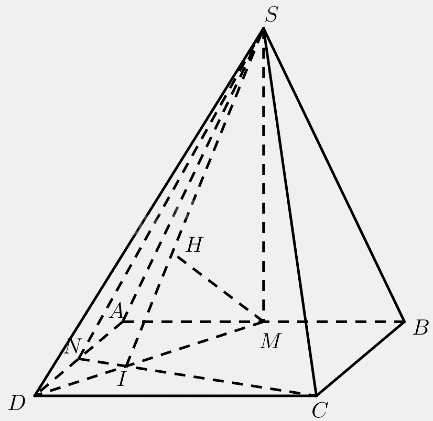
Gọi \(I = CN \cap DM\)
\(\Delta SAB\) đều \( \Rightarrow SM \bot AB\)
Mà \(\left( {SAB} \right) \bot \left( {ABCD} \right),\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\)
\( \Rightarrow SM \bot \left( {ABCD} \right) \Rightarrow SM \bot CN\)
\(\Delta A{\rm{D}}M = \Delta DCN\left( {c.g.c} \right) \Rightarrow \widehat {AM{\rm{D}}} = \widehat {CN{\rm{D}}}\)
Mà \(\widehat {AM{\rm{D}}} + \widehat {A{\rm{D}}M} = {90^ \circ }\)
\(\widehat {CN{\rm{D}}} + \widehat {A{\rm{D}}M} = {90^ \circ } \Rightarrow \widehat {NI{\rm{D}}} = {180^ \circ } - \left( {\widehat {CN{\rm{D}}} + \widehat {A{\rm{D}}M}} \right) = {90^ \circ } \Rightarrow CN \bot DM\)
\(\left. \begin{array}{l}\left. \begin{array}{l}SM \bot CN\\CN \bot DM\end{array} \right\} \Rightarrow CN \bot \left( {SM{\rm{D}}} \right)\\CN \subset \left( {SNC} \right)\end{array} \right\} \Rightarrow \left( {SNC} \right) \bot \left( {SM{\rm{D}}} \right)\)
b) Kẻ \(MH \bot SI\left( {H \in SI} \right)\)
\(CN \bot \left( {SM{\rm{D}}} \right) \Rightarrow CN \bot MH\)
\( \Rightarrow MH \bot \left( {SNC} \right) \Rightarrow d\left( {M,\left( {SNC} \right)} \right) = MH\)
\(\Delta C{\rm{D}}N\) vuông tại \(D\) có đường cao \(DI\)
\(DN = \frac{1}{2}A{\rm{D}} = \frac{a}{2},CN = \sqrt {C{{\rm{D}}^2} + D{N^2}} = \frac{{a\sqrt 5 }}{2},DI = \frac{{C{\rm{D}}.DN}}{{CN}} = \frac{{a\sqrt 5 }}{5}\)
\(DM = CN = \frac{{a\sqrt 5 }}{2} \Rightarrow MI = DM - DI = \frac{{3a\sqrt 5 }}{{10}}\)
\(\Delta SAB\) đều \( \Rightarrow SM = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}\)
\(\Delta SMI\) vuông tại \(M\) có đường cao \(MH\)
\( \Rightarrow MH = \frac{{SM.MI}}{{\sqrt {S{M^2} + M{I^2}} }} = \frac{{3a\sqrt 2 }}{8}\)
Vậy \(d\left( {M,\left( {SNC} \right)} \right) = \frac{{3a\sqrt 2 }}{8}\)
