Lý thuyết Hai đường thẳng vuông góc - Toán 11 Chân trời sáng tạo
Tổng quan nội dung
Lý thuyết Hai đường thẳng vuông góc - Toán 11 Chân trời sáng tạo
Bài học này cung cấp kiến thức nền tảng về mối quan hệ vuông góc giữa hai đường thẳng trong không gian. Chúng ta sẽ tìm hiểu điều kiện để hai đường thẳng vuông góc, cách xác định góc giữa hai đường thẳng và ứng dụng của lý thuyết này trong giải toán.
Nội dung bài học được trình bày một cách dễ hiểu, có ví dụ minh họa và bài tập thực hành để giúp học sinh nắm vững kiến thức.
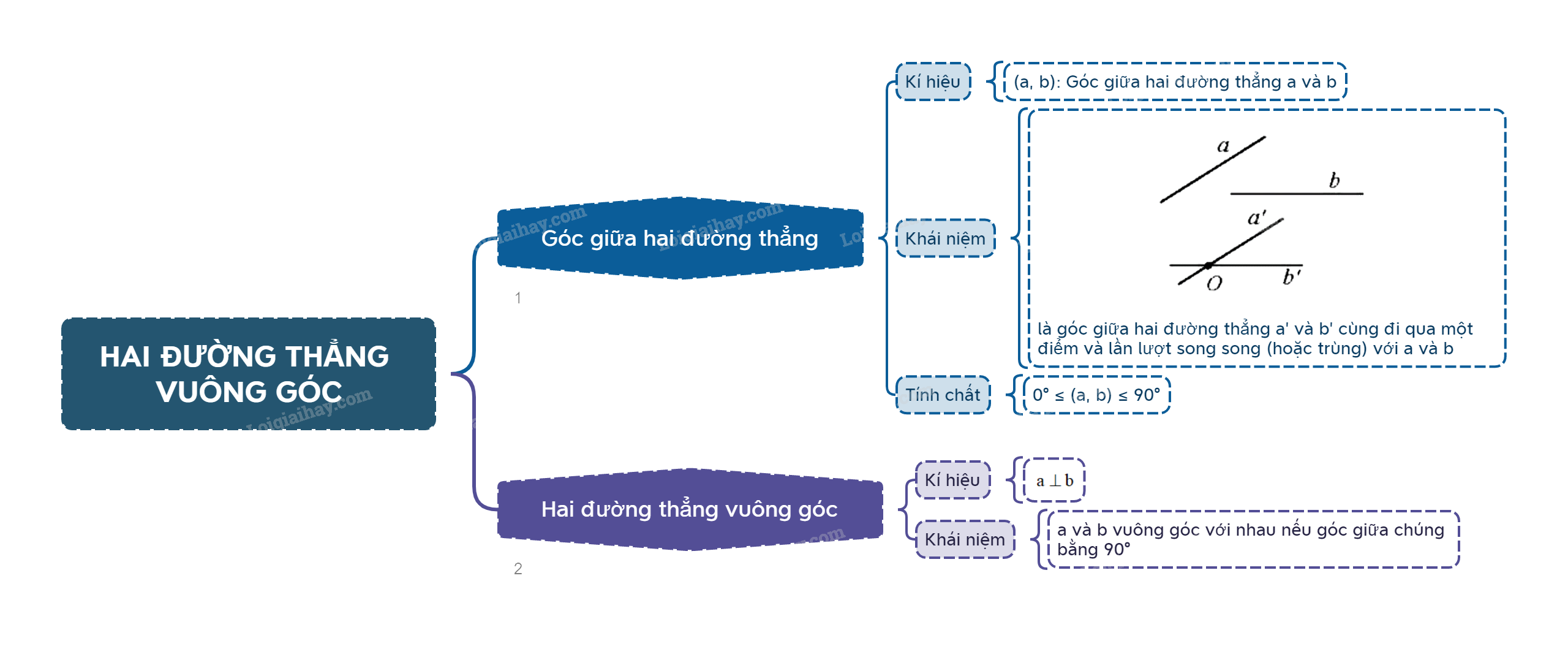
1. Góc giữa hai đường thẳng trong không gian Góc giữa hai đường thẳng a, b trong không gian, kí hiệu (a, b), là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm và lần lượt song song với a và b.
1. Góc giữa hai đường thẳng trong không gian
Góc giữa hai đường thẳng a, b trong không gian, kí hiệu (a, b), là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm và lần lượt song song với a và b.
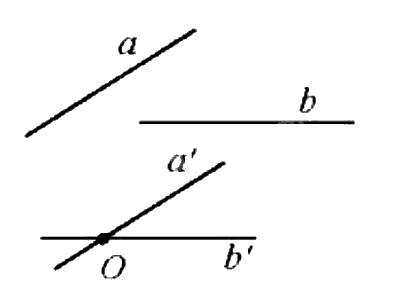
Chú ý: Góc giữa hai đường thẳng nhận giá trị từ \({0^0}\) đến \({90^0}\).
2. Hai đường thẳng vuông góc
Hai đường thẳng a, b được gọi là vuông góc với nhau, kí hiệu \(a \bot b\), nếu góc giữa chúng bằng \({90^0}\).
Lý Thuyết Hai Đường Thẳng Vuông Góc - Toán 11 Chân Trời Sáng Tạo: Giải Thích Chi Tiết và Bài Tập Vận Dụng
Trong chương trình Toán 11 Chân Trời Sáng Tạo, kiến thức về đường thẳng và mặt phẳng đóng vai trò quan trọng. Một trong những nội dung cốt lõi là lý thuyết về hai đường thẳng vuông góc. Bài viết này sẽ cung cấp một cái nhìn toàn diện về chủ đề này, bao gồm định nghĩa, điều kiện, tính chất và ứng dụng thực tế.
1. Định Nghĩa Hai Đường Thẳng Vuông Góc
Hai đường thẳng được gọi là vuông góc khi và chỉ khi góc giữa chúng bằng 90 độ. Điều này có nghĩa là, nếu d1 và d2 là hai đường thẳng vuông góc, thì góc (d1, d2) = 90o.
2. Điều Kiện Để Hai Đường Thẳng Vuông Góc
Để xác định hai đường thẳng có vuông góc hay không, chúng ta có thể sử dụng các điều kiện sau:
- Trong không gian: Hai đường thẳng d1 và d2 vuông góc khi và chỉ khi tích vô hướng của hai vector chỉ phương của chúng bằng 0. Nếu u là vector chỉ phương của d1 và v là vector chỉ phương của d2, thì d1 ⊥ d2 ⇔ u.v = 0.
- Trong mặt phẳng: Hai đường thẳng d1: a1x + b1y + c1 = 0 và d2: a2x + b2y + c2 = 0 vuông góc khi và chỉ khi a1a2 + b1b2 = 0.
3. Tính Chất của Hai Đường Thẳng Vuông Góc
Một số tính chất quan trọng của hai đường thẳng vuông góc:
- Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại.
- Trong không gian, nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
4. Ứng Dụng của Lý Thuyết Hai Đường Thẳng Vuông Góc
Lý thuyết này có nhiều ứng dụng trong giải toán hình học không gian, đặc biệt là trong việc:
- Xác định mối quan hệ giữa các đường thẳng và mặt phẳng.
- Tính góc giữa hai đường thẳng.
- Chứng minh các tính chất hình học.
5. Bài Tập Vận Dụng
Bài 1: Cho hai đường thẳng d1 và d2 có vector chỉ phương lần lượt là u = (1, -2, 3) và v = (2, 1, -1). Xác định xem hai đường thẳng này có vuông góc hay không?
Giải: Tính tích vô hướng của u và v: u.v = (1)(2) + (-2)(1) + (3)(-1) = 2 - 2 - 3 = -3. Vì u.v ≠ 0, nên hai đường thẳng d1 và d2 không vuông góc.
Bài 2: Tìm điều kiện của m để hai đường thẳng d1: y = mx + 1 và d2: y = -1/m x + 2 vuông góc với nhau.
Giải: Hai đường thẳng vuông góc khi tích của các hệ số góc bằng -1. Vậy m * (-1/m) = -1, điều này luôn đúng với mọi m ≠ 0.
6. Mở Rộng và Liên Hệ
Lý thuyết hai đường thẳng vuông góc là nền tảng cho nhiều kiến thức nâng cao hơn trong hình học không gian, như khoảng cách giữa hai đường thẳng chéo nhau, góc giữa hai mặt phẳng, và các bài toán về hình chiếu. Việc nắm vững lý thuyết này sẽ giúp bạn giải quyết các bài toán phức tạp một cách hiệu quả.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về Lý thuyết Hai đường thẳng vuông góc - Toán 11 Chân trời sáng tạo. Hãy luyện tập thêm nhiều bài tập để củng cố kiến thức và đạt kết quả tốt nhất!