Bài 1 trang 56 SGK Toán 11 tập 2 – Chân trời sáng tạo
Tổng quan nội dung
Bài 1 trang 56 SGK Toán 11 tập 2 – Chân trời sáng tạo
Bài 1 trang 56 SGK Toán 11 tập 2 thuộc chương trình Toán 11 Chân trời sáng tạo, tập trung vào việc ôn tập chương 3: Hàm số lượng giác. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số lượng giác, đồ thị hàm số lượng giác và các phép biến đổi lượng giác để giải quyết các bài toán cụ thể.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu và đáp án chính xác cho Bài 1 trang 56, giúp học sinh hiểu rõ bản chất bài toán và rèn luyện kỹ năng giải toán.
Cho hình chóp (S.ABCD) có đáy là hình thoi (ABCD) cạnh (a). Cho biết (SA = asqrt 3 ,SA bot AB) và (SA bot A{rm{D}}).
Đề bài
Cho hình chóp \(S.ABCD\) có đáy là hình thoi \(ABCD\) cạnh \(a\). Cho biết \(SA = a\sqrt 3 ,SA \bot AB\) và \(SA \bot A{\rm{D}}\). Tính góc giữa \(SB\) và \(C{\rm{D}}\), \(S{\rm{D}}\) và \(C{\rm{B}}\).
Phương pháp giải - Xem chi tiết
Cách xác định góc giữa hai đường thẳng \(a\) và \(b\):
Bước 1: Lấy một điểm \(O\) bất kì.
Bước 2: Qua điểm \(O\) dựng đường thẳng \(a'\parallel a\) và đường thẳng \(b'\parallel b\).
Bước 3: Tính \(\left( {a,b} \right) = \left( {a',b'} \right)\).
Lời giải chi tiết
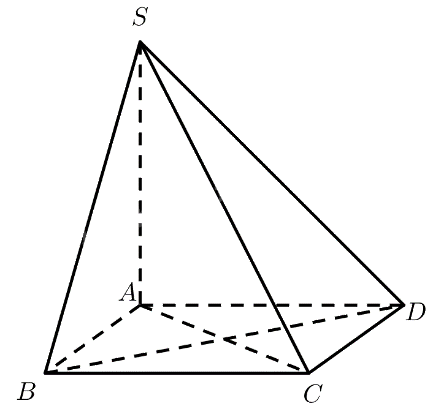
a) Ta có: \(C{\rm{D}}\parallel AB \Rightarrow \left( {SB,C{\rm{D}}} \right) = \left( {SB,AB} \right) = \widehat {SBA}\).
\(\tan \widehat {SBA} = \frac{{SA}}{{AB}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \Rightarrow \widehat {SBA} = {60^ \circ }\)
Vậy \(\left( {SB,C{\rm{D}}} \right) = {60^ \circ }\).
a) Ta có: \(C{\rm{B}}\parallel AD \Rightarrow \left( {SD,C{\rm{B}}} \right) = \left( {SD,AD} \right) = \widehat {S{\rm{D}}A}\).
\(\tan \widehat {SDA} = \frac{{SA}}{{AD}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \Rightarrow \widehat {SDA} = {60^ \circ }\)
Vậy \(\left( {SD,C{\rm{B}}} \right) = {60^ \circ }\).
Bài 1 trang 56 SGK Toán 11 tập 2 – Chân trời sáng tạo: Giải chi tiết và hướng dẫn
Bài 1 trang 56 SGK Toán 11 tập 2 Chân trời sáng tạo là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về hàm số lượng giác đã được học. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Nội dung bài tập
Bài 1 yêu cầu học sinh thực hiện các nhiệm vụ sau:
- Xác định tập xác định của hàm số lượng giác.
- Tìm tập giá trị của hàm số lượng giác.
- Xác định tính chẵn, lẻ của hàm số lượng giác.
- Vẽ đồ thị hàm số lượng giác.
- Giải các phương trình lượng giác cơ bản.
Lời giải chi tiết
Để giải bài 1 trang 56, học sinh cần nắm vững các kiến thức sau:
- Định nghĩa hàm số lượng giác (sin, cos, tan, cot).
- Tập xác định và tập giá trị của hàm số lượng giác.
- Tính chẵn, lẻ của hàm số lượng giác.
- Đồ thị hàm số lượng giác.
- Các phương pháp giải phương trình lượng giác cơ bản.
Ví dụ, xét hàm số y = sin(x).
- Tập xác định: R
- Tập giá trị: [-1, 1]
- Tính chẵn, lẻ: Hàm số lẻ (vì sin(-x) = -sin(x))
- Đồ thị: Đồ thị hàm số sin(x) là một đường cong lượn sóng, có chu kỳ 2π.
Hướng dẫn giải bài tập tương tự
Để giải các bài tập tương tự, học sinh có thể áp dụng các bước sau:
- Đọc kỹ đề bài và xác định yêu cầu của bài tập.
- Xác định hàm số lượng giác cần xét.
- Áp dụng các kiến thức đã học để giải bài tập.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
Mở rộng kiến thức
Ngoài việc giải bài tập, học sinh nên tìm hiểu thêm về các ứng dụng của hàm số lượng giác trong thực tế, chẳng hạn như trong vật lý, kỹ thuật, và khoa học máy tính.
Lưu ý quan trọng
Khi giải bài tập về hàm số lượng giác, học sinh cần chú ý đến đơn vị đo góc (độ hoặc radian) và sử dụng máy tính bỏ túi để tính toán các giá trị lượng giác một cách chính xác.
Bảng tổng hợp công thức lượng giác quan trọng
| Công thức | Mô tả |
|---|---|
| sin2(x) + cos2(x) = 1 | Công thức lượng giác cơ bản |
| tan(x) = sin(x) / cos(x) | Công thức tính tan(x) |
| cot(x) = cos(x) / sin(x) | Công thức tính cot(x) |
Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh sẽ hiểu rõ hơn về Bài 1 trang 56 SGK Toán 11 tập 2 Chân trời sáng tạo và có thể tự tin giải các bài tập tương tự. Đừng quên truy cập tusach.vn để xem thêm nhiều tài liệu học tập hữu ích khác!