Lý thuyết Hàm số lượng giác và đồ thị - SGK Toán 11 Chân trời sáng tạo
Tổng quan nội dung
Lý Thuyết Hàm Số Lượng Giác và Đồ Thị - Nền Tảng Toán 11
Hàm số lượng giác đóng vai trò quan trọng trong chương trình Toán 11, đặc biệt là trong chương trình Chân Trời Sáng Tạo.
Nắm vững lý thuyết và kỹ năng vẽ đồ thị hàm số lượng giác là bước đệm vững chắc cho các kiến thức nâng cao hơn trong quá trình học tập.
1. Hàm số lượng giác
1. Hàm số lượng giác
- Quy tắc đặt tương ứng mỗi số thực x với số thực sinx được gọi là hàm số sin, kí hiệu y = sinx. Tập xác định của hàm số sin là \(\mathbb{R}\).
- Quy tắc đặt tương ứng mỗi số thực x với số thực cosx được gọi là hàm số cos, kí hiệu y = cosx. Tập xác định của hàm số côsin là \(\mathbb{R}\).
- Hàm số cho bằng công thức \(y = \frac{{\sin \alpha }}{{\cos \alpha }}\)được gọi là hàm số tang, kí hiệu là y = tanx. Tập xác định của hàm số tang là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\).
- Hàm số cho bằng công thức \(y = \frac{{\cos \alpha }}{{\sin \alpha }}\) được gọi là hàm số côtang, kí hiệu là y = cotx. Tập xác định của hàm số côtang là \(\mathbb{R}\backslash \left\{ {k\pi |k \in \mathbb{Z}} \right\}\).
2. Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn
a, Hàm số chẵn, hàm số lẻ
Cho hàm số y = f(x) có tập xác định là D.
Hàm số f(x) được gọi là hàm số chẵn nếu \(\forall x \in D\) thì \( - x \in D\) và \(f( - x) = f(x)\). Đồ thị của một hàm số chẵn nhận trục tung (Oy) làm trục đối xứng.
Hàm số f(x) được gọi là hàm số lẻ nếu \(\forall x \in D\) thì \( - x \in D\) và \(f( - x) = - f(x)\). Đồ thị của một hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.
b, Hàm số tuần hoàn
Hàm số y = f(x) có tập xác định D được gọi là hàm số tuần hoàn nếu tồn tại số T \( \ne \) 0 sao cho với mọi \(x \in D\) ta có \(x \pm T \in D\) và \(f(x + T) = f(x)\)
Số T dương nhỏ nhất thỏa mãn cách điều kiện trên (nêu có) được gọi là chu kì của hàm số tuần hoàn đó.
* Nhận xét:
Các hàm số y = sinx, y=cosx tuần hoàn chu kì 2\(\pi \).
Các hàm số y = tanx, y=cotx tuần hoàn chu kì \(\pi \).
3. Đồ thị của các hàm số lượng giác
a, Hàm số y = sinx
- Tập xác định là \(\mathbb{R}\).
- Tập giá trị là [-1;1].
- Là hàm số lẻ và tuần hoàn chu kì 2\(\pi \).
- Đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)\).
- Có đồ thị đối xứng qua gốc tọa độ và gọi là một đường hình sin.
b, Hàm số y = cosx
- Tập xác định là \(\mathbb{R}\).
- Tập giá trị là [-1;1].
- Là hàm số chẵn và tuần hoàn chu kì 2\(\pi \).
- Đồng biến trên mỗi khoảng \(\left( { - \pi + k2\pi ;k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {k2\pi ;\pi + k2\pi } \right)\).
- Có đồ thị là một đường hình sin đối xứng qua trục tung.
c, Hàm số y = tanx
- Tập xác định là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\).
- Tập giá trị là \(\mathbb{R}\).
- Là hàm số lẻ và tuần hoàn chu kì \(\pi \).
- Đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k\pi ;\frac{\pi }{2} + k\pi } \right)\), \(k \in \mathbb{Z}\).
- Có đồ thị đối xứng qua gốc tọa độ.
d, Hàm số y = cotx
- Tập xác định là \(\mathbb{R}\backslash \left\{ {k\pi |k \in \mathbb{Z}} \right\}\).
- Tập giá trị là \(\mathbb{R}\).
- Là hàm số lẻ và tuần hoàn chu kì \(\pi \).
- Đồng biến trên mỗi khoảng \(\left( {k\pi ;\pi + k\pi } \right)\), \(k \in \mathbb{Z}\).
- Có đồ thị đối xứng qua gốc tọa độ.
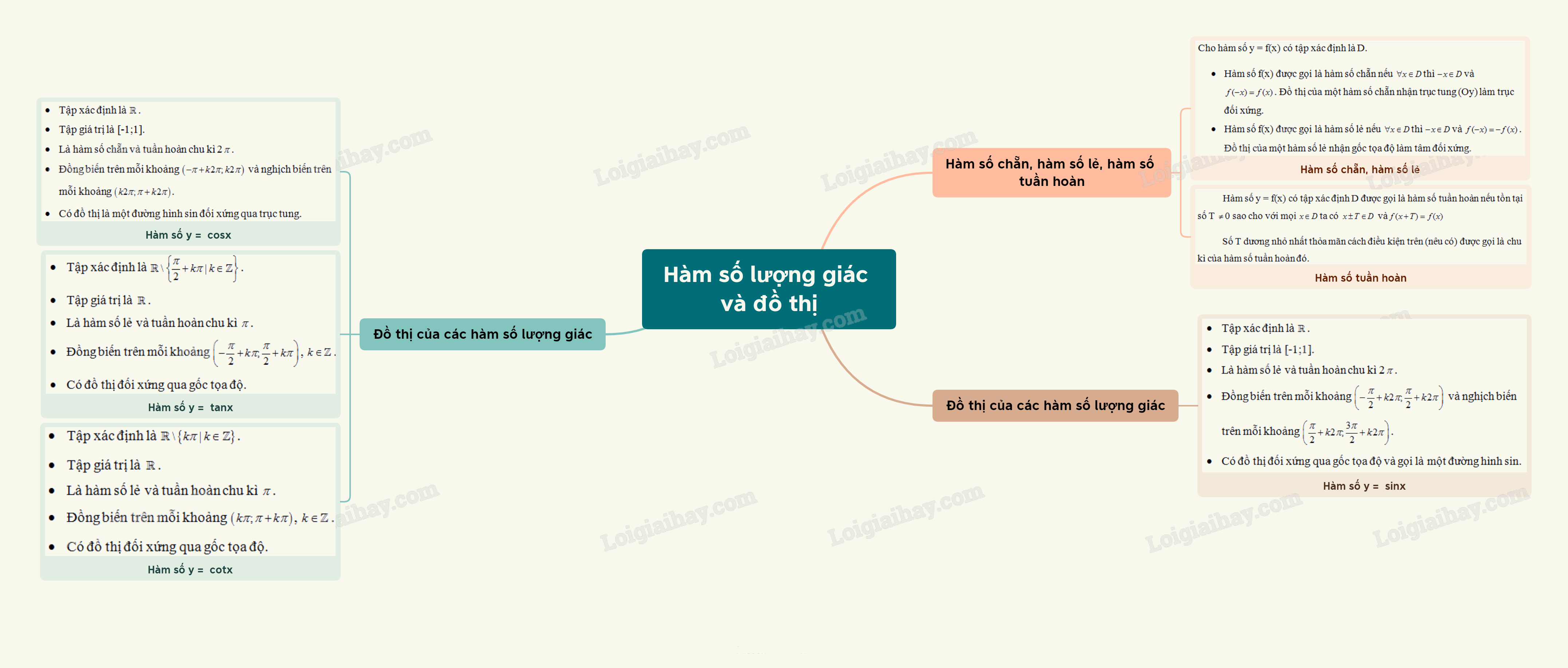
Lý Thuyết Hàm Số Lượng Giác và Đồ Thị - Toán 11 Chân Trời Sáng Tạo: Tổng Quan
Chương trình Toán 11 Chân Trời Sáng Tạo đi sâu vào nghiên cứu về hàm số lượng giác, một trong những chủ đề cốt lõi của giải tích. Việc hiểu rõ lý thuyết và nắm vững các kỹ năng liên quan đến đồ thị hàm số lượng giác là vô cùng quan trọng, không chỉ cho việc giải quyết các bài toán trong sách giáo khoa mà còn là nền tảng cho các kiến thức toán học nâng cao hơn.
1. Các Hàm Số Lượng Giác Cơ Bản
Trong chương này, chúng ta sẽ tìm hiểu về các hàm số lượng giác cơ bản sau:
- Hàm số sin (y = sin x): Định nghĩa, tập xác định, tập giá trị, tính tuần hoàn, tính chẵn lẻ.
- Hàm số cosin (y = cos x): Định nghĩa, tập xác định, tập giá trị, tính tuần hoàn, tính chẵn lẻ.
- Hàm số tang (y = tan x): Định nghĩa, tập xác định, tập giá trị, tính tuần hoàn.
- Hàm số cotang (y = cot x): Định nghĩa, tập xác định, tập giá trị, tính tuần hoàn.
2. Đồ Thị Hàm Số Lượng Giác
Việc vẽ và phân tích đồ thị hàm số lượng giác giúp chúng ta hiểu rõ hơn về tính chất của hàm số, cũng như ứng dụng của chúng trong thực tế. Dưới đây là một số điểm quan trọng khi vẽ đồ thị:
- Xác định tập xác định và tập giá trị của hàm số.
- Tìm các điểm đặc biệt trên đồ thị (điểm cực đại, điểm cực tiểu, điểm cắt trục).
- Sử dụng tính tuần hoàn của hàm số để vẽ đồ thị trên một khoảng lớn hơn.
3. Các Biến Đổi Hàm Số Lượng Giác
Để vẽ đồ thị của các hàm số lượng giác phức tạp hơn, chúng ta cần nắm vững các phép biến đổi sau:
- Biến đổi ngang (translation): y = f(x - a)
- Biến đổi dọc (vertical stretch/compression): y = A*f(x)
- Biến đổi pha (phase shift): y = f(x + b)
- Biến đổi biên độ (amplitude): y = A*f(x)
4. Phương Trình Lượng Giác Cơ Bản
Giải phương trình lượng giác là một kỹ năng quan trọng trong toán học. Một số phương trình lượng giác cơ bản thường gặp:
- sin x = a
- cos x = a
- tan x = a
- cot x = a
5. Ứng Dụng của Hàm Số Lượng Giác
Hàm số lượng giác có rất nhiều ứng dụng trong thực tế, bao gồm:
- Vật lý: Mô tả các hiện tượng dao động, sóng.
- Kỹ thuật: Thiết kế các mạch điện, xử lý tín hiệu.
- Địa lý: Tính toán khoảng cách, góc độ.
Bài Tập Vận Dụng
Để củng cố kiến thức, hãy thực hành giải các bài tập sau (tham khảo sách giáo khoa Toán 11 Chân Trời Sáng Tạo):
- Vẽ đồ thị hàm số y = 2sin(x - π/4).
- Giải phương trình cos(2x) = 1/2.
- Tìm tập xác định của hàm số y = tan(x + π/3).
Kết Luận
Lý thuyết hàm số lượng giác và đồ thị là một phần quan trọng của chương trình Toán 11 Chân Trời Sáng Tạo. Việc nắm vững kiến thức này sẽ giúp bạn tự tin hơn trong việc giải quyết các bài toán và ứng dụng toán học vào thực tế. Hãy dành thời gian ôn tập và thực hành thường xuyên để đạt kết quả tốt nhất!