Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải mục 2 trang 35, 36 SGK Toán 11 tập 1 - Chân trời sáng tạo
SGK Toán 11 - Chân trời sáng tạo
Toán 11 tập 1 - Chân trời sáng tạo
Chương 1 Hàm số lượng giác và phương trình lượng giác
Bài 5. Phương trình lượng giác cơ bản

Giải mục 2 trang 35, 36 SGK Toán 11 tập 1 - Chân trời sáng tạo

Giải mục 2 trang 35, 36 SGK Toán 11 tập 1 - Chân trời sáng tạo

Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Toán 11 tập 1 Chân trời sáng tạo. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, vì vậy chúng tôi luôn cố gắng mang đến những giải pháp tốt nhất để giúp bạn học tập hiệu quả.

Bài viết này sẽ tập trung vào việc giải mục 2 trang 35 và 36, giúp bạn hiểu rõ các khái niệm và phương pháp giải bài tập liên quan.

a) Có giá trị nào của x để (sinx = 1,5)không?

Hoạt động 2Thực hành 2

Hoạt động 2

    a) Có giá trị nào của x để \(sinx = 1,5\)không?

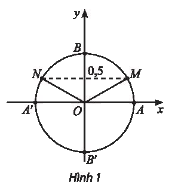
    b) Trong Hình 1, những điểm nào trên đường tròn lượng giác biểu diễn góc lượng giác x có \(sinx = 0,5\)? Xác định số đo của các góc lượng giác đó.

    Giải mục 2 trang 35, 36 SGK Toán 11 tập 1 - Chân trời sáng tạo 1

    Phương pháp giải:

    Quan sát hình và dựa vào tính chất \( - 1 \le sinx \le 1\).

    Lời giải chi tiết:

    a) Với mọi \(x \in \mathbb{R}\), ta có: \( - 1 \le sinx \le 1\)

    Do đó không có giá trị nào của x để \(sinx = 1,5\).

    b) Những điểm biểu diễn góc lượng giác có \(sinx = 0,5\) là M và N.

    Điểm M biểu diễn cho các góc lượng giác có số đo là \(\frac{\pi }{6} + k2\pi ,k \in \mathbb{Z}.\) 

    Điểm N biểu diễn cho các góc lượng giác có số đo là \(\frac{{5\pi }}{6} + k2\pi ,k \in \mathbb{Z}.\) 

    Thực hành 2

      Giải các phương trình sau:

      \(\begin{array}{l}a)\;sinx = \frac{{\sqrt 3 }}{2}\\b)\;sin(x + {30^o}) = sin(x + {60^o})\end{array}\)

      Phương pháp giải:

      Nếu \(\left| m \right| \le 1\) thì phương trình:

      • \({\mathop{\rm s}\nolimits} {\rm{inx}} = m \Leftrightarrow \sin x = \sin \alpha \)\( \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
      • \(\sin x = \sin {\alpha ^o} \Leftrightarrow \left[ \begin{array}{l}x = {\alpha ^o} + k{360^o}\\x = {180^o} - {\alpha ^o} + k{360^o}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\)

      Lời giải chi tiết:

      \(a)\;sinx = \frac{{\sqrt 3 }}{2}\)

      Vì \(sin\frac{\pi }{3} = \frac{{\sqrt 3 }}{2}\) nên \(sinx = \frac{{\sqrt 3 }}{2} \Leftrightarrow sin\frac{\pi }{3} = sin\frac{\pi }{3}\) \( \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}\\x = \pi - \frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}\end{array} \right.\)

      \( \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}\\x = \frac{{2\pi }}{3} + k2\pi ,k \in \mathbb{Z}\end{array} \right.\)

      Vậy phương trình có nghiệm là \(x = \frac{\pi }{3} + k2\pi \) hoặc \(x = \frac{{2\pi }}{3} + k2\pi \)\(,k \in \mathbb{Z}\).

      \(\begin{array}{l}b)\;sin(x + {30^o}) = sin(x + {60^o})\\ \Leftrightarrow \left[ \begin{array}{l}x + {30^o} = x + {60^o} + k{360^o},k \in \mathbb{Z}\\x + {30^o} = {180^o} - x - {60^o} + k{360^o},k \in \mathbb{Z}\end{array} \right.\\ \Leftrightarrow x = {45^o} + k{180^o},k \in \mathbb{Z}.\end{array}\)

      Vậy phương trình có nghiệm là \(x = {45^o} + k{180^o},k \in \mathbb{Z}\).

      Giải mục 2 trang 35, 36 SGK Toán 11 tập 1 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu

      Mục 2 của chương trình Toán 11 tập 1 Chân trời sáng tạo thường xoay quanh các chủ đề về hàm số bậc hai, bao gồm định nghĩa, tính chất, đồ thị và ứng dụng. Việc nắm vững kiến thức này là nền tảng quan trọng cho các chương trình học tiếp theo. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập trong mục 2 trang 35 và 36, kèm theo các giải thích rõ ràng và dễ hiểu.

      Nội dung chính của Mục 2 trang 35, 36

      • Bài 1: Thường yêu cầu xác định hàm số bậc hai dựa trên các thông tin cho trước (ví dụ: hệ số, đỉnh, điểm thuộc đồ thị).
      • Bài 2: Tập trung vào việc tìm tập xác định, tập giá trị, khoảng đồng biến, nghịch biến của hàm số bậc hai.
      • Bài 3: Yêu cầu vẽ đồ thị hàm số bậc hai, xác định tọa độ đỉnh, trục đối xứng và các điểm đặc biệt.
      • Bài 4: Liên quan đến việc giải các bài toán thực tế ứng dụng hàm số bậc hai (ví dụ: tính quỹ đạo của vật ném, tối ưu hóa diện tích).

      Giải chi tiết Bài 1: Xác định hàm số bậc hai

      Để xác định hàm số bậc hai, chúng ta cần biết các thông tin cơ bản như hệ số a, b, c hoặc tọa độ đỉnh, một điểm thuộc đồ thị. Ví dụ, nếu đề bài cho đỉnh I(x0, y0) và một điểm A(x1, y1) thuộc đồ thị, ta có thể sử dụng công thức:

      y = a(x - x0)2 + y0

      Sau đó, thay tọa độ điểm A vào phương trình để tìm giá trị của a.

      Giải chi tiết Bài 2: Tìm tập xác định, tập giá trị, khoảng đồng biến, nghịch biến

      Tập xác định của hàm số bậc hai là tập R (tất cả các số thực). Tập giá trị phụ thuộc vào dấu của hệ số a:

      • Nếu a > 0: Tập giá trị là [y0, +∞)
      • Nếu a < 0: Tập giá trị là (-∞, y0]

      Khoảng đồng biến và nghịch biến được xác định dựa trên trục đối xứng x = x0:

      • Nếu a > 0: Hàm số nghịch biến trên (-∞, x0) và đồng biến trên (x0, +∞)
      • Nếu a < 0: Hàm số đồng biến trên (-∞, x0) và nghịch biến trên (x0, +∞)

      Giải chi tiết Bài 3: Vẽ đồ thị hàm số bậc hai

      Để vẽ đồ thị hàm số bậc hai, ta thực hiện các bước sau:

      1. Xác định tọa độ đỉnh I(x0, y0) với x0 = -b/(2a) và y0 = -Δ/(4a) (Δ = b2 - 4ac).
      2. Xác định trục đối xứng x = x0.
      3. Xác định các điểm đặc biệt như giao điểm với trục Oy (x = 0) và giao điểm với trục Ox (y = 0).
      4. Vẽ parabol đi qua các điểm đã xác định.

      Giải chi tiết Bài 4: Ứng dụng hàm số bậc hai vào bài toán thực tế

      Các bài toán ứng dụng hàm số bậc hai thường yêu cầu chúng ta xây dựng mô hình toán học dựa trên các thông tin cho trước. Ví dụ, trong bài toán về quỹ đạo của vật ném, hàm số bậc hai mô tả mối quan hệ giữa chiều cao của vật và thời gian. Việc giải bài toán này đòi hỏi chúng ta phải hiểu rõ ý nghĩa của các hệ số trong hàm số và sử dụng các công thức vật lý liên quan.

      Lưu ý:

      • Luôn kiểm tra lại kết quả sau khi giải bài tập.
      • Sử dụng máy tính bỏ túi để tính toán nhanh chóng và chính xác.
      • Tham khảo thêm các tài liệu học tập khác để hiểu sâu hơn về kiến thức.

      Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải quyết các bài tập trong mục 2 trang 35, 36 SGK Toán 11 tập 1 Chân trời sáng tạo. Chúc bạn học tập tốt!

      Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

      CHỦ ĐỀ SÁCH XEM NHIỀU

      Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

      VỀ TUSACH.VN