Giải mục 4 trang 10, 11 SGK Toán 11 tập 2 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 4 trang 10, 11 SGK Toán 11 tập 2 - Chân trời sáng tạo
Chào mừng bạn đến với tusach.vn! Chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong sách giáo khoa Toán 11 tập 2, chương trình Chân trời sáng tạo. Bài viết này sẽ tập trung vào việc giải mục 4 trang 10 và 11, giúp bạn hiểu rõ hơn về các khái niệm và phương pháp giải toán.
Ta biết rằng, (sqrt 2 ) là một số vô tỉ có thể biểu diễn dưới dạng số thập phân vô hạn không tuần hoàn:
Hoạt động 4
Ta biết rằng, \(\sqrt 2 \) là một số vô tỉ có thể biểu diễn dưới dạng số thập phân vô hạn không tuần hoàn: \(\sqrt 2 = 1,414213562...\)
Cũng có thể coi \(\sqrt 2 \) là giới hạn của dãy số hữu tỉ \(\left( {{r_n}} \right)\):
\(1,4;1,41;1,414;1,4142;...\)
Từ đây, ta lập dãy số các luỹ thừa \(\left( {{3^{{r_n}}}} \right)\).
a) Bảng dưới cho biết những số hạng đầu tiên của dãy số \(\left( {{3^{{r_n}}}} \right)\) (làm tròn đến chữ số thập phân thứ chín). Sử dụng máy tính cầm tay, hãy tính số hạng thứ 6 và thứ 7 của dãy số này.

b) Nêu nhận xét về dãy số \(\left( {{3^{{r_n}}}} \right)\).
Phương pháp giải:
Sử dụng máy tính cầm tay để tính.
Lời giải chi tiết:
a) \({r_6} = {3^{1,414213}} = 4,728801466;{r_7} = {3^{1,4142134}} = 4,728803544\).
b) Ta thấy khi \(n \to + \infty \) thì \({3^{{r_n}}} \to {3^{\sqrt 2 }}\).
Thực hành 5
Sử dụng máy tính cầm tay, tính các luỹ thừa sau đây (làm tròn đến chữ số thập phân thứ sáu):
a) \(1,{2^{1,5}}\);
b) \({10^{\sqrt 3 }}\);
c) \({\left( {0,5} \right)^{ - \frac{2}{3}}}\).
Phương pháp giải:
Sử dụng máy tính cầm tay.
Lời giải chi tiết:
Để làm tròn đến chữ số thập phân thứ 6:

a,

b,
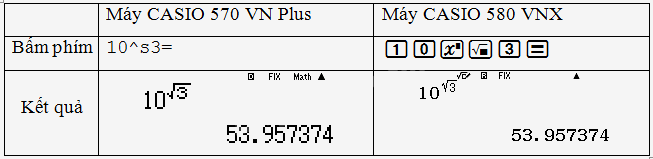
c,

Giải mục 4 trang 10, 11 SGK Toán 11 tập 2 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 4 trong SGK Toán 11 tập 2 chương trình Chân trời sáng tạo thường xoay quanh các chủ đề về đạo hàm của hàm số lượng giác và ứng dụng của đạo hàm trong việc khảo sát hàm số. Việc nắm vững kiến thức trong mục này là vô cùng quan trọng, không chỉ để giải quyết các bài tập trong sách giáo khoa mà còn là nền tảng cho các kiến thức nâng cao hơn trong chương trình học.
Nội dung chính của Mục 4
- Đạo hàm của các hàm số lượng giác cơ bản: sin(x), cos(x), tan(x), cot(x).
- Các công thức đạo hàm lượng giác: Cách tính đạo hàm của tổng, hiệu, tích, thương của các hàm số lượng giác.
- Ứng dụng đạo hàm để khảo sát hàm số lượng giác: Tìm cực trị, khoảng đồng biến, nghịch biến, điểm uốn của hàm số lượng giác.
Giải chi tiết bài tập trang 10, 11 SGK Toán 11 tập 2 - Chân trời sáng tạo
Dưới đây là giải chi tiết các bài tập trong mục 4 trang 10 và 11. Chúng tôi sẽ trình bày từng bước giải một cách rõ ràng, dễ hiểu, kèm theo các lưu ý quan trọng để bạn có thể tự tin áp dụng vào các bài tập tương tự.
Bài 1: Tính đạo hàm của các hàm số sau:
- y = 2sin(x) + 3cos(x)
- y = tan(x) - cot(x)
- y = sin2(x)
Giải:
- y' = 2cos(x) - 3sin(x)
- y' = 1/cos2(x) + 1/sin2(x)
- y' = 2sin(x)cos(x) = sin(2x)
Bài 2: Tìm đạo hàm của hàm số y = sin(x2 + 1)
Giải:
Sử dụng quy tắc chuỗi, ta có:
y' = cos(x2 + 1) * (2x) = 2xcos(x2 + 1)
Bài 3: Khảo sát hàm số y = x + cos(x)
Giải:
Bước 1: Tính đạo hàm y' = 1 - sin(x)
Bước 2: Tìm điểm dừng: y' = 0 => sin(x) = 1 => x = π/2 + kπ (k ∈ Z)
Bước 3: Lập bảng biến thiên và kết luận về khoảng đồng biến, nghịch biến, cực trị của hàm số.
Mẹo giải bài tập đạo hàm lượng giác
- Nắm vững các công thức đạo hàm lượng giác cơ bản.
- Sử dụng quy tắc chuỗi một cách linh hoạt.
- Kết hợp các kiến thức về đạo hàm và khảo sát hàm số để giải quyết các bài tập phức tạp.
- Thực hành thường xuyên để làm quen với các dạng bài tập khác nhau.
Tại sao nên chọn tusach.vn để học Toán 11?
tusach.vn là địa chỉ tin cậy cho các bạn học sinh muốn tìm kiếm lời giải bài tập Toán 11 nhanh chóng, chính xác và dễ hiểu. Chúng tôi cung cấp:
- Lời giải chi tiết, được trình bày rõ ràng, dễ theo dõi.
- Đội ngũ giáo viên giàu kinh nghiệm, luôn sẵn sàng hỗ trợ bạn.
- Cập nhật liên tục các bài giải mới nhất.
- Giao diện thân thiện, dễ sử dụng.
Hãy truy cập tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích khác!