Lý thuyết Hàm số mũ. Hàm số lôgarit - Toán 11 Chân trời sáng tạo
Tổng quan nội dung
Lý thuyết Hàm số mũ và Hàm số lôgarit - Toán 11 Chân Trời Sáng Tạo
Chào mừng bạn đến với chuyên mục lý thuyết Hàm số mũ và Hàm số lôgarit của chương trình Toán 11 Chân Trời Sáng Tạo tại tusach.vn.
Đây là một trong những chủ đề quan trọng, nền tảng cho các kiến thức toán học nâng cao hơn.
Chúng tôi cung cấp tài liệu học tập đầy đủ, chi tiết, giúp bạn dễ dàng nắm bắt và áp dụng kiến thức vào giải bài tập.
1. Hàm số mũ - Hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) được gọi là hàm số mũ cơ số a.
1. Hàm số mũ
- Hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) được gọi là hàm số mũ cơ số a.
- Hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) có:
+ Tập xác định: \(D = \mathbb{R}\).
+ Tập giá trị: \(T = \left( {0; + \infty } \right)\).
+ Hàm số liên tục trên \(\mathbb{R}\).
+ Sự biến thiên:
- Nếu a > 1 thì hàm số đồng biến trên \(\mathbb{R}\) và \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\mathop {\lim }\limits_{x \to - \infty } y = 0\).
- Nếu 0 < a < 1 thì hàm số nghịch biến trên \(\mathbb{R}\) và \(\mathop {\lim }\limits_{x \to + \infty } y = 0;\mathop {\lim }\limits_{x \to - \infty } y = + \infty \).
+ Đồ thị:
- Cắt trục tung tại điểm (0; 1), đi qua điểm (1; a).
- Nằm phía trên trục hoành.
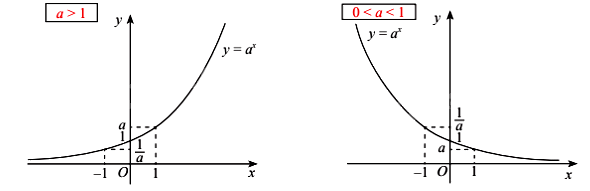
2. Hàm số lôgarit
- Hàm số \(y = {\log _a}x\left( {a > 0;a \ne 1} \right)\) được gọi là hàm số lôgarit cơ số a.
- Hàm số \(y = {\log _a}x\left( {a > 0;a \ne 1} \right)\) có:
+ Tập xác định: \(D = \left( {0; + \infty } \right)\).
+ Tập giá trị: \(T = \mathbb{R}\).
+ Hàm số liên tục trên \(\left( {0; + \infty } \right)\).
+ Sự biến thiên:
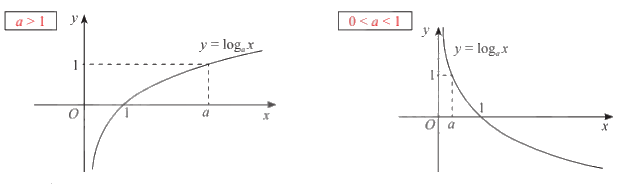
- Nếu a > 1 thì hàm số đồng biến trên \(\left( {0; + \infty } \right)\) và \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\mathop {\lim }\limits_{x \to {0^ + }} y = 0\).
- Nếu 0 < a < 1 thì hàm số nghịch biến trên \(\left( {0; + \infty } \right)\) và \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty ;\mathop {\lim }\limits_{x \to {0^ + }} y = + \infty \).
+ Đồ thị:
- Cắt trục hoành tại điểm (1; 0), đi qua điểm (a; 1).
- Nằm phía phải trục tung.
Lý Thuyết Hàm Số Mũ và Hàm Số Lôgarit - Toán 11 Chân Trời Sáng Tạo
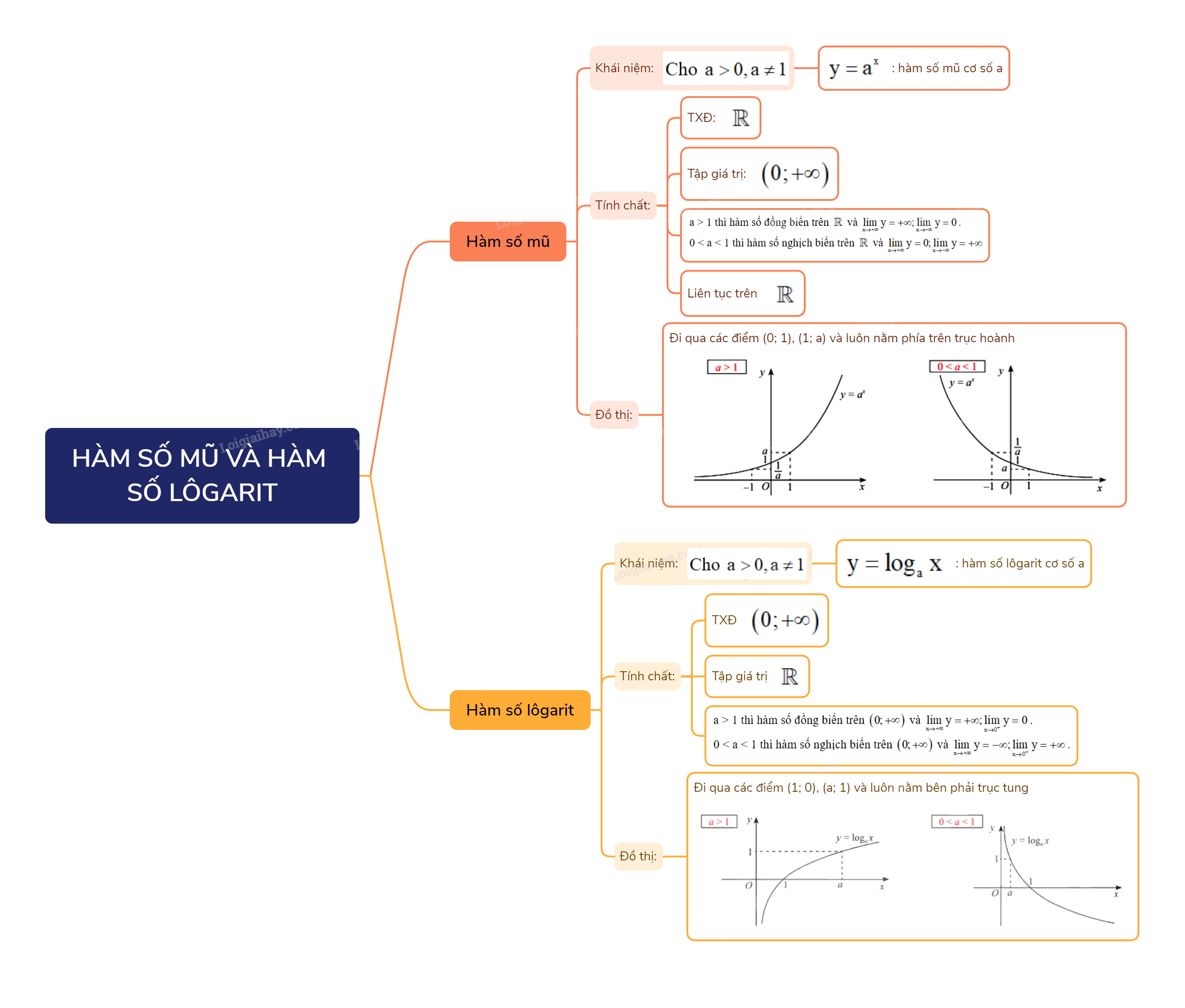
Chương trình Toán 11 Chân Trời Sáng Tạo đi sâu vào nghiên cứu về hàm số mũ và hàm số lôgarit, hai khái niệm then chốt trong toán học, có ứng dụng rộng rãi trong nhiều lĩnh vực khoa học và kỹ thuật. Bài viết này sẽ cung cấp một cái nhìn tổng quan và chi tiết về lý thuyết, tính chất, và các dạng bài tập thường gặp liên quan đến hai hàm số này.
1. Hàm Số Mũ
Hàm số mũ là hàm số có dạng y = ax, trong đó a là một số thực dương khác 1 (a > 0 và a ≠ 1). Hàm số mũ có những đặc điểm sau:
- Tập xác định: ℝ (tập hợp tất cả các số thực)
- Tập giá trị: (0, +∞)
- Tính đơn điệu:
- Nếu a > 1: Hàm số mũ đồng biến trên ℝ.
- Nếu 0 < a < 1: Hàm số mũ nghịch biến trên ℝ.
- Đồ thị: Đồ thị hàm số mũ luôn đi qua điểm (0, 1).
2. Hàm Số Lôgarit
Hàm số lôgarit là hàm số nghịch đảo của hàm số mũ. Hàm số lôgarit có dạng y = logax, trong đó a là một số thực dương khác 1 (a > 0 và a ≠ 1) và x > 0.
Hàm số lôgarit có những đặc điểm sau:
- Tập xác định: (0, +∞)
- Tập giá trị: ℝ
- Tính đơn điệu:
- Nếu a > 1: Hàm số lôgarit đồng biến trên (0, +∞).
- Nếu 0 < a < 1: Hàm số lôgarit nghịch biến trên (0, +∞).
- Đồ thị: Đồ thị hàm số lôgarit luôn đi qua điểm (1, 0).
3. Các Tính Chất Quan Trọng
Việc nắm vững các tính chất của hàm số mũ và hàm số lôgarit là rất quan trọng để giải các bài toán liên quan:
- loga(xy) = logax + logay
- loga(x/y) = logax - logay
- loga(xn) = n logax
- alogax = x
- logaa = 1
- loga1 = 0
4. Bài Tập Áp Dụng
Để củng cố kiến thức, hãy cùng giải một số bài tập ví dụ:
- Giải phương trình: 2x = 8
- Tính: log39
- Rút gọn biểu thức: log2(4x) - log2x
Lời khuyên: Hãy luyện tập thường xuyên và kết hợp với việc xem lại lý thuyết để nắm vững kiến thức về hàm số mũ và hàm số lôgarit. tusach.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán!
5. Ứng Dụng Thực Tế
Hàm số mũ và hàm số lôgarit có nhiều ứng dụng trong thực tế, ví dụ:
- Tăng trưởng dân số: Mô hình tăng trưởng dân số thường sử dụng hàm số mũ.
- Phân rã phóng xạ: Quá trình phân rã phóng xạ được mô tả bằng hàm số mũ.
- Đo cường độ âm thanh: Cường độ âm thanh được đo bằng decibel (dB), sử dụng hàm số lôgarit.
- Tính lãi kép: Công thức tính lãi kép sử dụng hàm số mũ.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về lý thuyết hàm số mũ và hàm số lôgarit lớp 11 Chân Trời Sáng Tạo. Chúc bạn học tập tốt!