Giải mục 2 trang 16 SGK Toán 11 tập 2 - Chân trời sáng tạo
Tổng quan nội dung
Giải Mục 2 Trang 16 SGK Toán 11 Tập 2 - Chân Trời Sáng Tạo
Chào mừng bạn đến với lời giải chi tiết Mục 2 trang 16 SGK Toán 11 tập 2, chương trình Chân trời sáng tạo. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp bạn hiểu sâu sắc kiến thức và tự tin làm bài tập.
tusach.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán.
Sử dụng máy tính cầm tay, tính giá trị các biểu thức sau (làm tròn kết quả đến chữ số thập phân thứ sáu):
Thực hành 2
Sử dụng máy tính cầm tay, tính giá trị các biểu thức sau (làm tròn kết quả đến chữ số thập phân thứ sáu):
a) \({\log _5}0,5\);
b) \(\log 25\);
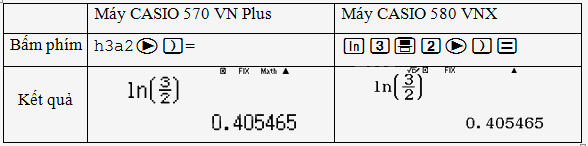
c) \(\ln \frac{3}{2}\).
Phương pháp giải:
Sử dụng máy tính cầm tay.
Lời giải chi tiết:
Để làm tròn đến chữ số thập phân thứ 6:

a,

b,

c,
Giải Mục 2 Trang 16 SGK Toán 11 Tập 2 - Chân Trời Sáng Tạo: Hướng Dẫn Chi Tiết
Mục 2 trang 16 SGK Toán 11 tập 2 Chân trời sáng tạo thường xoay quanh các bài toán về phép biến hình, đặc biệt là phép tịnh tiến, phép quay, và phép đối xứng. Việc nắm vững lý thuyết và phương pháp giải là yếu tố then chốt để giải quyết các bài tập này một cách hiệu quả.
1. Tóm Tắt Lý Thuyết Quan Trọng
Trước khi đi vào giải bài tập cụ thể, chúng ta cần ôn lại một số khái niệm và công thức quan trọng:
- Phép tịnh tiến: Biến hình bảo toàn khoảng cách giữa hai điểm bất kỳ.
- Phép quay: Biến hình bảo toàn khoảng cách giữa hai điểm bất kỳ và góc giữa hai đường thẳng bất kỳ.
- Phép đối xứng qua một điểm: Biến hình biến mỗi điểm M thành điểm M' sao cho I là trung điểm của đoạn thẳng MM'.
- Phép đối xứng qua một đường thẳng: Biến hình biến mỗi điểm M thành điểm M' sao cho đường thẳng d là đường trung trực của đoạn thẳng MM'.
2. Phân Tích Bài Tập Mục 2 Trang 16
Các bài tập trong Mục 2 thường yêu cầu:
- Xác định phép biến hình phù hợp để biến một hình cho trước thành một hình khác.
- Tìm tọa độ của điểm ảnh sau khi thực hiện phép biến hình.
- Chứng minh một hình là ảnh của một hình khác qua một phép biến hình.
3. Giải Chi Tiết Các Bài Tập (Ví dụ minh họa)
Bài 1: Cho điểm A(1; 2). Tìm tọa độ điểm A' là ảnh của A qua phép tịnh tiến theo vectơ v = (3; -1).
Lời giải:
Sử dụng công thức phép tịnh tiến: x' = x + vx, y' = y + vy
Vậy, x' = 1 + 3 = 4, y' = 2 + (-1) = 1
Do đó, A'(4; 1).
4. Mẹo Giải Bài Tập Nhanh Chóng
- Vẽ hình: Vẽ hình minh họa giúp bạn hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.
- Sử dụng công thức: Nắm vững các công thức liên quan đến phép biến hình.
- Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
5. Luyện Tập Thêm
Để củng cố kiến thức, bạn nên luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Việc thực hành thường xuyên sẽ giúp bạn nắm vững kiến thức và tự tin hơn khi làm bài kiểm tra.
6. Bảng Tham Khảo Công Thức Phép Biến Hình
| Phép Biến Hình | Công Thức |
|---|---|
| Tịnh Tiến | x' = x + vx, y' = y + vy |
| Quay | x' = x*cos(α) - y*sin(α), y' = x*sin(α) + y*cos(α) |
| Đối Xứng Qua Điểm I(a; b) | x' = 2a - x, y' = 2b - y |
Kết luận:
Hy vọng với hướng dẫn chi tiết này, bạn đã có thể tự tin giải các bài tập Mục 2 trang 16 SGK Toán 11 tập 2 Chân trời sáng tạo. Đừng ngần ngại liên hệ với tusach.vn nếu bạn cần thêm sự hỗ trợ!