Bài 8 trang 13 Toán 11 Tập 1 - Chân trời sáng tạo

Bài 8 trang 13 SGK Toán 11 tập 1 - Chân trời sáng tạo

Bài 8 trang 13 SGK Toán 11 Tập 1 - Chân trời sáng tạo

Bài 8 trang 13 SGK Toán 11 Tập 1 - Chân trời sáng tạo là bài tập thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng về giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán cụ thể.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

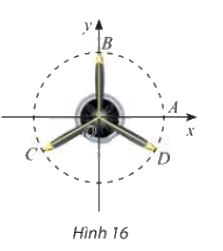
Vị trí các điểm B, C, D trên cánh quạt động cơ máy bay trong Hình 16 có thể được biểu diễn cho các góc lượng giác nào sau đây?

Đề bài

Vị trí các điểm B, C, D trên cánh quạt động cơ máy bay trong Hình 16 có thể được biểu diễn cho các góc lượng giác nào sau đây?

\(\frac{\pi }{2} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right);\frac{{ - \pi }}{6} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right);\frac{\pi }{2} + k\frac{\pi }{3}\,\,\left( {k \in \mathbb{Z}} \right)\)

Bài 8 trang 13 SGK Toán 11 tập 1 - Chân trời sáng tạo 1

Phương pháp giải - Xem chi tiết Bài 8 trang 13 SGK Toán 11 tập 1 - Chân trời sáng tạo 2

Quan sát hình vẽ, xác định góc lượng giác của điểm B, C, D.

Lời giải chi tiết

+ Xét góc lượng giác \(\frac{\pi }{2} + k\frac{{2\pi }}{3}\)

Với k = 0 thì \(\frac{\pi }{2} + 0.\frac{{2\pi }}{3} =\frac{\pi }{2} \) được biểu diễn bởi điểm B.

Với k = 1 thì \(\frac{\pi }{2} + 1.\frac{{2\pi }}{3} =\frac{7\pi }{6} \) được biểu diễn bởi điểm C.

Với k = 2 thì \(\frac{\pi }{2} + 2.\frac{{2\pi }}{3} =\frac{11\pi }{6} \) được biểu diễn bởi điểm D.

+ Xét góc lượng giác \(\frac{\pi }{2} + k\frac{\pi }{3}\,\,\left( {k \in \mathbb{Z}} \right)\)

Với k = 0 thì \(\frac{\pi }{2} + 0.\frac{{\pi }}{3} =\frac{\pi }{2} \) được biểu diễn bởi điểm B.

Với k = 1 thì \(\frac{\pi }{2} + 1.\frac{{\pi }}{3} =\frac{5\pi }{6} \) không biểu diễn bởi điểm nào.

+ Xét góc lượng giác \(\frac{{ - \pi }}{6} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right)\)

Với k = 1 thì \(\frac{{ - \pi }}{6}+ 1.\frac{{2\pi }}{3} =\frac{\pi }{2} \) được biểu diễn bởi điểm B.

Với k = 2 thì \(\frac{{ - \pi }}{6}+ 2.\frac{{2\pi }}{3} =\frac{7\pi }{6} \) được biểu diễn bởi điểm C.

Với k = 3 thì \(\frac{{ - \pi }}{6} + 3.\frac{{2\pi }}{3} =\frac{11\pi }{6} \) được biểu diễn bởi điểm D.

Vậy các điểm B, C, D trên cánh quạt động cơ máy bay trong Hình 16 có thể được biểu diễn cho các góc lượng giác

\(\frac{\pi }{2} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right);\frac{{ - \pi }}{6} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right)\,\,\left( {k \in \mathbb{Z}} \right)\)

Bài 8 trang 13 SGK Toán 11 Tập 1 - Chân trời sáng tạo: Giải chi tiết và hướng dẫn

Bài 8 trang 13 SGK Toán 11 Tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh củng cố kiến thức về giới hạn của hàm số. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:

Nội dung bài tập

Bài 8 yêu cầu tính các giới hạn sau:

lim (x→2) (x^2 - 3x + 2) / (x - 2)
lim (x→-1) (x^3 + 1) / (x + 1)
lim (x→0) (√(x+1) - 1) / x
lim (x→1) (x^n - 1) / (x - 1)

Lời giải chi tiết

1. lim (x→2) (x^2 - 3x + 2) / (x - 2)

Ta có thể phân tích tử thức thành (x - 1)(x - 2). Do đó:

lim (x→2) (x^2 - 3x + 2) / (x - 2) = lim (x→2) (x - 1)(x - 2) / (x - 2) = lim (x→2) (x - 1) = 2 - 1 = 1

2. lim (x→-1) (x^3 + 1) / (x + 1)

Ta có thể phân tích tử thức thành (x + 1)(x^2 - x + 1). Do đó:

lim (x→-1) (x^3 + 1) / (x + 1) = lim (x→-1) (x + 1)(x^2 - x + 1) / (x + 1) = lim (x→-1) (x^2 - x + 1) = (-1)^2 - (-1) + 1 = 3

3. lim (x→0) (√(x+1) - 1) / x

Để khử dạng vô định, ta nhân cả tử và mẫu với liên hợp của tử thức: (√(x+1) + 1)

lim (x→0) (√(x+1) - 1) / x = lim (x→0) [(√(x+1) - 1)(√(x+1) + 1)] / [x(√(x+1) + 1)] = lim (x→0) (x+1 - 1) / [x(√(x+1) + 1)] = lim (x→0) x / [x(√(x+1) + 1)] = lim (x→0) 1 / (√(x+1) + 1) = 1 / (√(0+1) + 1) = 1/2

4. lim (x→1) (x^n - 1) / (x - 1)

Đây là một giới hạn quen thuộc, có thể sử dụng công thức giới hạn đặc biệt: lim (x→a) (x^n - a^n) / (x - a) = n*a^(n-1)

Trong trường hợp này, a = 1, do đó: lim (x→1) (x^n - 1) / (x - 1) = n*1^(n-1) = n

Lưu ý quan trọng

Khi tính giới hạn, cần chú ý đến các dạng vô định và sử dụng các phương pháp phù hợp để khử dạng vô định.
Nắm vững các công thức giới hạn đặc biệt để giải quyết nhanh chóng các bài tập.
Kiểm tra lại kết quả sau khi tính toán để đảm bảo tính chính xác.

Bài tập tương tự

Để rèn luyện thêm kỹ năng giải bài tập về giới hạn, bạn có thể tham khảo các bài tập tương tự trong SGK Toán 11 Tập 1 - Chân trời sáng tạo và các tài liệu ôn tập khác.

tusach.vn hy vọng với lời giải chi tiết này, bạn sẽ hiểu rõ hơn về cách giải Bài 8 trang 13 SGK Toán 11 Tập 1 - Chân trời sáng tạo và tự tin hơn trong quá trình học tập.