Bài 4 trang 56 SGK Toán 11 tập 2 – Chân trời sáng tạo

Tổng quan nội dung

Bài 4 trang 56 SGK Toán 11 tập 2 – Chân trời sáng tạo

Bài 4 trang 56 SGK Toán 11 tập 2 thuộc chương trình Toán 11 Chân trời sáng tạo, tập trung vào việc ôn tập về đạo hàm. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế liên quan đến đạo hàm của hàm số.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.

Cho tứ diện đều (ABCD) cạnh (a). Gọi (K) là trung điểm của (CD).

Đề bài

Cho tứ diện đều \(ABCD\) cạnh \(a\). Gọi \(K\) là trung điểm của \(CD\). Tính góc giữa hai đường thẳng \(AK\) và \(BC\).

Phương pháp giải - Xem chi tiết Bài 4 trang 56 SGK Toán 11 tập 2 – Chân trời sáng tạo 1

Cách xác định góc giữa hai đường thẳng \(a\) và \(b\):

Bước 1: Lấy một điểm \(O\) bất kì.

Bước 2: Qua điểm \(O\) dựng đường thẳng \(a'\parallel a\) và đường thẳng \(b'\parallel b\).

Bước 3: Tính \(\left( {a,b} \right) = \left( {a',b'} \right)\).

Lời giải chi tiết

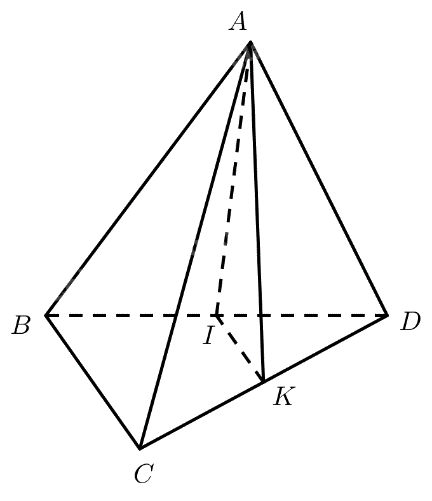
Bài 4 trang 56 SGK Toán 11 tập 2 – Chân trời sáng tạo 2

Gọi \(I\) là trung điểm của \(B{\rm{D}}\).

Ta có: \(I\) là trung điểm của \(B{\rm{D}}\)

\(K\) là trung điểm của \(CD\)

\( \Rightarrow IK\) là đường trung bình của tam giác \(BCD\)

\( \Rightarrow IK\parallel BC \Rightarrow \left( {AK,BC} \right) = \left( {AK,IK} \right) = \widehat {AKI}\)

\(IK = \frac{1}{2}BC = \frac{a}{2}\)

\(AI\) là trung tuyến của tam giác \(AB{\rm{D}}\)\( \Rightarrow AI = \frac{{\sqrt {2\left( {A{B^2} + A{{\rm{D}}^2}} \right) - B{{\rm{D}}^2}} }}{2} = \frac{{a\sqrt 3 }}{2}\)

\(AK\) là trung tuyến của tam giác \(AC{\rm{D}}\)\( \Rightarrow AK = \frac{{\sqrt {2\left( {A{C^2} + A{{\rm{D}}^2}} \right) - C{{\rm{D}}^2}} }}{2} = \frac{{a\sqrt 3 }}{2}\)

Xét tam giác \(AIK\) có:

\(\cos \widehat {AKI} = \frac{{A{K^2} + I{K^2} - A{I^2}}}{{2.AK.IK}} = \frac{{\sqrt 3 }}{6} \Rightarrow \widehat {AKI} \approx {73^ \circ }13'\)

Vậy \(\left( {AK,BC} \right) \approx {73^ \circ }13'\).

Bài 4 trang 56 SGK Toán 11 tập 2 – Chân trời sáng tạo: Giải chi tiết và hướng dẫn

Bài 4 trang 56 SGK Toán 11 tập 2 – Chân trời sáng tạo là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:

Nội dung bài tập

Bài 4 yêu cầu học sinh thực hiện các nhiệm vụ sau:

Tính đạo hàm của các hàm số đã cho.
Xác định các điểm mà tại đó hàm số không có đạo hàm.
Vận dụng đạo hàm để giải các bài toán liên quan đến tiếp tuyến của đồ thị hàm số.

Lời giải chi tiết

Để giải bài 4 trang 56 SGK Toán 11 tập 2, chúng ta cần nắm vững các quy tắc tính đạo hàm cơ bản, bao gồm:

Đạo hàm của hàm số lũy thừa: (xⁿ)' = nx^n-1
Đạo hàm của hàm số lượng giác: (sin x)' = cos x, (cos x)' = -sin x
Đạo hàm của hàm số mũ và logarit: (e^x)' = e^x, (ln x)' = 1/x
Quy tắc đạo hàm của tổng, hiệu, tích và thương của các hàm số.

Ví dụ: Giả sử hàm số f(x) = x² + sin x. Để tính đạo hàm của f(x), ta áp dụng quy tắc đạo hàm của tổng và đạo hàm của hàm số lũy thừa và hàm số lượng giác:

f'(x) = (x²)' + (sin x)' = 2x + cos x

Các dạng bài tập thường gặp

Trong bài 4 trang 56 SGK Toán 11 tập 2, học sinh có thể gặp các dạng bài tập sau:

Dạng 1: Tính đạo hàm của hàm số đơn giản.
Dạng 2: Tính đạo hàm của hàm số hợp.
Dạng 3: Tìm điểm mà tại đó hàm số không có đạo hàm (ví dụ: điểm không xác định, điểm gián đoạn).
Dạng 4: Vận dụng đạo hàm để tìm tiếp tuyến của đồ thị hàm số.

Mẹo giải bài tập

Để giải bài tập về đạo hàm hiệu quả, học sinh nên:

Nắm vững các quy tắc tính đạo hàm cơ bản.
Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Kiểm tra lại kết quả sau khi tính đạo hàm.
Sử dụng máy tính bỏ túi để kiểm tra kết quả.

Bài tập tương tự

Để rèn luyện thêm kỹ năng giải bài tập về đạo hàm, học sinh có thể tham khảo các bài tập tương tự trong SGK Toán 11 tập 2 và các tài liệu ôn tập khác.

Kết luận

Bài 4 trang 56 SGK Toán 11 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Bằng cách nắm vững các quy tắc tính đạo hàm và luyện tập thường xuyên, học sinh có thể giải quyết bài tập này một cách hiệu quả.

Hàm số	Đạo hàm
f(x) = x³	f'(x) = 3x²
g(x) = sin(2x)	g'(x) = 2cos(2x)