1. Góc giữa hai mặt phẳng
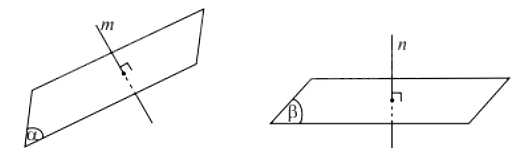
Góc giữa hai mặt phẳng \(\left( \alpha \right)\)và \(\left( \beta \right)\) là góc giữa hai đường thẳng lần lượt vuông góc với \(\left( \alpha \right)\)và \(\left( \beta \right)\), kí hiệu \(\left( {\;\left( \alpha \right),\left( \beta \right)} \right)\).
Ta có: \(\left( {\;\left( \alpha \right),\left( \beta \right)} \right) = \left( {m,n} \right)\) với \(m \bot \left( \alpha \right),n \bot \left( \beta \right)\).
2. Hai mặt phẳng vuông góc
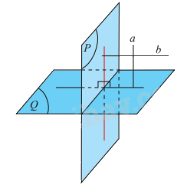
Hai mặt phẳng được gọi là vuông góc với nhau nếu góc giữa hai mặt phẳng đó là một góc vuông.
Hai mặt phẳng (P) và (Q) vuông góc được kí hiệu là \(\left( P \right) \bot \left( Q \right)\).
3. Điều kiện để hai mặt phẳng vuông góc
Định lí 1:
Điều kiện cần và đủ để hai mặt phẳng vuông góc là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
4. Tính chất cơ bản về hai mặt phẳng vuông góc
Định lí 2:
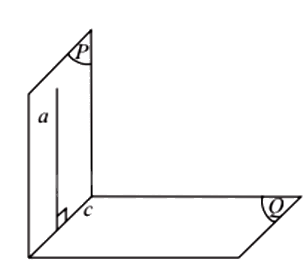
Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào nằm trong mặt phẳng này và vuông góc với giao tuyến cũng vuông góc với mặt phẳng kia.
Định lí 3:
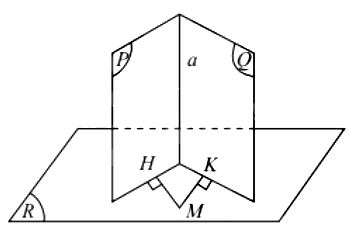
Nếu hai mặt phẳng cắt nhau và cùng vuông góc với một mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba đó.
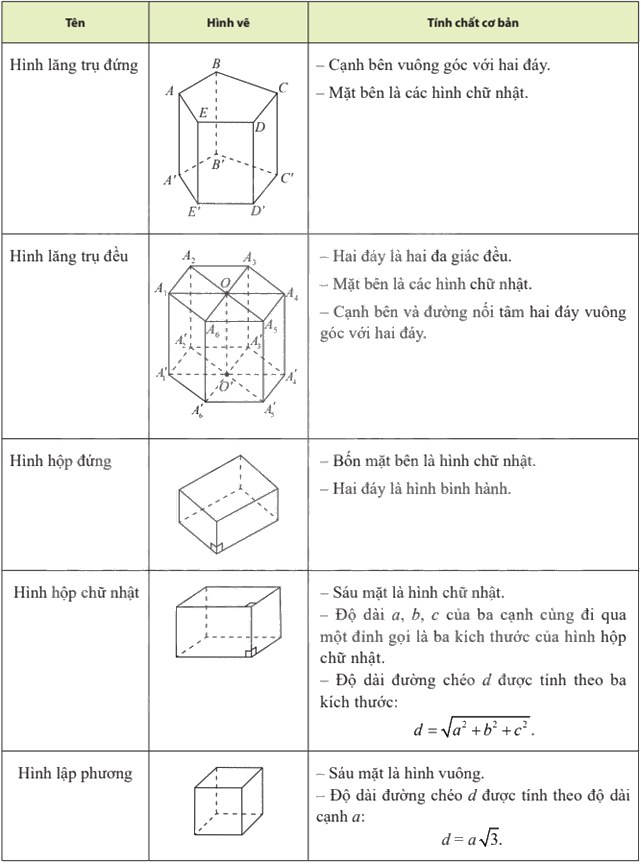
5. Hình lăng trụ đứng, hình hộp chữ nhật, hình lập phương
Hình lăng trụ đứng là hình lăng trụ có cạnh bên vuông góc với mặt đáy.
Hình lăng trụ đều là hình lăng trụ đúng có mặt đáy là đa giác đều.
Hình hộp đứng là hình hộp có cạnh bên vuông góc với mặt đáy.
Hình hộp chữ nhật là hình hộp đứng có mặt đáy là hình chữ nhật.
Hình lập phương là hình hộp chữ nhật có tất cả các cạnh bằng nhau.
6. Hình chóp đều. Hình chóp cụt đều
a) Hình chóp đều
Hình chóp đều là hình chóp có đáy là đa giác đều và các cạnh bên bằng nhau.
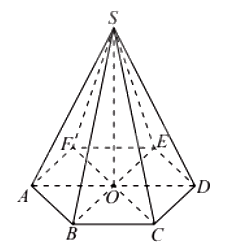
Chú ý: Hình chóp đều có:
- Các mặt bên là các tam giác cân tại đỉnh hình chóp và bằng nhau.
- Đoạn thẳng nối từ đỉnh hình chóp đến tâm của đáy thì vuông góc với mặt đáy và gọi là đường cao của hình chóp.
- Độ dài đường cao gọi là chiều cao của hình chóp đều.
b) Hình chóp cụt đều
Phần của hình chóp đều nằm giữa đáy và một mặt phẳng song song với đáy cắt các cạnh bên của hình chóp đều được gọi là hình chóp cụt đều.
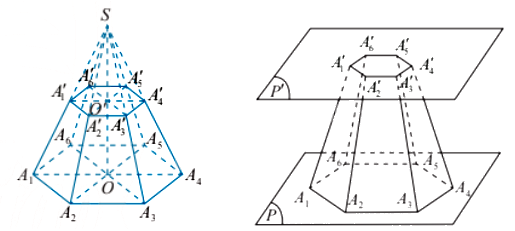
Trong hình chóp cụt đều \({A_1}{A_2} \ldots {A_6}.A{'_1}A{'_2} \ldots A{'_6}\), ta gọi:
- Các điểm \({A_1},{A_2}, \ldots ,{A_6},A{'_1},A{'_2}, \ldots ,A{'_6}\) là các đỉnh.
\({A_1}{A_2}{B_2}{B_1},{A_2}{A_3}{B_3}{B_2}, \ldots ,{A_n}{A_1}{B_1}{B_n}\) được gọi là một hình chóp cụt đều (nói đơn giản là hình chóp cụt được tạo thành từ hình chóp đều \(S.{A_1}{A_2} \ldots {A_n}\) sau khi cắt đi chóp đều \(S \cdot {B_1}{B_2} \ldots {B_n}\)), kí hiệu là \({A_1}{A_2} \ldots {A_n} \cdot {B_1}{B_2} \ldots {B_n}\).
- Đa giác \({A_1}{A_2} \ldots {A_6}\) là đáy lớn, đa giác \(A{'_1}A{'_2}A{'_3}...A{'_6}\) là đáy nhỏ. Đáy lớn và đáy nhỏ nằm trên hai mặt phẳng song song.
- Cạnh của hai đa giác đáy là cạnh đáy. Các cạnh tương ứng song song từng đôi một.
- Các hình thang cân \({A_1}{A_2}A{'_2}A{'_1},{A_2}{A_3}A{'_3}A{'_2}, \ldots ,{A_6}{A_1}A{'_1}A'6\) được gọi là các mặt bên.
- Cạnh bên của mặt bên gọi là cạnh bên của hình chóp cụt đều. Hình chóp cụt đều có các cạnh bên bằng nhau, các mặt bên là những hình thang cân.
- Đoạn thẳng nối tâm hai đáy là đường cao. Độ dài đường cao là chiều cao.
