Lý thuyết Đạo hàm - Toán 11 Chân trời sáng tạo
Tổng quan nội dung
Lý thuyết Đạo hàm - Toán 11 Chân trời sáng tạo
Chào mừng bạn đến với chuyên mục Lý thuyết Đạo hàm của chương trình Toán 11 Chân trời sáng tạo tại tusach.vn!
Đạo hàm là một khái niệm nền tảng quan trọng trong chương trình Toán học, đặc biệt là trong giai đoạn học THPT.
Nội dung bài viết này sẽ cung cấp một cách đầy đủ, dễ hiểu về lý thuyết đạo hàm, các công thức tính đạo hàm cơ bản và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế.
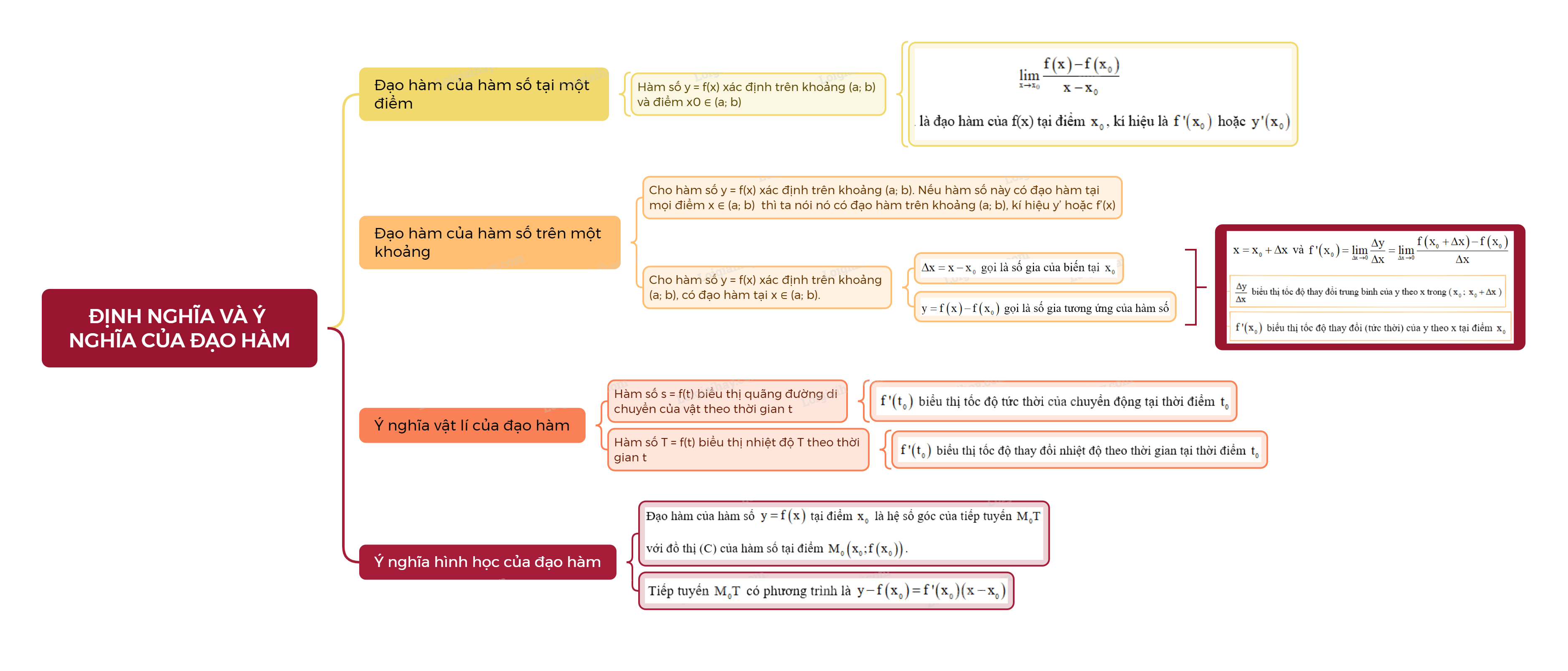
1. Đạo hàm Cho hàm số y = f(x) xác định trên khoảng \(\left( {a;b} \right)\) và điểm \({x_0} \in \left( {a;b} \right)\).
1. Đạo hàm
Cho hàm số y = f(x) xác định trên khoảng \(\left( {a;b} \right)\) và điểm \({x_0} \in \left( {a;b} \right)\).
Nếu tồn tại giới hạn (hữu hạn)
\(\mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\)
thì giới hạn đó được gọi là đạo hàm của f(x) tại điểm \({x_0}\), kí hiệu là \(f'\left( {{x_0}} \right)\) hoặc \(y'\left( {{x_0}} \right)\).
Vậy:
\(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\).
Chú ý:
- Cho hàm số y = f(x) xác định trên khoảng (a; b). Nếu hàm số này có đạo hàm tại mọi điểm \(x \in \left( {a;b} \right)\) thì ta nói nó có đạo hàm trên khoảng (a; b), kí hiệu y’ hoặc f’(x).
- Cho hàm số y = f(x) xác định trên khoảng (a; b), có đạo hàm tại \({x_0} \in \left( {a;b} \right)\).
a) Đại lượng \(\Delta x = x - {x_0}\) gọi là số gia của biến tại \({x_0}\). Đại lượng \(y = f\left( x \right) - f\left( {{x_0}} \right)\) gọi là số gia tương ứng của hàm số. Khi đó, \(x = {x_0} + \Delta x\) và
\(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{f\left( {{x_0} + \Delta x} \right) - f\left( {{x_0}} \right)}}{{\Delta x}}\).
b) Tỉ số \(\frac{{\Delta y}}{{\Delta x}}\) biểu thị tốc độ thay đổi trung bình của đại lượng y theo đại lượng x trong khoảng từ \({x_0}\) đến \({x_0} + \Delta x\); còn \(f'\left( {{x_0}} \right)\) biểu thị tốc độ thay đổi (tức thời) của đại lượng y theo đại lượng x tại điểm \({x_0}\).
2. Ý nghĩa vật lí của đạo hàm
- Nếu hàm số s = f(t) biểu thị quãng đường di chuyển của vật theo thời gian t thì \(f'\left( {{t_0}} \right)\) biểu thị tốc độ tức thời của chuyển động tại thời điểm \({t_0}\).
- Nếu hàm số T = f(t) biểu thị nhiệt độ T theo thời gian t thì \(f'\left( {{t_0}} \right)\) biểu thị tốc độ thay đổi nhiệt độ theo thời gian tại thời điểm \({t_0}\).
3. Ý nghĩa hình học của đạo hàm
Đạo hàm của hàm số \(y = f\left( x \right)\) tại điểm \({x_0}\) là hệ số góc của tiếp tuyến \({M_0}T\) với đồ thị (C) của hàm số tại điểm \({M_0}\left( {{x_0};f\left( {{x_0}} \right)} \right)\).
Tiếp tuyến \({M_0}T\) có phương trình là \(y - f\left( {{x_0}} \right) = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right)\).
Lý Thuyết Đạo Hàm - Toán 11 Chân Trời Sáng Tạo: Tổng Quan Chi Tiết
Chào mừng các em học sinh đến với bài viết tổng hợp lý thuyết đạo hàm Toán 11 Chân trời sáng tạo. Đây là một trong những chủ đề quan trọng bậc nhất của chương trình Toán 11, đóng vai trò nền tảng cho các kiến thức nâng cao hơn trong các lớp học tiếp theo và trong kỳ thi THPT Quốc gia.
1. Khái Niệm Đạo Hàm
Đạo hàm của hàm số f(x) tại điểm x0, ký hiệu là f'(x0), biểu thị tốc độ thay đổi tức thời của hàm số tại điểm đó. Về mặt hình học, đạo hàm là hệ số góc của tiếp tuyến của đồ thị hàm số tại điểm x0.
Công thức tính đạo hàm theo định nghĩa:
f'(x0) = limΔx→0 [f(x0 + Δx) - f(x0)] / Δx
2. Các Quy Tắc Tính Đạo Hàm
Để việc tính đạo hàm trở nên dễ dàng hơn, chúng ta sử dụng các quy tắc sau:
- Quy tắc đạo hàm của hàm số lũy thừa: (xn)' = nxn-1
- Quy tắc đạo hàm của hàm số đa thức: (u + v)' = u' + v'
- Quy tắc đạo hàm của tích hai hàm số: (uv)' = u'v + uv'
- Quy tắc đạo hàm của thương hai hàm số: (u/v)' = (u'v - uv') / v2
- Quy tắc đạo hàm của hàm hợp: (f(g(x)))' = f'(g(x)) * g'(x)
3. Đạo Hàm Của Một Số Hàm Số Cơ Bản
| Hàm số | Đạo hàm |
|---|---|
| f(x) = c (hằng số) | f'(x) = 0 |
| f(x) = x | f'(x) = 1 |
| f(x) = xn | f'(x) = nxn-1 |
| f(x) = sin(x) | f'(x) = cos(x) |
| f(x) = cos(x) | f'(x) = -sin(x) |
4. Ứng Dụng Của Đạo Hàm
Đạo hàm có rất nhiều ứng dụng trong toán học và các lĩnh vực khác:
- Tìm cực trị của hàm số: Đạo hàm bằng 0 tại các điểm cực trị.
- Khảo sát sự biến thiên của hàm số: Xác định khoảng đồng biến, nghịch biến của hàm số.
- Giải các bài toán tối ưu: Tìm giá trị lớn nhất, nhỏ nhất của hàm số trong một khoảng cho trước.
- Tính vận tốc và gia tốc: Trong vật lý, đạo hàm của quãng đường theo thời gian là vận tốc, và đạo hàm của vận tốc theo thời gian là gia tốc.
5. Bài Tập Vận Dụng (Ví dụ)
Bài 1: Tính đạo hàm của hàm số f(x) = 3x2 + 2x - 1
Giải:
f'(x) = 6x + 2
Bài 2: Tìm đạo hàm của hàm số f(x) = sin(2x)
Giải:
f'(x) = 2cos(2x) (Sử dụng quy tắc đạo hàm hàm hợp)
Kết Luận
Hy vọng bài viết này đã cung cấp cho các em một cái nhìn tổng quan và đầy đủ về lý thuyết đạo hàm Toán 11 Chân trời sáng tạo. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin giải quyết các bài toán liên quan đến đạo hàm. Chúc các em học tốt!