Lý thuyết Điểm, đường thẳng và mặt phẳng trong không gian - SGK Toán 11 Chân trời sáng tạo
Tổng quan nội dung
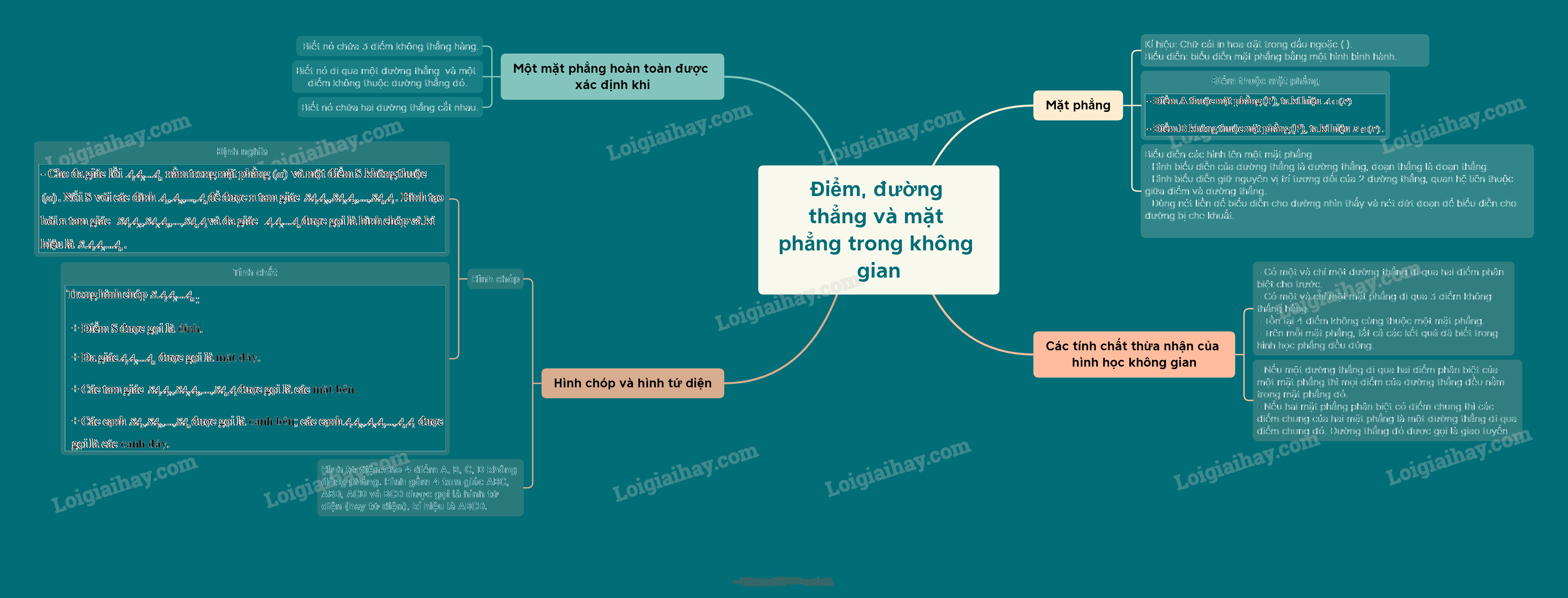
Lý thuyết Điểm, Đường thẳng và Mặt phẳng trong không gian - Nền tảng Toán 11
Đây là một trong những chủ đề quan trọng của chương trình Hình học không gian lớp 11, thuộc SGK Toán 11 Chân trời sáng tạo.
Nắm vững kiến thức về điểm, đường thẳng và mặt phẳng là bước đệm quan trọng để giải quyết các bài toán phức tạp hơn về quan hệ không gian.
Tusach.vn cung cấp tài liệu học tập đầy đủ, dễ hiểu, giúp bạn chinh phục chủ đề này một cách hiệu quả.
1. Mặt phẳng
1. Mặt phẳng

Hình ảnh mặt phẳng trong thực tiễn
- Biểu diễn một mặt phẳng: Người ta thường biểu diễn mặt phẳng bằng một hình bình hành.
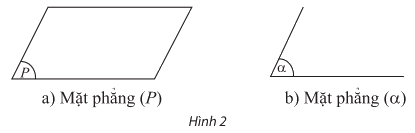
- Để kí hiệu mặt phẳng ta dùng chữ cái in hoa đặt trong dấu ngoặc ( ). Mặt phẳng (P) còn được viết là mp(P) hay (P).
* Điểm thuộc mặt phẳng
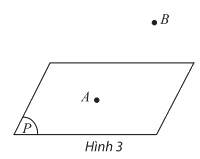
- Điểm A thuộc mặt phẳng (P) thì ta nói A nằm trên (P) hay (P) chứa A, ta kí hiệu \(A \in (P)\)
- Điểm B không thuộc mặt phẳng (P) thì ta nói B nằm ngoài (P) hay (P) không chứa B, ta kí hiệu \(B \notin (P)\).
* Biểu diễn các hình lên một mặt phẳng
- Hình biểu diễn của đường thẳng là đường thẳng, của đoạn thẳng là đoạn thẳng.
- Hình biểu diễn của hai đường thẳng song song là 2 đường thẳng song song, của 2 đường thẳng cắt nhau là 2 đường thẳng cắt nhau.
- Hình biểu diễn giữ nguyên quan hệ liên thuộc giữa điểm và đường thẳng.
- Dùng nét liền để biểu diễn cho đường nhìn thấy và nét đứt đoạn để biểu diễn cho đường bị che khuất.
2. Các tính chất thừa nhận của hình học không gian
- Có một và chỉ một đường thẳng đi qua hai điểm phân biệt cho trước.
- Có một và chỉ một mặt phẳng đi qua 3 điểm không thẳng hàng.
- Nếu một đường thẳng đi qua hai điểm phân biệt của một mặt phẳng thì mọi điểm của đường thẳng đều nằm trong mặt phẳng đó.
- Tồn tại 4 điểm không cùng thuộc một mặt phẳng.
- Nếu mọi điểm của đường thẳng d đều thuộc mặt phẳng (P) thì ta nói d nằm trong (P) hoặc (P) chứa d. Kí hiệu \(d \subset (P)\) hoặc \((P) \supset d\).
- Nếu hai mặt phẳng phân biệt có điểm chung thì các điểm chung của hai mặt phẳng là một đường thẳng đi qua điểm chung đó. Đường thẳng đó được gọi là giao tuyến, kí hiệu \(d = (\alpha ) \cap (\beta )\).
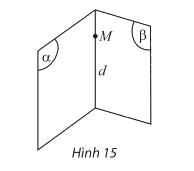
- Trên mỗi mặt phẳng, tất cả các kết quả đã biết trong hình học phẳng đều đúng.
3. Cách xác định mặt phẳng
- Một mặt phẳng hoàn toàn được xác định khi biết nó chứa 3 điểm không thẳng hàng.
- Một mặt phẳng được hoàn toàn xác định khi biết nó đi qua một đường thẳng và một điểm không thuộc đường thẳng đó.
- Một mặt phẳng được hoàn toàn xác định nếu biết nó chứa hai đường thẳng cắt nhau.
4. Hình chóp và hình tứ diện
- Hình chóp
- Cho đa giác lồi \({A_1}{A_2}...{A_n}\) nằm trong mặt phẳng \((\alpha )\) và một điểm S không thuộc \((\alpha )\). Nối S với các đỉnh \({A_1},{A_2},...,{A_n}\)để được n tam giác \(S{A_1}{A_2},S{A_2}{A_3},...,S{A_n}{A_1}\). Hình tạo bởi n tam giác \(S{A_1}{A_2},S{A_2}{A_3},...,S{A_n}{A_1}\)và đa giác \({A_1}{A_2}...{A_n}\)được gọi là hình chóp và kí hiệu là \(S.{A_1}{A_2}...{A_n}\).
- Trong hình chóp \(S.{A_1}{A_2}...{A_n}\):
+ Điểm S được gọi là đỉnh.
+ Đa giác\({A_1}{A_2}...{A_n}\) được gọi là mặt đáy.
+ Các tam giác \(S{A_1}{A_2},S{A_2}{A_3},...,S{A_n}{A_1}\)được gọi là các mặt bên
+ Các cạnh \(S{A_1},S{A_2},...,S{A_n}\)được gọi là cạnh bên; các cạnh\({A_1}{A_2},{A_2}{A_3}...,{A_n}{A_1}\) được gọi là các cạnh đáy.
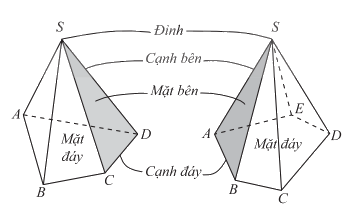
* Nếu đáy của hình chóp là một tam giác, tứ giác, ngũ giác,…thì hình chóp tương ứng gọi là hình chóp tam giác, hình chóp tứ giác, hình chóp ngũ giác,…
- Hình tứ diện
Cho 4 điểm A, B, C, D không đồng phẳng. Hình gồm 4 tam giác ABC, ABD, ACD và BCD được gọi là hình tứ diện (hay tứ diện), kí hiệu là ABCD.
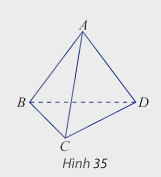
Trong đó, các điểm A, B, C, D được gọi các đỉnh của tứ diện, các đoạn thẳng AB, BC, CD, DA, BD,AC được gọi là cạnh của tứ diện; các tam giác ABC, ABD, ACD và BCD gọi là mặt của tứ diện.
Hai cạnh không có đỉnh chung được gọi là hai cạnh đối diện, đỉnh không nằm trên một mặt gọi là đỉnh đối diện với mặt đó.
Lý Thuyết Điểm, Đường Thẳng và Mặt Phẳng trong Không Gian - SGK Toán 11 Chân Trời Sáng Tạo
Chương trình Toán 11 Chân Trời Sáng Tạo đi sâu vào kiến thức về hình học không gian, và một trong những nền tảng quan trọng nhất là lý thuyết về điểm, đường thẳng và mặt phẳng trong không gian. Bài viết này sẽ cung cấp một cái nhìn tổng quan và chi tiết về các khái niệm, định lý và ứng dụng của chủ đề này.
1. Các Khái Niệm Cơ Bản
- Điểm: Là một thực thể hình học không có kích thước.
- Đường thẳng: Là tập hợp các điểm liên tiếp nhau trên một đường không cong.
- Mặt phẳng: Là tập hợp các điểm thỏa mãn một điều kiện nhất định.
Để hiểu rõ hơn, ta có thể hình dung một điểm như một chấm nhỏ, đường thẳng như một sợi chỉ căng thẳng, và mặt phẳng như một tờ giấy phẳng.
2. Quan Hệ Giữa Các Điểm và Đường Thẳng
Có ba trường hợp xảy ra giữa một điểm và một đường thẳng:
- Điểm nằm trên đường thẳng.
- Điểm không nằm trên đường thẳng.
Để xác định một đường thẳng, ta cần tối thiểu hai điểm phân biệt.
3. Quan Hệ Giữa Các Mặt Phẳng
Có ba trường hợp xảy ra giữa hai mặt phẳng:
- Hai mặt phẳng song song.
- Hai mặt phẳng cắt nhau.
- Hai mặt phẳng trùng nhau.
Hai mặt phẳng song song là hai mặt phẳng không có điểm chung. Hai mặt phẳng cắt nhau là hai mặt phẳng có một đường thẳng chung. Hai mặt phẳng trùng nhau là hai mặt phẳng có tất cả các điểm chung.
4. Quan Hệ Giữa Điểm và Mặt Phẳng
Có hai trường hợp xảy ra giữa một điểm và một mặt phẳng:
- Điểm nằm trên mặt phẳng.
- Điểm không nằm trên mặt phẳng.
5. Các Định Lý Quan Trọng
Một số định lý quan trọng cần nắm vững:
- Định lý 1: Nếu một đường thẳng nằm trên một mặt phẳng thì mọi điểm của đường thẳng đều nằm trên mặt phẳng đó.
- Định lý 2: Nếu hai mặt phẳng có một điểm chung thì chúng có vô số điểm chung nằm trên một đường thẳng.
6. Ứng Dụng của Lý Thuyết
Lý thuyết về điểm, đường thẳng và mặt phẳng trong không gian có ứng dụng rộng rãi trong nhiều lĩnh vực, bao gồm:
- Kiến trúc: Thiết kế các công trình xây dựng.
- Kỹ thuật: Xây dựng các mô hình 3D.
- Vật lý: Mô tả các hiện tượng trong không gian.
7. Bài Tập Vận Dụng
Để củng cố kiến thức, hãy giải các bài tập sau:
| Bài tập | Đáp án |
|---|---|
| Cho hai điểm A và B. Xác định đường thẳng đi qua hai điểm này. | Vẽ một đường thẳng nối hai điểm A và B. |
| Cho một điểm M và một mặt phẳng (P). Xác định vị trí của điểm M so với mặt phẳng (P). | Điểm M có thể nằm trên mặt phẳng (P) hoặc không nằm trên mặt phẳng (P). |
Kết luận: Việc nắm vững lý thuyết về điểm, đường thẳng và mặt phẳng trong không gian là vô cùng quan trọng để học tốt môn Toán 11 Chân Trời Sáng Tạo. Hãy dành thời gian ôn tập và luyện tập thường xuyên để đạt kết quả tốt nhất.
Tusach.vn hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích và giúp bạn tự tin hơn trong việc học tập.