Giải mục 2 trang 122, 123, 124 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 2 trang 122, 123, 124 SGK Toán 11 tập 1 - Chân trời sáng tạo
Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 122, 123, 124 SGK Toán 11 tập 1 chương trình Chân trời sáng tạo. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài toán và đạt kết quả cao trong môn Toán.
Trong Hình 4, xét phép chiếu theo phương (l) lên mặt phẳng (left( P right)), mặt phẳng (left( Q right)) chứa đường thẳng (a) và song song với phương chiếu
Hoạt động 2
Trong Hình 4, xét phép chiếu theo phương \(l\) lên mặt phẳng \(\left( P \right)\), mặt phẳng \(\left( Q \right)\) chứa đường thẳng \(a\) và song song với phương chiếu.
a) Khi điểm \(M\) thay đổi trên đường thẳng \(a\) thì ảnh \(M'\) của nó thay đổi ở đâu?
b) Từ đó hãy chỉ ra ảnh của đường thẳng \(a\) qua phép chiếu theo phương \(l\) lên mặt phẳng \(\left( P \right)\).
Phương pháp giải:
Quan sát hình ảnh và trả lời câu hỏi.
Lời giải chi tiết:
a) Khi điểm \(M\) thay đổi trên đường thẳng \(a\) thì ảnh \(M'\) của nó thay đổi trên đường thẳng \(a'\).
b) Ảnh của đường thẳng \(a\) qua phép chiếu theo phương \(l\) lên mặt phẳng \(\left( P \right)\) là đường thẳng \(a'\).
Hoạt động 3
Trong Hình 5, xét phép chiếu theo phương \(l\) với mặt phẳng chiếu \(\left( P \right)\). Biết \(a\parallel b\) với \(a \subset \left( Q \right)\) và \(b \subset \left( R \right)\). Nêu nhận xét về vị trí tương đối của hình chiếu \(a',b'\) của \(a,b\) trong hai trường hợp: \(\left( Q \right)\parallel \left( R \right);\left( Q \right) \equiv \left( R \right)\).

Phương pháp giải:
‒ Quan sát hình ảnh và trả lời câu hỏi.
‒ Sử dụng định lí: Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) song song với nhau. Nếu \(\left( R \right)\) cắt \(\left( P \right)\) thì cắt \(\left( Q \right)\) và hai giao tuyến của chúng song song.
Lời giải chi tiết:
Ta có:
\(\left. \begin{array}{l}\left( Q \right)\parallel \left( R \right)\\\left( P \right) \cap \left( Q \right) = a'\\\left( P \right) \cap \left( R \right) = b'\end{array} \right\} \Rightarrow a'\parallel b'\)
Vậy nếu \(\left( Q \right)\parallel \left( R \right)\) thì \(a'\parallel b'\); nếu \(\left( Q \right) \equiv \left( R \right)\) thì \(a' \equiv b'\).
Thực hành 2
Cho hình thang \(ABCD\) có đáy lớn \(AB\) và \(AB = 2CD\), hình chiếu song song của \(ABCD\) là tứ giác \(A'B'C'D'\). Chứng minh rằng \(A'B'C'D'\) cũng là một hình thang và \(A'B' = 2C'D'\).
Phương pháp giải:
Sử dụng tính chất của phép chiếu song song:
‒ Hình chiếu song song của hai đường thẳng song song là hai đường thẳng song song hoặc trùng nhau.
‒ Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau.
Lời giải chi tiết:
\(ABCD\) là hình thang có đáy lớn \(AB \Rightarrow AB\parallel CD\).
Vì hình chiếu song song của hai đường thẳng song song là hai đường thẳng song song hoặc trùng nhau, mà hình chiếu song song của \(ABCD\) là tứ giác \(A'B'C'D'\) nên \(A'B'\parallel C'D'\). Vậy \(A'B'C'D'\) cũng là một hình thang.
Vì phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau, mà \(AB = 2CD,AB\parallel CD\) và \(A'B'\parallel C'D'\) nên \(A'B' = 2C'D'\).
Vận dụng 2
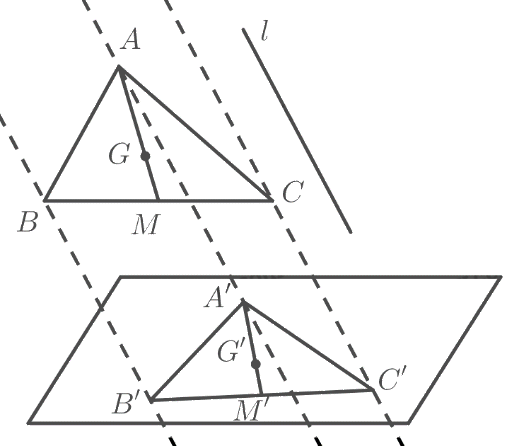
Cho \(G\) là trọng tâm tam giác \(ABC\), \(M\) là trung điểm \(BC\) và hình chiếu song song của tam giác \(ABC\) là tam giác \(A'B'C'\). Chứng minh rằng hình chiếu \(M'\) của \(M\) là trung điểm của \(B'C'\) và hình chiếu \(G'\) của \(G\) cũng là trọng tâm tam giác \(A'B'C'\).
Phương pháp giải:
Sử dụng tính chất của phép chiếu song song:
‒ Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.
‒ Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau.
Lời giải chi tiết:

Vì phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó nên có \(M\) nằm giữa \(B\) và \(C\) thì \(M'\) nằm giữa \(B'\) và \(C'\).
Vì phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau nên có \(MB = MC\) thì \(M'B' = M'C'\).
Vậy \(M'\) là trung điểm của \(B'C'\).
Vì phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó nên có \(G\) nằm giữa \(A\) và \(M\) thì \(G'\) nằm giữa \(A'\) và \(M'\).
Vì phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau nên có \(AG = \frac{2}{3}AM\) thì \(A'G' = \frac{2}{3}A'M'\).
Vậy \(G'\) là trọng tâm tam giác \(A'B'C'\).
Giải mục 2 trang 122, 123, 124 SGK Toán 11 tập 1 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 2 của SGK Toán 11 tập 1 Chân trời sáng tạo tập trung vào các kiến thức về phép biến hình. Đây là một phần quan trọng trong chương trình học, giúp học sinh hiểu rõ hơn về các khái niệm cơ bản như phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc nắm vững các kiến thức này không chỉ giúp các em giải quyết các bài tập trong SGK mà còn là nền tảng cho các kiến thức nâng cao hơn trong các lớp học tiếp theo.
Nội dung chính của Mục 2
- Phép tịnh tiến: Định nghĩa, tính chất và ứng dụng của phép tịnh tiến trong hình học.
- Phép quay: Định nghĩa, tính chất và ứng dụng của phép quay trong hình học.
- Phép đối xứng trục: Định nghĩa, tính chất và ứng dụng của phép đối xứng trục trong hình học.
- Phép đối xứng tâm: Định nghĩa, tính chất và ứng dụng của phép đối xứng tâm trong hình học.
Giải chi tiết các bài tập trang 122, 123, 124
Dưới đây là lời giải chi tiết cho từng bài tập trong Mục 2, trang 122, 123, 124 SGK Toán 11 tập 1 Chân trời sáng tạo:
Bài 1 (Trang 122)
Đề bài: Cho điểm A(1; 2). Tìm tọa độ điểm A' là ảnh của A qua phép tịnh tiến theo vectơ v = (3; -1).
Lời giải:
Sử dụng công thức phép tịnh tiến: x' = x + vx, y' = y + vy
Trong đó: A'(x'; y') là ảnh của A(x; y) qua phép tịnh tiến theo vectơ v = (vx; vy)
Áp dụng vào bài toán, ta có:
x' = 1 + 3 = 4
y' = 2 + (-1) = 1
Vậy A'(4; 1).
Bài 2 (Trang 123)
Đề bài: Cho đường thẳng d: x + 2y - 3 = 0. Tìm phương trình đường thẳng d' là ảnh của d qua phép quay tâm O góc 90°.
Lời giải:
(Lời giải chi tiết cho bài 2 sẽ được trình bày tại đây, bao gồm các bước thực hiện và giải thích cụ thể)
Bài 3 (Trang 124)
Đề bài: Cho đường tròn (C): (x - 1)² + (y + 2)² = 4. Tìm phương trình đường tròn (C') là ảnh của (C) qua phép đối xứng trục Ox.
Lời giải:
(Lời giải chi tiết cho bài 3 sẽ được trình bày tại đây, bao gồm các bước thực hiện và giải thích cụ thể)
Mẹo học tốt môn Toán 11
- Nắm vững định nghĩa và tính chất: Đây là nền tảng để giải quyết mọi bài tập.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng bài và rèn luyện kỹ năng.
- Sử dụng các công cụ hỗ trợ: Máy tính bỏ túi, phần mềm vẽ đồ thị,... có thể giúp bạn giải quyết các bài tập một cách nhanh chóng và chính xác.
- Hỏi thầy cô và bạn bè: Đừng ngần ngại hỏi khi gặp khó khăn.
Tusach.vn hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể này, các em sẽ học tốt môn Toán 11 và đạt kết quả cao trong các kỳ thi. Chúc các em thành công!