Giải mục 1 trang 80, 81 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 1 trang 80, 81 SGK Toán 11 tập 1 - Chân trời sáng tạo
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Toán 11 tập 1 Chân trời sáng tạo. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, vì vậy chúng tôi luôn cố gắng mang đến những giải pháp tốt nhất để giúp bạn học tập hiệu quả.
Bài viết này sẽ tập trung vào việc giải mục 1 trang 80, 81, giúp bạn hiểu rõ các khái niệm và phương pháp giải bài tập liên quan.
Cho hàm số \(y = f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}1&{khi\,\,0 \le x \le 1}\\{1 + x}&{khi\,\,1 < x \le 2}\\{5 - x}&{khi\,\,2 < x \le 3}\end{array}} \right.\) có đồ thị như Hình 1.
Hoạt động 1
Cho hàm số \(y = f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}1&{khi\,\,0 \le x \le 1}\\{1 + x}&{khi\,\,1 < x \le 2}\\{5 - x}&{khi\,\,2 < x \le 3}\end{array}} \right.\) có đồ thị như Hình 1.
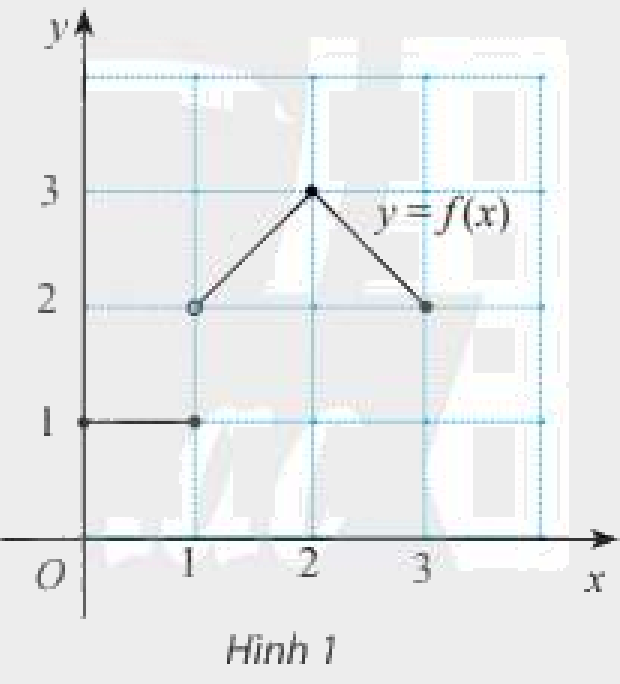
Tại mỗi điểm \({x_0} = 1\) và \({x_0} = 2\), có tồn tại giới hạn \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right)\) không? Nếu có, giới hạn đó có bằng \(f\left( {{x_0}} \right)\) không?
Phương pháp giải:
Bước 1: Tính các giới hạn một bên \(\mathop {\lim }\limits_{x \to {x_0}^ + } f\left( x \right),\mathop {\lim }\limits_{x \to {x_0}^ - } {\rm{ }}f\left( x \right)\).
Bước 2: So sánh \(\mathop {\lim }\limits_{x \to {x_0}^ + } f\left( x \right),\mathop {\lim }\limits_{x \to {x_0}^ - } {\rm{ }}f\left( x \right)\)
• Nếu \(\mathop {\lim }\limits_{x \to {x_0}^ + } f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}^ - } {\rm{ }}f\left( x \right) = L\) thì \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = L\).
• Nếu \(\mathop {\lim }\limits_{x \to {x_0}^ + } f\left( x \right) \ne \mathop {\lim }\limits_{x \to {x_0}^ - } {\rm{ }}f\left( x \right)\) thì không tồn tại \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right)\).
Lời giải chi tiết:
• \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {1 + x} \right) = 1 + 1 = 2\).
\(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} 1 = 1\).
Vì \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {1^ - }} {\rm{ }}f\left( x \right)\) nên không tồn tại \(\mathop {\lim }\limits_{x \to 1} f\left( x \right)\).
• \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( {5 - x} \right) = 5 - 2 = 3\).
\(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {1 + x} \right) = 1 + 2 = 3\).
Vì \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} {\rm{ }}f\left( x \right) = 3\) nên \(\mathop {\lim }\limits_{x \to 2} f\left( x \right) = 3\).
Ta có: \(f\left( 2 \right) = 1 + 2 = 3\).
Vậy \(\mathop {\lim }\limits_{x \to 2} f\left( x \right) = f\left( 2 \right)\).
Thực hành 1
Xét tính liên tục của hàm số:
a) \(f\left( x \right) = 1 - {x^2}\) tại điểm \({x_0} = 3\);
b) \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{{x^2} + 1}&{khi\,\,x > 1}\\{ - x}&{khi\,\,x \le 1}\end{array}} \right.\) tại điểm \({x_0} = 1\).
Phương pháp giải:
Bước 1: Kiểm tra \({x_0}\) thuộc tập xác định. Tính \(f\left( {{x_0}} \right)\).
Bước 2: Tính \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right)\) (nếu có).
Bước 3: Kết luận:
• Nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\) thì hàm số liên tục tại điểm \({x_0}\).
• Nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) \ne f\left( {{x_0}} \right)\) hoặc không tồn tại \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right)\) thì hàm số không liên tục tại điểm \({x_0}\).
Lời giải chi tiết:
a) \(f\left( 3 \right) = 1 - {3^2} = 1 - 9 = - 8\).
\(\mathop {\lim }\limits_{x \to 3} f\left( x \right) = \mathop {\lim }\limits_{x \to 3} \left( {1 - {x^2}} \right) = 1 - {3^2} = 1 - 9 = - 8\).
Vì \(\mathop {\lim }\limits_{x \to 3} f\left( x \right) = f\left( 3 \right) = - 8\) nên hàm số \(y = f\left( x \right)\) liên tục tại điểm \({x_0} = 3\).
b) \(f\left( 1 \right) = - 1\).
\(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {{x^2} + 1} \right) = {1^2} + 1 = 2\).
\(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \left( { - x} \right) = - 1\).
Vì \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {1^ - }} {\rm{ }}f\left( x \right)\) nên không tồn tại \(\mathop {\lim }\limits_{x \to 1} f\left( x \right)\)
Vậy hàm số không liên tục tại điểm \({x_0} = 1\).
Giải mục 1 trang 80, 81 SGK Toán 11 tập 1 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu
Mục 1 của chương trình Toán 11 tập 1 Chân trời sáng tạo thường xoay quanh các khái niệm cơ bản về hàm số, bao gồm định nghĩa, các loại hàm số, tập xác định, tập giá trị, và cách biểu diễn hàm số. Việc nắm vững những kiến thức này là nền tảng quan trọng để giải quyết các bài tập phức tạp hơn trong chương trình học.
Nội dung chính của Mục 1 trang 80, 81
Thông thường, mục này sẽ bao gồm các bài tập sau:
- Xác định tập xác định của hàm số.
- Tìm tập giá trị của hàm số.
- Kiểm tra tính chẵn, lẻ của hàm số.
- Vẽ đồ thị hàm số.
- Giải các bài toán ứng dụng liên quan đến hàm số.
Hướng dẫn giải chi tiết các bài tập
Để giúp bạn hiểu rõ hơn, chúng ta sẽ đi vào giải chi tiết một số bài tập tiêu biểu trong mục 1 trang 80, 81:
Bài 1: Xác định tập xác định của hàm số y = √(2x - 1)
Để hàm số y = √(2x - 1) xác định, điều kiện cần và đủ là 2x - 1 ≥ 0. Giải bất phương trình này, ta được x ≥ 1/2. Vậy tập xác định của hàm số là D = [1/2, +∞).
Bài 2: Tìm tập giá trị của hàm số y = x2 - 4x + 3
Hàm số y = x2 - 4x + 3 là một hàm bậc hai có hệ số a = 1 > 0, do đó hàm số có giá trị nhỏ nhất tại đỉnh của parabol. Hoành độ đỉnh là x = -b/2a = -(-4)/(2*1) = 2. Giá trị nhỏ nhất của hàm số là y = 22 - 4*2 + 3 = -1. Vậy tập giá trị của hàm số là [ -1, +∞).
Bài 3: Kiểm tra tính chẵn, lẻ của hàm số y = x3 + 2x
Để kiểm tra tính chẵn, lẻ của hàm số, ta cần xét f(-x). Ta có f(-x) = (-x)3 + 2(-x) = -x3 - 2x = -(x3 + 2x) = -f(x). Vì f(-x) = -f(x) với mọi x thuộc tập xác định, nên hàm số y = x3 + 2x là hàm số lẻ.
Mẹo giải nhanh các bài tập về hàm số
Để giải nhanh các bài tập về hàm số, bạn có thể áp dụng một số mẹo sau:
- Nắm vững định nghĩa và các tính chất cơ bản của hàm số.
- Sử dụng các công thức và phương pháp giải toán đã học.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng máy tính bỏ túi để kiểm tra lại kết quả.
Tại sao nên chọn tusach.vn để học Toán 11?
tusach.vn tự hào là một trong những trang web hàng đầu cung cấp lời giải bài tập Toán 11 chính xác và dễ hiểu. Chúng tôi có đội ngũ giáo viên giàu kinh nghiệm, luôn cập nhật kiến thức mới nhất và phương pháp giảng dạy hiệu quả. Ngoài ra, chúng tôi còn cung cấp nhiều tài liệu học tập hữu ích khác, như lý thuyết, bài tập trắc nghiệm, và đề thi thử.
Hãy truy cập tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích và nâng cao kết quả học tập của bạn!
| Chương | Bài | Nội dung |
|---|---|---|
| 1 | 1 | Hàm số và đồ thị |
| 1 | 2 | Hàm số bậc hai |