Lý thuyết Hai đường thẳng song song - SGK Toán 11 Chân trời sáng tạo
Tổng quan nội dung
Lý thuyết Hai đường thẳng song song - Toán 11 Chân trời sáng tạo
Bài học này cung cấp kiến thức nền tảng về hai đường thẳng song song, một trong những khái niệm quan trọng trong hình học không gian.
Chúng ta sẽ cùng tìm hiểu các điều kiện để hai đường thẳng song song, các tính chất liên quan đến góc so le trong, góc đồng vị và góc trong cùng phía.
Nội dung được trình bày chi tiết, dễ hiểu, giúp học sinh nắm vững lý thuyết và áp dụng vào giải bài tập một cách hiệu quả.
1. Vị trí tương đối của hai đường thẳng
1. Vị trí tương đối của hai đường thẳng
Cho hai đường thẳng a, b trong không gian.
- Nếu a và b cùng nằm trong một mặt phẳng thì ta nói a và b đồng phẳng. Khi đó, a và b có thể cắt nhau, song song với nhau hoặc trùng nhau.
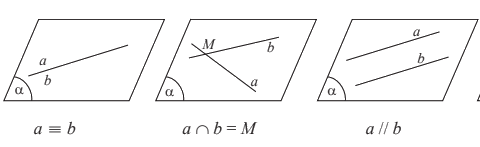
- Nếu a và b không cùng nằm trong bất kì mặt phẳng nào thì ta nói a và b chéo nhau. Khi đó, ta cũng nói a chéo với b hoặc b chéo với a.
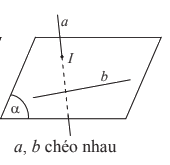
* Hai đường thẳng song song là hai đường thẳng cùng nằm trong một mặt phẳng và không có điểm chung. Kí hiệu //.
* Chú ý:
- Hai đường thẳng gọi là chéo nhau nếu chúng không đồng phẳng (tức là không cùng nằm trong một mặt phẳng).
- Có duy nhất một mặt phẳng chứa 2 đường thẳng song song (a // b), kí hiệu mp(a,b).
2. Tính chất cơ bản của hai đường thẳng song song
- Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có đúng một đường thẳng song song với đường thẳng đã cho.
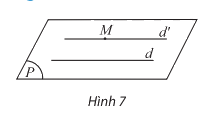
- Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì 3 giao tuyến đó đồng quy hoặc đôi một song song.
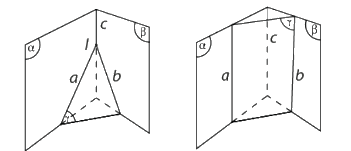
* Hệ quả: Nếu hai mặt phẳng phân biệt chứa 2 đường thẳng song song với nhau thì giao tuyến (nếu có) của chúng song song với 2 đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.

- Trong không gian, hai đường thẳng phân biệt cùng song song với đường thẳng thứ 3 thì song song với nhau.

Lý Thuyết Hai Đường Thẳng Song Song - SGK Toán 11 Chân Trời Sáng Tạo
Trong chương trình Toán 11, phần hình học không gian đóng vai trò quan trọng trong việc phát triển tư duy logic và khả năng không gian của học sinh. Một trong những khái niệm cơ bản và nền tảng nhất là lý thuyết về hai đường thẳng song song. Bài viết này sẽ cung cấp một cách đầy đủ và chi tiết về lý thuyết này, dựa trên nội dung sách giáo khoa Toán 11 Chân Trời Sáng Tạo.
1. Khái Niệm Hai Đường Thẳng Song Song
Hai đường thẳng được gọi là song song khi chúng không có điểm chung. Ký hiệu: a // b. Để xác định hai đường thẳng song song, chúng ta cần dựa vào các điều kiện sau:
- Điều kiện 1: Nếu hai đường thẳng phân biệt không có điểm chung thì chúng song song.
- Điều kiện 2: Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song.
- Điều kiện 3: Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song.
2. Các Tính Chất Quan Trọng Của Hai Đường Thẳng Song Song
Khi hai đường thẳng song song, chúng tạo ra mối quan hệ đặc biệt với các đường thẳng cắt ngang. Các tính chất quan trọng cần nắm vững bao gồm:
- Góc So Le Trong: Nếu hai đường thẳng song song cắt một đường thẳng thứ ba thì các cặp góc so le trong bằng nhau.
- Góc Đồng Vị: Nếu hai đường thẳng song song cắt một đường thẳng thứ ba thì các cặp góc đồng vị bằng nhau.
- Góc Trong Cùng Phía: Nếu hai đường thẳng song song cắt một đường thẳng thứ ba thì các cặp góc trong cùng phía bù nhau (tổng bằng 180 độ).
3. Điều Kiện Nhận Biết Hai Đường Thẳng Song Song
Ngược lại với các tính chất trên, chúng ta có thể sử dụng chúng để nhận biết hai đường thẳng song song:
- Nếu hai đường thẳng phân biệt có một cặp góc so le trong bằng nhau thì chúng song song.
- Nếu hai đường thẳng phân biệt có một cặp góc đồng vị bằng nhau thì chúng song song.
- Nếu hai đường thẳng phân biệt có một cặp góc trong cùng phía bù nhau thì chúng song song.
4. Ví Dụ Minh Họa
Ví dụ 1: Cho hình vẽ, biết góc A1 = 60 độ. Chứng minh rằng đường thẳng a song song với đường thẳng b.
Giải: Vì góc A1 và góc B1 là hai góc so le trong và góc A1 = góc B1 = 60 độ, nên đường thẳng a song song với đường thẳng b (theo dấu hiệu nhận biết hai đường thẳng song song).
5. Bài Tập Vận Dụng
Để củng cố kiến thức, hãy giải các bài tập sau:
- Cho hai đường thẳng a và b song song, bị cắt bởi đường thẳng c. Tính số đo các góc còn lại trong hình vẽ nếu biết một góc bằng 70 độ.
- Chứng minh rằng hai đường thẳng sau song song: d: y = 2x + 1 và e: y = 2x - 3.
6. Lời Khuyên Khi Học Lý Thuyết Hai Đường Thẳng Song Song
- Nắm vững định nghĩa: Hiểu rõ khái niệm hai đường thẳng song song là bước đầu tiên để tiếp cận lý thuyết.
- Phân biệt các loại góc: Góc so le trong, góc đồng vị, góc trong cùng phía là những khái niệm quan trọng, cần phân biệt rõ ràng.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau sẽ giúp bạn nắm vững kiến thức và rèn luyện kỹ năng giải toán.
- Vẽ hình minh họa: Vẽ hình minh họa sẽ giúp bạn hình dung rõ hơn về các khái niệm và tính chất.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về lý thuyết hai đường thẳng song song trong chương trình Toán 11 Chân Trời Sáng Tạo. Chúc bạn học tập tốt!