Bài 3 trang 64 Toán 11 Tập 2 - Chân trời sáng tạo

Bài 3 trang 64 SGK Toán 11 tập 2 – Chân trời sáng tạo

Bài 3 trang 64 SGK Toán 11 Tập 2 – Chân trời sáng tạo

Bài 3 trang 64 SGK Toán 11 Tập 2 thuộc chương trình học Toán 11, tập trung vào việc ôn tập chương 3: Hàm số lượng giác. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số lượng giác, các phép biến đổi lượng giác và giải phương trình lượng giác để giải quyết các bài toán cụ thể.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.

Cho hình chóp (S.ABCD) có đáy là hình vuông cạnh bằng (asqrt 2 ), có các cạnh bên đều bằng (2a).

Đề bài

Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh bằng \(a\sqrt 2 \), có các cạnh bên đều bằng \(2a\).

a) Tính góc giữa \(SC\) và \(AB\).

b) Tính diện tích hình chiếu vuông góc của tam giác \(SAB\) trên mặt phẳng \(\left( {ABCD} \right)\).

Phương pháp giải - Xem chi tiết Bài 3 trang 64 SGK Toán 11 tập 2 – Chân trời sáng tạo 1

a) Cách xác định góc giữa hai đường thẳng \(a\) và \(b\):

Bước 1: Lấy một điểm \(O\) bất kì.

Bước 2: Qua điểm \(O\) dựng đường thẳng \(a'\parallel a\) và đường thẳng \(b'\parallel b\).

Bước 3: Tính \(\left( {a,b} \right) = \left( {a',b'} \right)\).

b) Sử dụng phép chiếu vuông góc.

Lời giải chi tiết

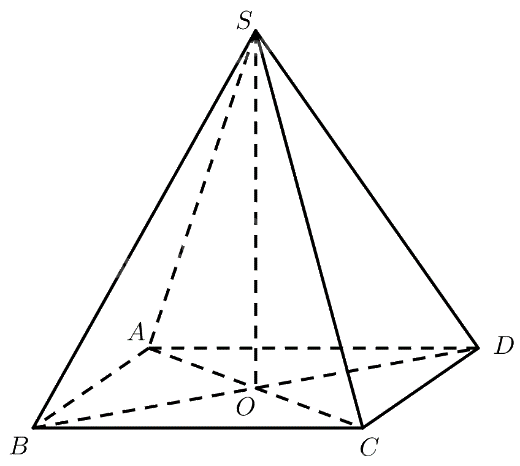
Bài 3 trang 64 SGK Toán 11 tập 2 – Chân trời sáng tạo 2

a) Ta có:

\(AB\parallel C{\rm{D}} \Rightarrow \left( {SC,AB} \right) = \left( {SC,C{\rm{D}}} \right) = \widehat {SC{\rm{D}}}\)

Xét \(\Delta SCD\) có:

\(\cos \widehat {SCD} = \frac{{S{C^2} + C{{\rm{D}}^2} - S{{\rm{D}}^2}}}{{2.SC.C{\rm{D}}}} = \frac{{\sqrt 2 }}{4} \Rightarrow \widehat {SCD} \approx {69^ \circ }18'\)

Vậy \(\left( {SC,AB} \right) \approx {69^ \circ }18'\).

b) Gọi \(O = AC \cap B{\rm{D}}\).

\(\Delta SAC\) cân tại \(S \Rightarrow SO \bot AC\)

\(\Delta SB{\rm{D}}\) cân tại \(S \Rightarrow SO \bot B{\rm{D}}\)

\( \Rightarrow SO \bot \left( {ABCD} \right) \Rightarrow O\) là hình chiếu vuông góc của \(S\) lên mặt phẳng \(\left( {ABCD} \right)\).

Lại có \(A,B \in \left( {ABCD} \right)\).

Vậy tam giác \(OAB\) là hình chiếu vuông góc của tam giác \(SAB\) lên mặt phẳng \(\left( {ABCD} \right)\)

Ta có: \(AC = \sqrt {A{B^2} + B{C^2}} = 2a\)

Mà ABCD là hình vuông nên O là trung điểm của mỗi đường chéo.

\(\begin{array}{l} \Rightarrow AO = BO = \frac{{AC}}{2} = a\\ \Rightarrow {S_{OAB}} = \frac{1}{2}AO.BO = \frac{1}{2}a.a = \frac{1}{2}{a^2}\end{array}\)

Vậy diện tích hình chiếu vuông góc của tam giác SAB trên mặt phẳng (ABCD) là \(\frac{1}{2}{a^2}\)

Bài 3 trang 64 SGK Toán 11 Tập 2 – Chân trời sáng tạo: Giải chi tiết và hướng dẫn

Bài 3 trang 64 SGK Toán 11 Tập 2 Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Hàm số lượng giác. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về hàm số lượng giác, bao gồm:

Định nghĩa các hàm số lượng giác (sin, cos, tan, cot)
Tập xác định và tập giá trị của các hàm số lượng giác
Tính chất tuần hoàn của các hàm số lượng giác
Các công thức lượng giác cơ bản (công thức cộng, trừ, nhân đôi, chia đôi)
Phương pháp giải phương trình lượng giác

Dưới đây là nội dung chi tiết của bài tập và lời giải:

Nội dung bài tập:

(Giả sử nội dung bài tập là: Giải các phương trình lượng giác sau: a) sin(x) = 1/2; b) cos(x) = -√3/2; c) tan(x) = 1)

Lời giải:

a) Giải phương trình sin(x) = 1/2

Phương trình sin(x) = 1/2 có nghiệm là:

x = π/6 + k2π (k ∈ Z)
x = 5π/6 + k2π (k ∈ Z)

b) Giải phương trình cos(x) = -√3/2

Phương trình cos(x) = -√3/2 có nghiệm là:

x = 5π/6 + k2π (k ∈ Z)
x = 7π/6 + k2π (k ∈ Z)

c) Giải phương trình tan(x) = 1

Phương trình tan(x) = 1 có nghiệm là:

x = π/4 + kπ (k ∈ Z)

Mở rộng và bài tập tương tự

Để củng cố kiến thức về hàm số lượng giác và phương pháp giải phương trình lượng giác, học sinh có thể tự giải các bài tập tương tự sau:

Giải phương trình sin(2x) = √2/2
Giải phương trình cos(x/2) = 0
Giải phương trình tan(3x) = √3

Ngoài ra, học sinh nên tham khảo thêm các tài liệu học tập khác, như sách bài tập, đề thi thử, và các trang web học trực tuyến để nâng cao kiến thức và kỹ năng giải toán.

Lưu ý khi giải bài tập về hàm số lượng giác

Khi giải các bài tập về hàm số lượng giác, học sinh cần lưu ý những điều sau:

Xác định đúng tập xác định của hàm số lượng giác.
Sử dụng đúng các công thức lượng giác.
Kiểm tra lại kết quả để đảm bảo tính chính xác.
Luyện tập thường xuyên để nắm vững kiến thức và kỹ năng.

tusach.vn hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh sẽ hiểu rõ hơn về Bài 3 trang 64 SGK Toán 11 Tập 2 – Chân trời sáng tạo và tự tin giải các bài tập tương tự. Chúc các em học tốt!