Bài 12 Trang 128 Toán 11 Tập 1 - Chân Trời Sáng Tạo

Bài 12 trang 128 SGK Toán 11 tập 1 - Chân trời sáng tạo

Bài 12 thuộc chương trình học Toán 11 tập 1, tập trung vào việc ôn tập chương 3: Hàm số lượng giác. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số lượng giác, các phép biến đổi lượng giác và giải phương trình lượng giác để giải quyết các bài toán cụ thể.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.

Cho hai hình bình hành (ABCD) và (ABEF) nằm trong hai mặt phẳng khác nhau. Lấy các điểm (M,N) lần lượt thuộc các đường chéo (AC) và (BF) sao cho (MC = 2MA;NF = 2NB). Qua (M,N) kẻ các đường thẳng song song với (AB), cắt các cạnh (AD,AF) lần lượt tại ({M_1},{N_1}). Chứng minh rằng:

Đề bài

Cho hai hình bình hành \(ABCD\) và \(ABEF\) nằm trong hai mặt phẳng khác nhau. Lấy các điểm \(M,N\) lần lượt thuộc các đường chéo \(AC\) và \(BF\) sao cho \(MC = 2MA;NF = 2NB\). Qua \(M,N\) kẻ các đường thẳng song song với \(AB\), cắt các cạnh \(AD,AF\) lần lượt tại \({M_1},{N_1}\). Chứng minh rằng:

a) \(MN\parallel DE\);

b) \({M_1}{N_1}\parallel \left( {DEF} \right)\);

c) \(\left( {MN{N_1}{M_1}} \right)\parallel \left( {DEF} \right)\).

Phương pháp giải - Xem chi tiết Bài 12 trang 128 SGK Toán 11 tập 1 - Chân trời sáng tạo 1

Sử dụng các định lí, tính chất:

‒ Tính chất trọng tâm của tam giác.

‒ Định lí Thalès trong tam giác.

– Nếu đường thẳng \(a\) không nằm trong mặt phẳng \(\left( P \right)\) và song song với một đường thẳng \(b\) nào đó nằm trong \(\left( P \right)\) thì \(a\) song song với \(\left( P \right)\).

‒ Nếu mặt phẳng \(\left( P \right)\) chứa hai đường thẳng \(a,b\) cắt nhau và hai đường thẳng đó cùng song song với mặt phẳng \(\left( Q \right)\) thì \(\left( P \right)\) song song với \(\left( Q \right)\).

Lời giải chi tiết

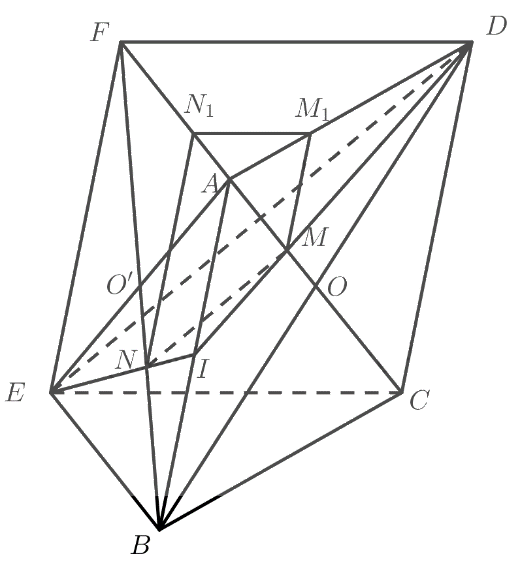
Bài 12 trang 128 SGK Toán 11 tập 1 - Chân trời sáng tạo 2

a) Vì AI // CD nên \(\frac{{AI}}{{CD}} = \frac{{IM}}{{MD}} = \frac{{AM}}{{MC}} = \frac{1}{2}\) (định lý Thales).

Vì IB // EF nên \(\frac{{IB}}{{EF}} = \frac{{IN}}{{NE}} = \frac{{BN}}{{NF}} = \frac{1}{2}\) (định lý Thales).

Do đó \(\frac{{IM}}{{MD}} = \frac{{IN}}{{NE}} = \frac{1}{2}\), suy ra MN // DE (định lý Thales đảo).

b) Theo giả thiết, AB // \(M{M_1}\) và \(M{M_1}\) không thuộc (ABEF) nên \(M{M_1}\) // (ABEF).

c) Ta có \(M{M_1}\) // AB // EF, suy ra \(M{M_1}\) // (DEF) (1)

Vì \(N{N_1}\) // AB nên \(\frac{{A{N_1}}}{{{N_1}F}} = \frac{{BN}}{{NF}} = \frac{1}{2}\) (định lý Thales).

Vì \(M{M_1}\) // AB nên \(\frac{{A{M_1}}}{{{M_1}D}} = \frac{{AM}}{{MC}} = \frac{1}{2}\) (định lý Thales).

Do đó \(\frac{{A{N_1}}}{{{N_1}F}} = \frac{{A{M_1}}}{{{M_1}D}} = \frac{1}{2}\), suy ra \({M_1}{N_1}\) // DF và \({M_1}{N_1}\) // (DEF) (2).

Mà \(M{M_1}\) cắt \({M_1}{N_1}\) (3).

Từ (1), (2), (3) suy ra \((MN{N_1}{M_1})\) // (DEF).

Bài 12 Trang 128 SGK Toán 11 Tập 1 - Chân Trời Sáng Tạo: Giải Chi Tiết & Đầy Đủ

Chào mừng các em học sinh đến với lời giải chi tiết Bài 12 trang 128 SGK Toán 11 tập 1 - Chân trời sáng tạo. Bài tập này là một phần quan trọng trong quá trình ôn tập chương 3 về Hàm số lượng giác, giúp các em củng cố kiến thức và rèn luyện kỹ năng giải toán.

Nội Dung Chính của Bài 12

Bài 12 thường bao gồm các dạng bài tập sau:

Xác định tập xác định của hàm số lượng giác: Yêu cầu học sinh xác định khoảng giá trị của x để hàm số có nghĩa.
Tìm tập giá trị của hàm số lượng giác: Xác định khoảng giá trị mà hàm số có thể đạt được.
Khảo sát sự biến thiên của hàm số lượng giác: Tìm khoảng đồng biến, nghịch biến, cực trị của hàm số.
Giải phương trình lượng giác: Sử dụng các công thức lượng giác và phương pháp giải phương trình để tìm nghiệm.
Ứng dụng hàm số lượng giác vào giải quyết bài toán thực tế: Áp dụng kiến thức về hàm số lượng giác để mô tả và giải quyết các bài toán liên quan đến vật lý, kỹ thuật,...

Lời Giải Chi Tiết Bài 12 (Ví dụ)

Để minh họa, chúng ta sẽ xem xét một ví dụ cụ thể. Giả sử bài tập yêu cầu:

"Tìm tập xác định của hàm số y = tan(2x - π/3)"

Lời giải:

Hàm số y = tan(u) xác định khi và chỉ khi u ≠ π/2 + kπ, với k là số nguyên. Do đó, để hàm số y = tan(2x - π/3) xác định, ta cần:

2x - π/3 ≠ π/2 + kπ

2x ≠ 5π/6 + kπ

x ≠ 5π/12 + kπ/2, với k là số nguyên.

Vậy, tập xác định của hàm số là D = R \ {5π/12 + kπ/2 | k ∈ Z}.

Mẹo Giải Toán Lượng Giác Hiệu Quả

Để giải các bài tập về hàm số lượng giác một cách hiệu quả, các em nên:

Nắm vững các công thức lượng giác cơ bản: Công thức cộng, trừ, nhân đôi, chia đôi, hạ bậc,...
Biết cách biến đổi lượng giác: Sử dụng các công thức để đưa phương trình về dạng đơn giản hơn.
Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng bài và rèn luyện kỹ năng.
Sử dụng máy tính bỏ túi: Kiểm tra lại kết quả và tính toán các giá trị lượng giác phức tạp.

Tài Liệu Tham Khảo Hữu Ích

Ngoài SGK Toán 11 tập 1 - Chân trời sáng tạo, các em có thể tham khảo thêm các tài liệu sau:

Sách bài tập Toán 11
Các trang web học Toán trực tuyến uy tín (ví dụ: tusach.vn)
Các video bài giảng trên YouTube

Kết Luận

Bài 12 trang 128 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp các em củng cố kiến thức về hàm số lượng giác. Hy vọng với lời giải chi tiết và các mẹo giải toán hiệu quả mà tusach.vn cung cấp, các em sẽ học tập tốt và đạt kết quả cao trong môn Toán.

Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với chúng tôi để được hỗ trợ!

Bài 12 trang 128 SGK Toán 11 tập 1 - Chân trời sáng tạo

Bài 12 trang 128 SGK Toán 11 tập 1 - Chân trời sáng tạo

Bài 12 Trang 128 SGK Toán 11 Tập 1 - Chân Trời Sáng Tạo: Giải Chi Tiết & Đầy Đủ

Nội Dung Chính của Bài 12

Lời Giải Chi Tiết Bài 12 (Ví dụ)

Mẹo Giải Toán Lượng Giác Hiệu Quả

Tài Liệu Tham Khảo Hữu Ích

Kết Luận

CHỦ ĐỀ SÁCH XEM NHIỀU

VỀ TUSACH.VN