Bài 2 trang 112 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Bài 2 trang 112 SGK Toán 11 Tập 1 - Chân trời sáng tạo
Bài 2 thuộc chương trình học Toán 11 Tập 1, sách Chân trời sáng tạo, tập trung vào việc rèn luyện kỹ năng giải quyết các bài toán liên quan đến giới hạn của hàm số. Bài tập này giúp học sinh củng cố kiến thức đã học và chuẩn bị cho các bài học tiếp theo.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững phương pháp giải và tự tin làm bài tập.
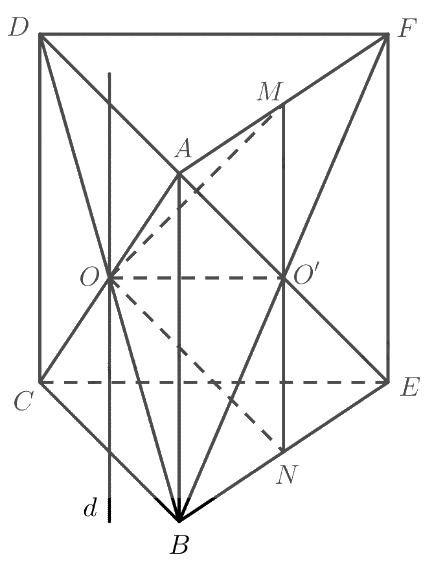
Cho hai hình bình hành \(ABCD\) và \(ABEF\) không nằm trong cùng một mặt phẳng. Gọi \(O\) và \(O'\) lần lượt là tâm của \(ABCD\) và \(ABEF\).
Đề bài
Cho hai hình bình hành \(ABCD\) và \(ABEF\) không nằm trong cùng một mặt phẳng. Gọi \(O\) và \(O'\) lần lượt là tâm của \(ABCD\) và \(ABEF\).
a) Chứng minh đường thẳng \(OO'\) song song với các mặt phẳng \(\left( {CDF{\rm{E}}} \right),\left( {ADF} \right)\) và \(\left( {BCE} \right)\).
b) Gọi \(M\) và \(N\) lần lượt là trung điểm của \(AF\) và \(BE\). Chứng minh \(MN\parallel \left( {CDF{\rm{E}}} \right)\).
c) Tìm giao tuyến của hai mặt phẳng \(\left( {OMN} \right)\) và \(\left( {ABCD} \right)\).
Phương pháp giải - Xem chi tiết
– Để chứng minh đường thẳng song song với mặt phẳng, ta chứng minh đường thẳng đấy không nằm trong mặt phẳng và song song với một đường thẳng nằm trong mặt phẳng.
‒ Để tìm giao tuyến của hai mặt phẳng, ta có 2 cách:
+ Cách 1: Tìm 2 điểm chung phân biệt. Giao tuyến là đường thẳng đi qua hai điểm chung.
+ Cách 2: Tìm 1 điểm chung và 2 đường thẳng song song nằm trên mỗi mặt phẳng. Giao tuyến là đường thẳng đi qua điểm chung và song song với hai đường thẳng đó.
Lời giải chi tiết
a) \(O\) là trung điểm của \(B{\rm{D}}\) (theo tính chất hình bình hành)
\(O'\) là trung điểm của \(BF\) (theo tính chất hình bình hành)
\( \Rightarrow OO'\) là đường trung bình của tam giác \(B{\rm{D}}F\)
\(\left. \begin{array}{l} \Rightarrow OO'\parallel DF\\DF \subset \left( {C{\rm{DFE}}} \right)\end{array} \right\} \Rightarrow OO'\parallel \left( {C{\rm{DFE}}} \right)\)
Ta có:
\(\left. \begin{array}{l}OO'\parallel DF\\DF \subset \left( {A{\rm{DF}}} \right)\end{array} \right\} \Rightarrow OO'\parallel \left( {A{\rm{DF}}} \right)\)
\(O\) là trung điểm của \(AC\) (theo tính chất hình bình hành)
\(O'\) là trung điểm của \(A{\rm{E}}\) (theo tính chất hình bình hành)
\( \Rightarrow OO'\) là đường trung bình của tam giác \(AC{\rm{E}}\)
\(\left. \begin{array}{l} \Rightarrow OO'\parallel CE\\CE \subset \left( {BCE} \right)\end{array} \right\} \Rightarrow OO'\parallel \left( {BC{\rm{E}}} \right)\)
b) \(M\) là trung điểm của \(AF\) (theo tính chất hình bình hành)
\(N\) là trung điểm của \(BE\) (theo tính chất hình bình hành)
\( \Rightarrow MN\) là đường trung bình của hình bình hành \(ABEF\)
\(\left. \begin{array}{l} \Rightarrow MN\parallel EF\parallel AB\\EF \subset \left( {C{\rm{D}}F{\rm{E}}} \right)\end{array} \right\} \Rightarrow MN\parallel \left( {C{\rm{D}}F{\rm{E}}} \right)\)
Ta có:
\(\left. \begin{array}{l}O \in \left( {OMN} \right) \cap \left( {ABC{\rm{D}}} \right)\\MN\parallel AB\\MN \subset \left( {OMN} \right)\\AB \subset \left( {ABC{\rm{D}}} \right)\end{array} \right\}\)
\( \Rightarrow \)Giao tuyến của hai mặt phẳng \(\left( {OMN} \right)\) và \(\left( {ABCD} \right)\) là đường thẳng \(d\) đi qua \(O\), song song với \(MN\) và \(AB\).
Bài 2 trang 112 SGK Toán 11 Tập 1 - Chân trời sáng tạo: Giải chi tiết và hướng dẫn
Bài 2 trang 112 SGK Toán 11 Tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học về giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức về giới hạn một bên, giới hạn tại một điểm và các tính chất của giới hạn để giải quyết các bài toán cụ thể.
Nội dung bài tập
Bài 2 thường bao gồm các dạng bài tập sau:
- Tính giới hạn của hàm số tại một điểm cho trước.
- Xác định xem một hàm số có giới hạn tại một điểm hay không.
- Sử dụng định nghĩa giới hạn để chứng minh một khẳng định.
Phương pháp giải
Để giải quyết bài tập này, học sinh cần nắm vững các kiến thức sau:
- Định nghĩa giới hạn: Hiểu rõ định nghĩa giới hạn của hàm số tại một điểm.
- Giới hạn một bên: Biết cách tính giới hạn bên trái và giới hạn bên phải của hàm số.
- Các tính chất của giới hạn: Vận dụng các tính chất của giới hạn để đơn giản hóa bài toán.
- Các dạng giới hạn đặc biệt: Nhận biết và sử dụng các dạng giới hạn đặc biệt như giới hạn của sinx/x, (1+x)^n/x,...
Lời giải chi tiết Bài 2 trang 112 SGK Toán 11 Tập 1 - Chân trời sáng tạo
(Ở đây sẽ là lời giải chi tiết cho từng câu của bài 2. Ví dụ:)
Câu a: Tính limx→2 (x2 - 4) / (x - 2)
Lời giải:
(x2 - 4) / (x - 2) = (x - 2)(x + 2) / (x - 2) = x + 2 (với x ≠ 2)
limx→2 (x2 - 4) / (x - 2) = limx→2 (x + 2) = 2 + 2 = 4
Bài tập tương tự
Để củng cố kiến thức, các em có thể làm thêm các bài tập tương tự sau:
- Tính limx→1 (x3 - 1) / (x - 1)
- Tính limx→0 sin(x) / x
Lưu ý khi giải bài tập về giới hạn
Khi giải bài tập về giới hạn, các em cần chú ý:
- Kiểm tra xem hàm số có xác định tại điểm cần tính giới hạn hay không.
- Sử dụng các phương pháp đại số để đơn giản hóa biểu thức.
- Áp dụng các định lý và tính chất của giới hạn một cách chính xác.
Hy vọng với lời giải chi tiết và hướng dẫn này, các em học sinh sẽ hiểu rõ hơn về Bài 2 trang 112 SGK Toán 11 Tập 1 - Chân trời sáng tạo và tự tin hơn trong quá trình học tập. Hãy truy cập tusach.vn để xem thêm nhiều bài giải và tài liệu học tập hữu ích khác.