Bài 4 trang 112 Toán 11 Tập 1 - Chân trời sáng tạo

Bài 4 trang 112 SGK Toán 11 tập 1 - Chân trời sáng tạo

Bài 4 trang 112 SGK Toán 11 Tập 1 - Chân trời sáng tạo

Bài 4 thuộc chương trình học Toán 11 Tập 1, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến phép biến hóa lượng giác. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để tìm nghiệm của phương trình lượng giác.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

Cho tứ diện (ABCD) và điểm (M) thuộc cạnh (AB). Gọi (left( alpha right)) là mặt phẳng qua (M), song song với hai đường thẳng (BC) và (AD). Gọi (N,P,Q) lần lượt là giao điểm của mặt phẳng (left( alpha right)) với các cạnh (AC,CD) và (DB).

Đề bài

Cho tứ diện \(ABCD\) và điểm \(M\) thuộc cạnh \(AB\). Gọi \(\left( \alpha \right)\) là mặt phẳng qua \(M\), song song với hai đường thẳng \(BC\) và \(AD\). Gọi \(N,P,Q\) lần lượt là giao điểm của mặt phẳng \(\left( \alpha \right)\) với các cạnh \(AC,CD\) và \(DB\).

a) Chứng minh \(MNPQ\) là hình bình hành.

b) Trong trường hợp nào thì \(MNPQ\) là hình thoi?

Phương pháp giải - Xem chi tiết Bài 4 trang 112 SGK Toán 11 tập 1 - Chân trời sáng tạo 1

Áp dụng định lí 2: Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song.

Lời giải chi tiết

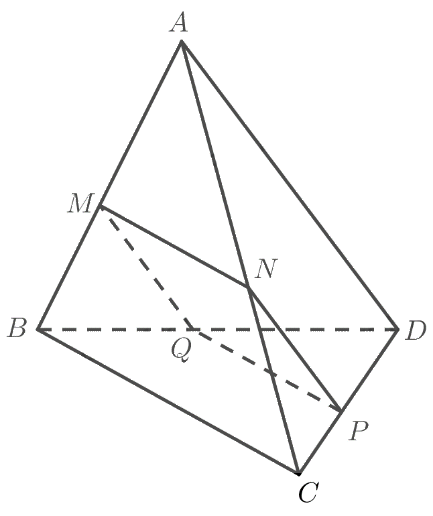
Bài 4 trang 112 SGK Toán 11 tập 1 - Chân trời sáng tạo 2

a) Ta có:

\(\begin{array}{l}MN = \left( \alpha \right) \cap \left( {ABC} \right)\\PQ = \left( \alpha \right) \cap \left( {BC{\rm{D}}} \right)\\BC = \left( {ABC} \right) \cap \left( {BC{\rm{D}}} \right)\\MN\parallel BC\end{array}\)

Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(MN\parallel PQ\parallel BC\) (1).

\(\begin{array}{l}MQ = \left( \alpha \right) \cap \left( {ABD} \right)\\NP = \left( \alpha \right) \cap \left( {AC{\rm{D}}} \right)\\A{\rm{D}} = \left( {ABD} \right) \cap \left( {AC{\rm{D}}} \right)\\MQ\parallel A{\rm{D}}\end{array}\)

Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(MQ\parallel NP\parallel A{\rm{D}}\) (2).

Từ (1) và (2) suy ra \(MNPQ\) là hình bình hành.

b) Để \(MNPQ\) là hình thoi thì \(MN = NP\).

Ta có:

\(\begin{array}{l}MN\parallel BC \Rightarrow \frac{{MN}}{{BC}} = \frac{{AN}}{{AC}}\\NP\parallel A{\rm{D}} \Rightarrow \frac{{NP}}{{A{\rm{D}}}} = \frac{{CN}}{{AC}} \Rightarrow \frac{{MN}}{{A{\rm{D}}}} = \frac{{CN}}{{AC}}\end{array}\)

Ta có:

\(\begin{array}{l}\frac{{AN}}{{AC}} + \frac{{CN}}{{AC}} = 1 \Leftrightarrow \frac{{MN}}{{BC}} + \frac{{MN}}{{A{\rm{D}}}} = 1 \Leftrightarrow MN.\left( {\frac{1}{{BC}} + \frac{1}{{A{\rm{D}}}}} \right) = 1\\ \Leftrightarrow MN.\frac{{BC + A{\rm{D}}}}{{BC.A{\rm{D}}}} = 1 \Leftrightarrow MN = \frac{{BC.A{\rm{D}}}}{{BC + A{\rm{D}}}}\end{array}\)

Vậy nếu \(MN = \frac{{BC.A{\rm{D}}}}{{BC + A{\rm{D}}}}\) thì \(MNPQ\) là hình thoi.

Bài 4 trang 112 SGK Toán 11 Tập 1 - Chân trời sáng tạo: Giải chi tiết và hướng dẫn

Bài 4 trang 112 SGK Toán 11 Tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học về phép biến hóa lượng giác. Bài tập này yêu cầu học sinh phải nắm vững các công thức lượng giác cơ bản, đặc biệt là các công thức biến đổi lượng giác để giải phương trình.

Nội dung bài tập

Bài tập yêu cầu giải các phương trình lượng giác sau:

a) sin(x + π/3) = sin(x - π/4)
b) cos(2x - π/6) = cos(x + π/3)
c) tan(x + π/4) = tan(2x)

Phương pháp giải

Để giải các phương trình lượng giác này, chúng ta sẽ sử dụng các công thức sau:

sin(a) = sin(b) ⇔ a = b + k2π hoặc a = π - b + k2π (k ∈ Z)
cos(a) = cos(b) ⇔ a = b + k2π hoặc a = -b + k2π (k ∈ Z)
tan(a) = tan(b) ⇔ a = b + kπ (k ∈ Z)

Giải chi tiết

a) sin(x + π/3) = sin(x - π/4)

Áp dụng công thức sin(a) = sin(b), ta có:

x + π/3 = x - π/4 + k2π ⇔ π/3 = -π/4 + k2π ⇔ 7π/12 = k2π ⇔ k = 7/24 (không phải số nguyên, loại)
x + π/3 = π - (x - π/4) + k2π ⇔ x + π/3 = π - x + π/4 + k2π ⇔ 2x = π - π/3 - π/4 + k2π ⇔ 2x = 5π/12 + k2π ⇔ x = 5π/24 + kπ (k ∈ Z)

Vậy nghiệm của phương trình là x = 5π/24 + kπ (k ∈ Z).

b) cos(2x - π/6) = cos(x + π/3)

Áp dụng công thức cos(a) = cos(b), ta có:

2x - π/6 = x + π/3 + k2π ⇔ x = π/2 + k2π (k ∈ Z)
2x - π/6 = -(x + π/3) + k2π ⇔ 2x - π/6 = -x - π/3 + k2π ⇔ 3x = -π/3 + π/6 + k2π ⇔ 3x = -π/6 + k2π ⇔ x = -π/18 + k2π/3 (k ∈ Z)

Vậy nghiệm của phương trình là x = π/2 + k2π và x = -π/18 + k2π/3 (k ∈ Z).

c) tan(x + π/4) = tan(2x)

Áp dụng công thức tan(a) = tan(b), ta có:

x + π/4 = 2x + kπ ⇔ x = π/4 - kπ (k ∈ Z)

Vậy nghiệm của phương trình là x = π/4 - kπ (k ∈ Z).

Lưu ý quan trọng

Khi giải phương trình lượng giác, cần chú ý kiểm tra điều kiện xác định của hàm lượng giác. Ví dụ, với hàm tan(x), x ≠ π/2 + kπ (k ∈ Z).

Bài tập tương tự

Để rèn luyện thêm kỹ năng giải phương trình lượng giác, bạn có thể tham khảo các bài tập tương tự trong SGK Toán 11 Tập 1 - Chân trời sáng tạo hoặc trên các trang web học toán trực tuyến.

tusach.vn hy vọng với lời giải chi tiết này, bạn sẽ hiểu rõ hơn về cách giải Bài 4 trang 112 SGK Toán 11 Tập 1 - Chân trời sáng tạo và tự tin hơn trong các kỳ thi sắp tới.