Bài 11 Trang 87 Toán 11 Tập 2 – Chân Trời Sáng Tạo

Bài 11 trang 87 SGK Toán 11 tập 2 – Chân trời sáng tạo

Bài 11 trang 87 SGK Toán 11 tập 2 thuộc chương trình Toán 11 Chân trời sáng tạo, tập trung vào việc ôn tập chương 3: Hàm số lượng giác. Bài tập này yêu cầu học sinh vận dụng kiến thức về các hàm số lượng giác cơ bản, tính chất của chúng và các phương pháp giải phương trình lượng giác.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\)

Đề bài

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\); \(AB = AD = 2a;CD = a\); số đo góc nhị diện \(\left[ {S,BC,A} \right]\) bằng \({60^ \circ }\). Gọi \(I\) là trung điểm của cạnh \(A{\rm{D}}\). Biết hai mặt phẳng \(\left( {SBI} \right)\) và \(\left( {SCD} \right)\) cùng vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Tính thể tích khối chóp \(S.ABCD\) theo \(a\).

Phương pháp giải - Xem chi tiết Bài 11 trang 87 SGK Toán 11 tập 2 – Chân trời sáng tạo 1

Sử dụng công thức tính thể tích khối chóp: \(V = \frac{1}{3}Sh\).

Lời giải chi tiết

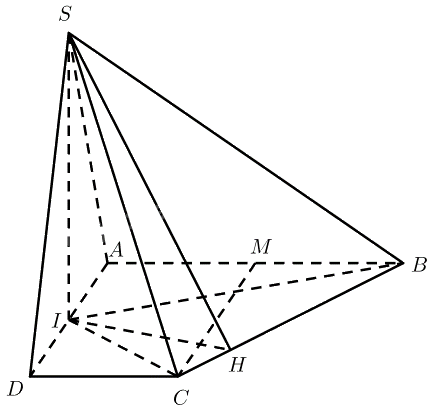
Bài 11 trang 87 SGK Toán 11 tập 2 – Chân trời sáng tạo 2

\(\left. \begin{array}{l}\left( {SBI} \right) \bot \left( {ABCD} \right)\\\left( {SCI} \right) \bot \left( {ABCD} \right)\\\left( {SBI} \right) \cap \left( {SCI} \right) = SI\end{array} \right\} \Rightarrow SI \bot \left( {ABCD} \right)\)

Kẻ \(IH \bot BC\left( {H \in BC} \right)\)

\(SI \bot \left( {ABCD} \right) \Rightarrow SI \bot BC\)

\( \Rightarrow BC \bot \left( {SIH} \right) \Rightarrow BC \bot SH\)

Vậy \(\widehat {AHI}\) là góc nhị diện \(\left[ {S,BC,A} \right]\)\( \Rightarrow \widehat {AHI} = {60^ \circ }\)

\(\begin{array}{l}{S_{ABC{\rm{D}}}} = \frac{1}{2}\left( {AB + C{\rm{D}}} \right).A{\rm{D}} = 3{a^2}\\AI = I{\rm{D}} = \frac{1}{2}A{\rm{D}} = a\\{S_{AIB}} = \frac{1}{2}AB.AI = {a^2},{S_{CI{\rm{D}}}} = \frac{1}{2}C{\rm{D}}.I{\rm{D}} = \frac{{{a^2}}}{2}\\ \Rightarrow {S_{BIC}} = {S_{ABC{\rm{D}}}} - {S_{AIB}} - {S_{CI{\rm{D}}}} = \frac{{3{a^2}}}{2}\end{array}\)

Gọi \(M\) là trung điểm của \(AB\)

\(\begin{array}{l} \Rightarrow BM = \frac{1}{2}AB = a,CM = AD = 2a \Rightarrow BC = \sqrt {B{M^2} + C{M^2}} = a\sqrt 5 \\ \Rightarrow IH = \frac{{2{{\rm{S}}_{BIC}}}}{{BC}} = \frac{{3a\sqrt 5 }}{5} \Rightarrow SI = IH.\tan \widehat {SHI} = \frac{{3a\sqrt {15} }}{5}\end{array}\)

\({V_{S.ABC{\rm{D}}}} = \frac{1}{3}{S_{ABC{\rm{D}}}}.SI = \frac{{3{a^3}\sqrt {15} }}{5}\)

Bài 11 Trang 87 SGK Toán 11 Tập 2 – Chân Trời Sáng Tạo: Giải Chi Tiết và Hướng Dẫn

Bài 11 trang 87 SGK Toán 11 tập 2 – Chân trời sáng tạo là một bài tập quan trọng trong chương trình ôn tập chương 3 về hàm số lượng giác. Bài tập này không chỉ giúp học sinh củng cố kiến thức đã học mà còn rèn luyện kỹ năng giải toán, đặc biệt là các bài toán liên quan đến phương trình lượng giác và ứng dụng của hàm số lượng giác.

Nội dung chính của Bài 11 trang 87

Bài 11 thường bao gồm các dạng bài tập sau:

Giải phương trình lượng giác: Yêu cầu học sinh giải các phương trình lượng giác cơ bản và nâng cao, sử dụng các công thức lượng giác và phương pháp biến đổi tương đương.
Tìm tập nghiệm của phương trình lượng giác: Xác định tập nghiệm của phương trình lượng giác trong một khoảng hoặc trên toàn bộ trục số.
Ứng dụng hàm số lượng giác vào thực tế: Giải các bài toán thực tế liên quan đến góc, độ cao, khoảng cách và các yếu tố khác, sử dụng kiến thức về hàm số lượng giác để mô tả và giải quyết vấn đề.

Hướng dẫn giải chi tiết

Để giải quyết bài 11 trang 87 một cách hiệu quả, học sinh cần:

Nắm vững kiến thức cơ bản: Hiểu rõ định nghĩa, tính chất và các công thức lượng giác cơ bản.
Luyện tập thường xuyên: Giải nhiều bài tập tương tự để làm quen với các dạng bài và phương pháp giải.
Sử dụng các công cụ hỗ trợ: Sử dụng máy tính bỏ túi hoặc các phần mềm toán học để kiểm tra kết quả và tìm kiếm các phương pháp giải khác.

Ví dụ minh họa (Giả định một phần của bài tập)

Ví dụ: Giải phương trình 2sin(x) - 1 = 0

Lời giải:

2sin(x) - 1 = 0

sin(x) = 1/2

x = π/6 + k2π hoặc x = 5π/6 + k2π (k ∈ Z)

Tầm quan trọng của việc giải bài tập

Việc giải bài tập, đặc biệt là các bài tập trong SGK Toán 11 tập 2 – Chân trời sáng tạo, có vai trò quan trọng trong việc:

Củng cố kiến thức: Giúp học sinh hiểu sâu hơn về các khái niệm và công thức lượng giác.
Rèn luyện kỹ năng: Phát triển kỹ năng giải toán, tư duy logic và khả năng áp dụng kiến thức vào thực tế.
Chuẩn bị cho kỳ thi: Giúp học sinh tự tin hơn khi làm bài thi Toán 11 và các kỳ thi quan trọng khác.

Tại sao nên chọn tusach.vn để học Toán 11?

tusach.vn là một website học tập trực tuyến uy tín, cung cấp:

Lời giải chi tiết và dễ hiểu: Được trình bày rõ ràng, logic, giúp học sinh dễ dàng nắm bắt kiến thức.
Đội ngũ giáo viên giàu kinh nghiệm: Đảm bảo chất lượng và độ chính xác của nội dung.
Giao diện thân thiện và dễ sử dụng: Tạo trải nghiệm học tập tốt nhất cho học sinh.
Cập nhật liên tục: Cung cấp lời giải mới nhất cho các bài tập trong SGK và các đề thi thử.

Hãy truy cập tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích và nâng cao kết quả học tập của bạn!

Hàm số	Tập xác định
sin(x)	R
cos(x)	R

Bài 11 trang 87 SGK Toán 11 tập 2 – Chân trời sáng tạo

Bài 11 trang 87 SGK Toán 11 tập 2 – Chân trời sáng tạo

Bài 11 Trang 87 SGK Toán 11 Tập 2 – Chân Trời Sáng Tạo: Giải Chi Tiết và Hướng Dẫn

Nội dung chính của Bài 11 trang 87

Hướng dẫn giải chi tiết

Ví dụ minh họa (Giả định một phần của bài tập)

Tầm quan trọng của việc giải bài tập

Tại sao nên chọn tusach.vn để học Toán 11?

CHỦ ĐỀ SÁCH XEM NHIỀU

VỀ TUSACH.VN