Giải mục 3 trang 94, 95 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 3 trang 94, 95 SGK Toán 11 tập 1 - Chân trời sáng tạo
Chào mừng bạn đến với lời giải chi tiết mục 3 trang 94, 95 sách giáo khoa Toán 11 tập 1 chương trình Chân trời sáng tạo. Tại tusach.vn, chúng tôi luôn cố gắng cung cấp những giải pháp học tập hiệu quả và dễ hiểu nhất cho các em học sinh.
Bài viết này sẽ giúp bạn hiểu rõ cách giải các bài tập trong mục 3, từ đó củng cố kiến thức và tự tin hơn trong quá trình học tập.
Cho đường thẳng \(a\) và điểm \(A\) không nằm trên \(a\). Trên \(a\) lấy hai điểm \(B,C\). Đường thẳng \(a\) có nằm trong mặt phẳng \(\left( {ABC} \right)\) không? Giải thích.
Hoạt động 8
Cho đường thẳng \(a\) và điểm \(A\) không nằm trên \(a\). Trên \(a\) lấy hai điểm \(B,C\). Đường thẳng \(a\) có nằm trong mặt phẳng \(\left( {ABC} \right)\) không? Giải thích.
Phương pháp giải:
Áp dụng các tính chất:
‒ Tính chất 2: Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.
‒ Tính chất 3: Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.
Lời giải chi tiết:
Áp dụng tính chất 2, ta có duy nhất một mặt phẳng đi qua ba điểm phân biệt \(A,B,C\) là mặt phẳng \(\left( {ABC} \right)\).
Áp dụng tính chất 3, ta có đường thẳng \(a\) có hai điểm phân biệt \(B,C\) nằm trong mặt phẳng \(\left( {ABC} \right)\) nên mọi điểm của đường thẳng \(a\) cũng nằm trong mặt phẳng \(\left( {ABC} \right)\). Vậy đường thẳng \(a\) nằm trong mặt phẳng \(\left( {ABC} \right)\).
Hoạt động 9
Hai đường thẳng phân biệt \(a\) và \(b\) cắt nhau tại điểm \(O\). Trên \(a,b\) lấy lần lượt hai điểm \(M,N\) khác \(O\). Gọi \(\left( P \right)\) là mặt phẳng đi qua ba điểm \(M,N,O\) (Hình 25). Mặt phẳng \(\left( P \right)\) có chứa cả hai đường thẳng \(a\) và \(b\) không? Giải thích.
Phương pháp giải:
Áp dụng các tính chất:
‒ Tính chất 2: Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.
‒ Tính chất 3: Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.
Lời giải chi tiết:
Áp dụng tính chất 2, ta có \(\left( P \right)\) là mặt phẳng duy nhất đi qua ba điểm phân biệt \(A,B,C\) là mặt phẳng \(M,N,O\).
Áp dụng tính chất 3, ta có
– Đường thẳng \(a\) có hai điểm phân biệt \(M,O\) nằm trong mặt phẳng \(\left( P \right)\) nên mọi điểm của đường thẳng \(a\) cũng nằm trong mặt phẳng \(\left( P \right)\). Vậy đường thẳng \(a\) nằm trong mặt phẳng \(\left( P \right)\).
– Đường thẳng \(b\) có hai điểm phân biệt \(N,O\) nằm trong mặt phẳng \(\left( P \right)\) nên mọi điểm của đường thẳng \(b\) cũng nằm trong mặt phẳng \(\left( P \right)\). Vậy đường thẳng \(b\) nằm trong mặt phẳng \(\left( P \right)\).
Thực hành 7
Cho hai đường thẳng \(a\) và \(b\) cắt nhau tại \(O\) và điểm \(M\) không thuộc \(mp\left( {a,b} \right)\).
a) Tìm giao tuyến của hai mặt phẳng \(\left( {M,a} \right)\) và \(\left( {M,b} \right)\).
b) Lấy \(A,B\) lần lượt là hai điểm trên \(a,b\) và khác với điểm \(O\). Tìm giao tuyến của \(\left( {MAB} \right)\) và \(mp\left( {a,b} \right)\).
c) Lấy điểm \(A'\) trên đoạn \(MA\) và điểm \(B'\) trên đoạn \(MB\) sao cho đường thẳng \(A'B'\) cắt \(mp\left( {a,b} \right)\) tại \(C\). Chứng minh ba điểm \(A,B,C\) thẳng hàng.
Phương pháp giải:
‒ Để tìm giao tuyến của hai mặt phẳng, ta tìm hai điểm chung phân biệt của hai mặt phẳng đó.
‒ Để chứng minh ba điểm thẳng hàng, ta chứng minh ba điểm đó cùng thuộc giao tuyến của hai mặt phẳng.
Lời giải chi tiết:
a) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}M \in \left( {M,a} \right)\\M \in \left( {M,b} \right)\end{array} \right\} \Rightarrow M \in \left( {M,a} \right) \cap \left( {M,b} \right)\\\left. \begin{array}{l}O \in a \subset \left( {M,a} \right)\\O \in b \subset \left( {M,b} \right)\end{array} \right\} \Rightarrow O \in \left( {M,a} \right) \cap \left( {M,b} \right)\end{array}\)
Vậy giao tuyến của hai mặt phẳng \(\left( {M,a} \right)\) và \(\left( {M,b} \right)\) là đường thẳng \(MO\).
b) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}A \in \left( {MAB} \right)\\A \in a \subset \left( {a,b} \right)\end{array} \right\} \Rightarrow A \in \left( {MAB} \right) \cap \left( {a,b} \right)\\\left. \begin{array}{l}B \in \left( {MAB} \right)\\B \in b \subset \left( {a,b} \right)\end{array} \right\} \Rightarrow B \in \left( {MAB} \right) \cap \left( {a,b} \right)\end{array}\)
Vậy giao tuyến của hai mặt phẳng \(\left( {MAB} \right)\) và \(\left( {a,b} \right)\) là đường thẳng \(AB\) (1).
c) Ta có:
\(\left. \begin{array}{l}A' \in MA \subset \left( {MAB} \right)\\B' \in MB \subset \left( {MAB} \right)\end{array} \right\} \Rightarrow A'B' \subset \left( {MAB} \right)\)
Vì \(C \in A'B' \subset \left( {MAB} \right)\) và \(C \in mp\left( {a,b} \right)\) nên điểm \(C\) nằm trên giao tuyến của hai mặt phẳng \(\left( {MAB} \right)\) và \(\left( {a,b} \right)\) (2).
Từ (1) và (2) suy ra ba điểm \(A,B,C\) thẳng hàng.
Vận dụng 2
Giải thích tại sao ghế bốn chân có thể bị khập khiễng còn ghế ba chân thì không.
Phương pháp giải:
Áp dụng các tính chất:
‒ Tính chất 2: Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.
‒ Tính chất 4: Tồn tại bốn điểm không cùng nằm trên một mặt phẳng.
Lời giải chi tiết:
‒ Với ghế 4 chân, nếu 4 điểm tại chân ghế không thuộc một mặt phẳng thì ghế có thể bị khập khiễng.
‒ Với ghế 3 chân, ta chỉ xác định được duy nhất một mặt phẳng đi qua 3 điểm thuộc chân ghế nên ghế ba chân không thể khập khiễng.
Vận dụng 4
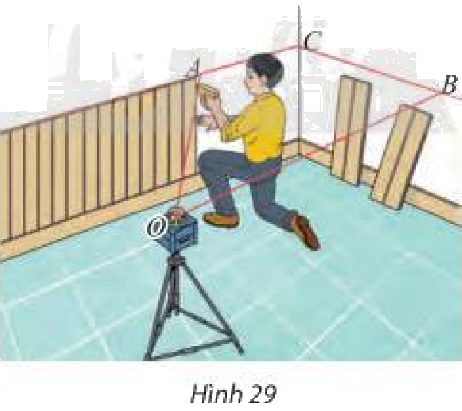
Trong xây dựng, người ta thường dùng máy quét tia laser để kẻ các đường thẳng trên tường hoặc sàn nhà. Tìm giao tuyến của mặt phẳng tạo bởi các tia laser \(OA\) và \(OB\) với các mặt tường trong Hình 29.

Phương pháp giải:
Quan sát hình ảnh và trả lời câu hỏi.
Lời giải chi tiết:
Từ Hình 29 ta thấy: Giao tuyến của mặt phẳng tạo bởi các tia laser \(OA\) và \(OB\) với các mặt tường là \(AC\) và \(BC\).
Giải mục 3 trang 94, 95 SGK Toán 11 tập 1 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 3 trang 94, 95 SGK Toán 11 tập 1 chương trình Chân trời sáng tạo tập trung vào việc ứng dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Đây là một phần quan trọng trong chương trình học, giúp học sinh rèn luyện kỹ năng phân tích, suy luận và giải quyết vấn đề.
Nội dung chính của Mục 3
Mục 3 bao gồm các bài tập liên quan đến:
- Xác định các hệ số a, b, c của hàm số bậc hai.
- Tìm tập xác định của hàm số.
- Xác định đỉnh, trục đối xứng và các điểm đặc biệt của parabol.
- Vẽ đồ thị hàm số bậc hai.
- Giải các bài toán liên quan đến ứng dụng của hàm số bậc hai trong thực tế.
Hướng dẫn giải chi tiết các bài tập
Dưới đây là hướng dẫn giải chi tiết từng bài tập trong mục 3 trang 94, 95 SGK Toán 11 tập 1:
Bài 1: Xác định hệ số a, b, c
Để xác định hệ số a, b, c của hàm số bậc hai, bạn cần đưa hàm số về dạng tổng quát: y = ax2 + bx + c. Sau đó, so sánh với dạng tổng quát để xác định giá trị của a, b, c.
Bài 2: Tìm tập xác định
Tập xác định của hàm số bậc hai là tập hợp tất cả các giá trị của x mà tại đó hàm số có nghĩa. Trong hầu hết các trường hợp, tập xác định của hàm số bậc hai là tập R (tập hợp tất cả các số thực).
Bài 3: Xác định đỉnh, trục đối xứng
Đỉnh của parabol là điểm có tọa độ (x0, y0), trong đó x0 = -b/2a và y0 = f(x0). Trục đối xứng của parabol là đường thẳng x = x0.
Bài 4: Vẽ đồ thị hàm số
Để vẽ đồ thị hàm số bậc hai, bạn cần xác định đỉnh, trục đối xứng, các điểm đặc biệt (giao điểm với trục Ox, trục Oy) và một vài điểm khác trên đồ thị. Sau đó, nối các điểm này lại với nhau để tạo thành parabol.
Mẹo giải nhanh và hiệu quả
Để giải các bài tập trong mục 3 một cách nhanh chóng và hiệu quả, bạn có thể áp dụng một số mẹo sau:
- Nắm vững các công thức và định lý liên quan đến hàm số bậc hai.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng máy tính bỏ túi để tính toán nhanh chóng và chính xác.
- Kiểm tra lại kết quả sau khi giải xong bài tập.
Ứng dụng của hàm số bậc hai trong thực tế
Hàm số bậc hai có rất nhiều ứng dụng trong thực tế, ví dụ như:
- Tính quỹ đạo của vật ném.
- Tính diện tích của các hình học.
- Mô tả sự thay đổi của các đại lượng vật lý.
Bài tập vận dụng nâng cao
Để củng cố kiến thức và rèn luyện kỹ năng, bạn có thể thử giải các bài tập vận dụng nâng cao sau:
- Tìm giá trị của m để hàm số y = (m-1)x2 + 2mx + 3 có đỉnh nằm trên trục Ox.
- Tìm giá trị của m để hàm số y = x2 - 2(m+1)x + m2 + 2m luôn dương.
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức hữu ích và giúp bạn giải quyết các bài tập trong mục 3 trang 94, 95 SGK Toán 11 tập 1 chương trình Chân trời sáng tạo một cách dễ dàng và hiệu quả. Chúc bạn học tập tốt!