Giải mục 1 trang 71, 72 SGK Toán 11 tập 1 - Chân trời sáng tạo

Chào mừng bạn đến với lời giải chi tiết mục 1 trang 71, 72 sách giáo khoa Toán 11 tập 1 chương trình Chân trời sáng tạo. Tại tusach.vn, chúng tôi luôn cố gắng cung cấp những lời giải chính xác, dễ hiểu nhất để hỗ trợ quá trình học tập của bạn.

Bài tập trong mục này tập trung vào việc... (nêu ngắn gọn nội dung chính của mục 1)

Xét hàm số \(y = f\left( x \right) = \frac{{2{x^2} - 2}}{{x - 1}}\).

Hoạt động 1

Xét hàm số \(y = f\left( x \right) = \frac{{2{x^2} - 2}}{{x - 1}}\).

a) Bảng sau đây cho biết giá trị của hàm số tại một số điểm gần điểm 1.

Giải mục 1 trang 71, 72 SGK Toán 11 tập 1 - Chân trời sáng tạo 1

Có nhận xét gì về giá trị của hàm số khi \(x\) càng gần đến 1?

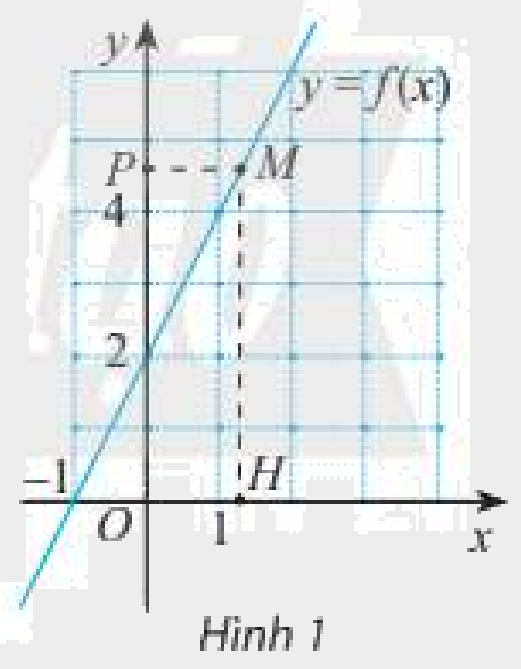
b) Ở Hình 1, \(M\) là điểm trên đồ thị hàm số \(y = f\left( x \right)\); \(H\) và \(P\) lần lượt là hình chiếu của điểm \(M\) trên trục hoành và trục tung. Khi điểm \(H\) thay đổi gần về điểm \(\left( {1;0} \right)\) trên trục hoành thì điểm \(P\) thay đổi như thế nào?

Giải mục 1 trang 71, 72 SGK Toán 11 tập 1 - Chân trời sáng tạo 2

Phương pháp giải:

Quan sát đồ thị và nhận xét.

Lời giải chi tiết:

a) Khi \(x\) càng gần đến 1 thì giá trị của hàm số càng gần đến 4.

b) Khi điểm \(H\) thay đổi gần về điểm \(\left( {1;0} \right)\) trên trục hoành thì điểm \(P\) càng gần đến điểm \(\left( {0;4} \right)\).

Thực hành 1

Tính các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to 3} \left( {2{x^2} - x} \right)\);

b) \(\mathop {\lim }\limits_{x \to - 1} \frac{{{x^2} + 2x + 1}}{{x + 1}}\).

Phương pháp giải:

Đưa về tính giới hạn của dãy số \(\left( {{x_n}} \right)\) thỏa mãn \({x_n} \to {x_0}\) khi \(n \to + \infty \).

Lời giải chi tiết:

a) Đặt \(f\left( x \right) = 2{x^2} - x\).

Hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\).

Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì thỏa mãn \({x_n} \to 3\) khi \(n \to + \infty \). Ta có:

\(\lim f\left( {{x_n}} \right) = \lim \left( {2x_n^2 - {x_n}} \right) = 2.\lim x_n^2 - \lim {x_n} = {2.3^2} - 3 = 15\).

Vậy \(\mathop {\lim }\limits_{x \to 3} \left( {2{x^2} - x} \right) = 15\).

b) Đặt \(f\left( x \right) = \frac{{{x^2} + 2x + 1}}{{x + 1}}\).

Hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\).

Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì thỏa mãn \({x_n} \to - 1\) khi \(n \to + \infty \). Ta có:

\(\lim f\left( {{x_n}} \right) = \lim \frac{{x_n^2 + 2{x_n} + 1}}{{{x_n} + 1}} = \lim \frac{{{{\left( {{x_n} + 1} \right)}^2}}}{{{x_n} + 1}} = \lim \left( {{x_n} + 1} \right) = \lim {x_n} + 1 = - 1 + 1 = 0\).

Vậy \(\mathop {\lim }\limits_{x \to - 1} \frac{{{x^2} + 2x + 1}}{{x + 1}} = 0\).

Giải mục 1 trang 71, 72 SGK Toán 11 tập 1 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết

Mục 1 trang 71, 72 SGK Toán 11 tập 1 chương trình Chân trời sáng tạo là một phần quan trọng trong chương học về hàm số lượng giác. Nội dung chính của mục này xoay quanh việc ôn tập lại các kiến thức cơ bản về hàm số lượng giác, đặc biệt là các hàm sin, cosin, tang và cotang, cùng với các tính chất và ứng dụng của chúng. Việc nắm vững kiến thức này là nền tảng để giải quyết các bài tập phức tạp hơn trong chương trình học.

Nội dung chính của Mục 1

Ôn tập về hàm số lượng giác: Nhắc lại định nghĩa, tập xác định, tập giá trị, tính tuần hoàn và tính chẵn lẻ của các hàm sin, cosin, tang và cotang.
Đồ thị hàm số lượng giác: Phân tích hình dạng, các điểm đặc biệt và các tính chất quan trọng của đồ thị hàm số lượng giác.
Ứng dụng của hàm số lượng giác: Giải các bài toán thực tế liên quan đến hàm số lượng giác, ví dụ như tính chiều cao của một tòa nhà, đo khoảng cách giữa hai điểm, hoặc mô tả các hiện tượng tuần hoàn trong tự nhiên.

Hướng dẫn giải chi tiết các bài tập trong Mục 1

Dưới đây là hướng dẫn giải chi tiết từng bài tập trong mục 1 trang 71, 72 SGK Toán 11 tập 1 Chân trời sáng tạo:

Bài 1: (Ví dụ minh họa)

Đề bài: Giải phương trình sin(x) = 1/2.

Lời giải:

Tìm các giá trị x sao cho sin(x) = 1/2.
Sử dụng đường tròn lượng giác hoặc kiến thức về các góc đặc biệt để tìm ra các nghiệm của phương trình.
Viết tập nghiệm của phương trình.

Bài 2: (Ví dụ minh họa)

Đề bài: Vẽ đồ thị hàm số y = cos(x) trên khoảng [-π, π].

Lời giải:

Lập bảng giá trị của hàm số y = cos(x) với các giá trị x thuộc khoảng [-π, π].
Vẽ hệ trục tọa độ và đánh dấu các điểm tương ứng với bảng giá trị.
Nối các điểm lại với nhau để tạo thành đồ thị hàm số.

Mẹo giải bài tập hiệu quả

Để giải các bài tập về hàm số lượng giác một cách hiệu quả, bạn nên:

Nắm vững các định nghĩa, tính chất và công thức liên quan đến hàm số lượng giác.
Sử dụng đường tròn lượng giác để hình dung và giải quyết các bài toán.
Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Sử dụng máy tính bỏ túi để kiểm tra lại kết quả.

Tài liệu tham khảo hữu ích

Ngoài SGK Toán 11 tập 1 Chân trời sáng tạo, bạn có thể tham khảo thêm các tài liệu sau:

Sách bài tập Toán 11
Các trang web học toán trực tuyến
Các video hướng dẫn giải bài tập trên YouTube

Hy vọng rằng với hướng dẫn chi tiết này, bạn sẽ tự tin hơn trong việc giải các bài tập mục 1 trang 71, 72 SGK Toán 11 tập 1 Chân trời sáng tạo. Chúc bạn học tập tốt!

Giải mục 1 trang 71, 72 SGK Toán 11 tập 1 - Chân trời sáng tạo

Giải mục 1 trang 71, 72 SGK Toán 11 tập 1 - Chân trời sáng tạo

Hoạt động 1

Thực hành 1

Giải mục 1 trang 71, 72 SGK Toán 11 tập 1 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết

Nội dung chính của Mục 1

Hướng dẫn giải chi tiết các bài tập trong Mục 1

Bài 1: (Ví dụ minh họa)

Bài 2: (Ví dụ minh họa)

Mẹo giải bài tập hiệu quả

Tài liệu tham khảo hữu ích

CHỦ ĐỀ SÁCH XEM NHIỀU

VỀ TUSACH.VN