Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải mục 1 trang 54, 55 SGK Toán 11 tập 2 - Chân trời sáng tạo
SGK Toán 11 - Chân trời sáng tạo
Giải Toán 11 tập 2 - Chân trời sáng tạo
Chương VIII. Quan hệ vuông góc trong không gian. Phép chiếu song song
Bài 1. Hai đường thẳng vuông góc

Giải mục 1 trang 54, 55 SGK Toán 11 tập 2 - Chân trời sáng tạo

Giải mục 1 trang 54, 55 SGK Toán 11 tập 2 - Chân trời sáng tạo

Chào mừng bạn đến với lời giải chi tiết mục 1 trang 54, 55 SGK Toán 11 tập 2, chương trình Chân trời sáng tạo. Bài viết này sẽ cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập hiệu quả.

Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn. Vì vậy, tusach.vn luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ bạn học tốt môn Toán 11.

Cho hai đường thẳng chéo nhau (a) và (b) trong không gian. Qua một điểm (M)

Hoạt động 1Thực hành 1Vận dụng 1

Hoạt động 1

    Cho hai đường thẳng chéo nhau \(a\) và \(b\) trong không gian. Qua một điểm \(M\) tuỳ ý vẽ \(a'\parallel a\) và vẽ \(b'\parallel b\). Khi thay đổi vị trí của điểm \(M\), có nhận xét gì về góc giữa \(a'\) và \(b'\)?

    Phương pháp giải:

    Quan sát hình ảnh và nhận xét.

    Lời giải chi tiết:

    Khi thay đổi vị trí của điểm \(M\), góc giữa \(a'\) và \(b'\) không đổi.

    Thực hành 1

      Cho hình hộp \(ABCD.A'B'C'D'\) có 6 mặt đều là hình vuông \(M,N,E,F\) lần lượt là trung điểm các cạnh \(BC,BA,AA',A'D'\). Tính góc giữa các cặp đường thẳng:

      a) \(MN\) và \(DD'\);

      b) \(MN\) và \(CD'\);

      c) \(EF\) và \(CC'\).

      Phương pháp giải:

      Cách xác định góc giữa hai đường thẳng \(a\) và \(b\):

      Bước 1: Lấy một điểm \(O\) bất kì.

      Bước 2: Qua điểm \(O\) dựng đường thẳng \(a'\parallel a\) và đường thẳng \(b'\parallel b\).

      Bước 3: Tính \(\left( {a,b} \right) = \left( {a',b'} \right)\).

      Lời giải chi tiết:

      Giải mục 1 trang 54, 55 SGK Toán 11 tập 2 - Chân trời sáng tạo 1

      a) Ta có: \(M\) là trung điểm của \(BC\)

      \(N\) là trung điểm của \(AB\)

      \( \Rightarrow MN\) là đường trung bình của tam giác \(ABC\)

      \( \Rightarrow MN\parallel AC\)

      Mà \(DD'\parallel AA'\)

      \( \Rightarrow \left( {MN,DD'} \right) = \left( {AC,AA'} \right) = \widehat {A'AC} = {90^ \circ }\).

      b) Ta có: \(MN\parallel AC\)

      \( \Rightarrow \left( {MN,CD'} \right) = \left( {AC,C{\rm{D}}'} \right) = \widehat {AC{\rm{D}}'}\)

      Vì \(ABC{\rm{D}},ADD'A',C{\rm{DD}}'{\rm{C}}'\) là các hình vuông bằng nhau nên các đường chéo của chúng bằng nhau. Vậy \(AC = A{\rm{D}}' = C{\rm{D}}'\)

      \( \Rightarrow \Delta AC{\rm{D}}'\) là tam giác đều \( \Rightarrow \widehat {AC{\rm{D}}'} = {60^ \circ }\).

      Vậy \(\left( {MN,CD'} \right) = {60^ \circ }\).

      Vận dụng 1

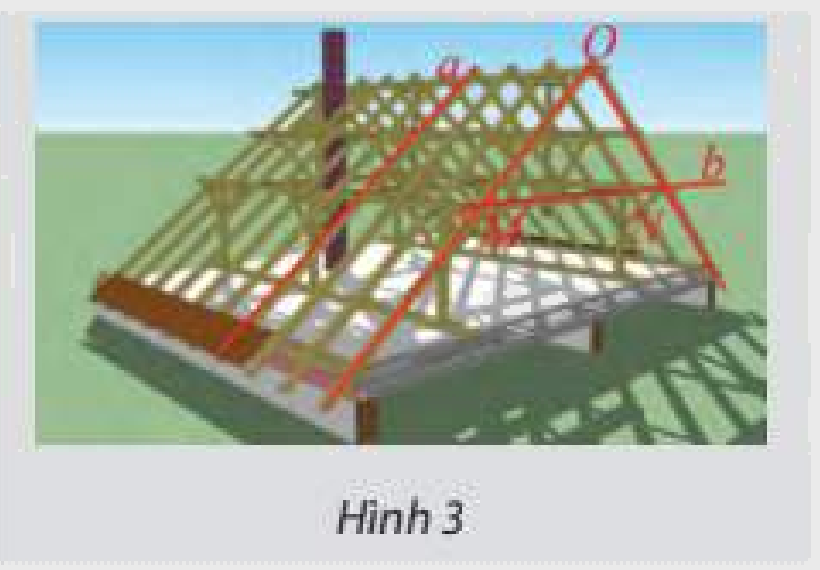
        Khung của một mái nhà được ghép bởi các thanh gỗ như Hình 3. Cho biết tam giác \(OMN\) vuông cân tại \(O\). Tính góc giữa hai thanh gỗ \(a\) và \(b\).

        Giải mục 1 trang 54, 55 SGK Toán 11 tập 2 - Chân trời sáng tạo 1

        Phương pháp giải:

        Cách xác định góc giữa hai đường thẳng \(a\) và \(b\):

        Bước 1: Lấy một điểm \(O\) bất kì.

        Bước 2: Qua điểm \(O\) dựng đường thẳng \(a'\parallel a\) và đường thẳng \(b'\parallel b\).

        Bước 3: Tính \(\left( {a,b} \right) = \left( {a',b'} \right)\).

        Lời giải chi tiết:

        Ta có: \(a\parallel OM \Rightarrow \left( {a,b} \right) = \left( {OM,b} \right) = \widehat {MON} = {90^ \circ }\).

        Giải mục 1 trang 54, 55 SGK Toán 11 tập 2 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết

        Mục 1 trang 54, 55 SGK Toán 11 tập 2 chương trình Chân trời sáng tạo thường tập trung vào các kiến thức về đạo hàm của hàm số. Đây là một phần quan trọng trong chương trình Toán 11, nền tảng cho các kiến thức nâng cao hơn ở các lớp trên. Việc nắm vững kiến thức và kỹ năng giải bài tập trong mục này là vô cùng cần thiết.

        Nội dung chính của Mục 1 trang 54, 55

        • Khái niệm đạo hàm: Định nghĩa đạo hàm của hàm số tại một điểm, ý nghĩa hình học và vật lý của đạo hàm.
        • Quy tắc tính đạo hàm: Các quy tắc tính đạo hàm của tổng, hiệu, tích, thương của các hàm số.
        • Đạo hàm của một số hàm số cơ bản: Đạo hàm của hàm số lũy thừa, hàm số lượng giác, hàm số mũ, hàm số logarit.
        • Ứng dụng của đạo hàm: Tìm cực trị của hàm số, khảo sát hàm số.

        Hướng dẫn giải chi tiết các bài tập trong Mục 1

        Dưới đây là hướng dẫn giải chi tiết các bài tập trong Mục 1 trang 54, 55 SGK Toán 11 tập 2 Chân trời sáng tạo:

        Bài 1: Tính đạo hàm của các hàm số sau:
        1. f(x) = x3 + 2x2 - 5x + 1
        2. g(x) = sin(x) + cos(x)
        3. h(x) = ex + ln(x)

        Giải:

        • f'(x) = 3x2 + 4x - 5
        • g'(x) = cos(x) - sin(x)
        • h'(x) = ex + 1/x
        Bài 2: Tìm đạo hàm của hàm số y = (x2 + 1)/(x - 1)

        Giải:

        Sử dụng quy tắc đạo hàm của thương:

        y' = [(x2 + 1)'(x - 1) - (x2 + 1)(x - 1)'] / (x - 1)2

        y' = [2x(x - 1) - (x2 + 1)] / (x - 1)2

        y' = (2x2 - 2x - x2 - 1) / (x - 1)2

        y' = (x2 - 2x - 1) / (x - 1)2

        Bài 3: Cho hàm số f(x) = x4 - 4x2 + 1. Tìm các điểm cực trị của hàm số.

        Giải:

        f'(x) = 4x3 - 8x

        Giải phương trình f'(x) = 0:

        4x3 - 8x = 0

        4x(x2 - 2) = 0

        x = 0 hoặc x = ±√2

        Khảo sát dấu của f'(x) để xác định các điểm cực trị.

        Kết luận: Hàm số có các điểm cực trị tại x = 0, x = √2, x = -√2.

        Mẹo học tốt Toán 11 chương trình Chân trời sáng tạo

        • Nắm vững định nghĩa và các quy tắc đạo hàm: Đây là nền tảng để giải các bài tập về đạo hàm.
        • Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài.
        • Sử dụng các tài liệu tham khảo: Sách giáo khoa, sách bài tập, các trang web học tập trực tuyến.
        • Hỏi thầy cô hoặc bạn bè khi gặp khó khăn: Đừng ngần ngại hỏi khi bạn không hiểu bài.

        Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về Mục 1 trang 54, 55 SGK Toán 11 tập 2 chương trình Chân trời sáng tạo. Chúc bạn học tốt!

        Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

        CHỦ ĐỀ SÁCH XEM NHIỀU

        Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

        VỀ TUSACH.VN