Bài 4 trang 74 Toán 11 Tập 2 - Chân trời sáng tạo

Bài 4 trang 74 SGK Toán 11 tập 2 – Chân trời sáng tạo

Bài 4 trang 74 SGK Toán 11 Tập 2 – Chân trời sáng tạo

Bài 4 trang 74 SGK Toán 11 Tập 2 thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để tìm đạo hàm của hàm số và giải các bài toán thực tế.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

Cho hình hộp đứng (ABCD.A'B'C'D') có đáy là hình thoi. Cho biết (AB = BD = a,A'C = 2a).

Đề bài

Cho hình hộp đứng \(ABCD.A'B'C'D'\) có đáy là hình thoi. Cho biết \(AB = BD = a,A'C = 2a\).

a) Tính độ dài đoạn thẳng \(AA'\).

b) Tính tổng diện tích các mặt của hình hộp.

Phương pháp giải - Xem chi tiết Bài 4 trang 74 SGK Toán 11 tập 2 – Chân trời sáng tạo 1

Sử dụng định lí Pitago.

Lời giải chi tiết

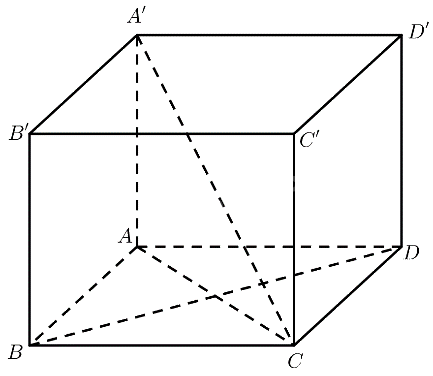
Bài 4 trang 74 SGK Toán 11 tập 2 – Chân trời sáng tạo 2

a) Xét tam giác \(AB{\rm{D}}\) có: \(AB = A{\rm{D}} = B{\rm{D}} = a\)

\( \Rightarrow \Delta AB{\rm{D}}\) đều \( \Rightarrow \widehat {BA{\rm{D}}} = {60^ \circ } \Rightarrow \widehat {ABC} = {180^ \circ } - \widehat {BA{\rm{D}}} = {120^ \circ }\)

Xét tam giác \(AB{\rm{C}}\) có:

\(AC = \sqrt {A{B^2} + B{C^2} - 2.AB.BC} = a\sqrt 3 \)

\(AA' \bot \left( {ABCD} \right) \Rightarrow AA' \bot AC \Rightarrow \Delta AA'C\) vuông tại \(A\)

\( \Rightarrow AA' = \sqrt {A'{C^2} - A{C^2}} = a\)

b) Ta có:

\(\begin{array}{l}{S_{ABC{\rm{D}}}} = {S_{A'B'C'D'}} = AB.AC.\sin \widehat {BAC} = \frac{{{a^2}\sqrt 3 }}{2}\\{S_{ABB'A'}} = {S_{C{\rm{DD}}'{\rm{C}}'}} = AB.AA' = {a^2}\\{S_{A{\rm{DD}}'A'}} = {S_{BCC'B'}} = A{\rm{D}}.AA' = {a^2}\end{array}\)

Tổng diện tích các mặt của hình hộp là:

\(S = {S_{ABC{\rm{D}}}} + {S_{A'B'C'D'}} + {S_{ABB'A'}} + {S_{C{\rm{DD}}'{\rm{C}}'}} + {S_{A{\rm{DD}}'A'}} + {S_{BCC'B'}} = 2.\frac{{{a^2}\sqrt 3 }}{2} + 4.{a^2} = \left( {4 + \sqrt 3 } \right){a^2}\)

Bài 4 trang 74 SGK Toán 11 Tập 2 – Chân trời sáng tạo: Giải chi tiết và hướng dẫn

Bài 4 trang 74 SGK Toán 11 Tập 2 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm của hàm số. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:

Nội dung bài tập

Bài 4 yêu cầu tính đạo hàm của các hàm số sau:

a) y = x³ - 3x² + 2x - 5
b) y = (x² + 1)(x - 2)
c) y = (x² + 3x)(x - 1)
d) y = x² + 1/x

Lời giải chi tiết

a) y = x³ - 3x² + 2x - 5

Áp dụng công thức đạo hàm của tổng và hiệu, ta có:

y' = 3x² - 6x + 2

b) y = (x² + 1)(x - 2)

Áp dụng công thức đạo hàm của tích, ta có:

y' = (2x)(x - 2) + (x² + 1)(1) = 2x² - 4x + x² + 1 = 3x² - 4x + 1

c) y = (x² + 3x)(x - 1)

Áp dụng công thức đạo hàm của tích, ta có:

y' = (2x + 3)(x - 1) + (x² + 3x)(1) = 2x² - 2x + 3x - 3 + x² + 3x = 3x² + 4x - 3

d) y = x² + 1/x

Áp dụng công thức đạo hàm của tổng và đạo hàm của 1/x, ta có:

y' = 2x - 1/x²

Lưu ý quan trọng

Nắm vững các công thức đạo hàm cơ bản: đạo hàm của tổng, hiệu, tích, thương, hàm hợp.
Chú ý áp dụng đúng công thức đạo hàm cho từng loại hàm số.
Kiểm tra lại kết quả sau khi tính đạo hàm.

Bài tập tương tự

Để rèn luyện thêm kỹ năng giải bài tập về đạo hàm, bạn có thể tham khảo các bài tập sau:

Tính đạo hàm của hàm số y = 2x⁴ - 5x³ + x - 7
Tính đạo hàm của hàm số y = (x + 2)(x² - 1)
Tính đạo hàm của hàm số y = x³ - 3x + 5/x²

Kết luận

Bài 4 trang 74 SGK Toán 11 Tập 2 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh hiểu rõ hơn về đạo hàm của hàm số. Việc nắm vững kiến thức và kỹ năng giải bài tập này sẽ giúp học sinh tự tin hơn trong quá trình học tập môn Toán.

tusach.vn hy vọng với lời giải chi tiết và hướng dẫn trên, các bạn học sinh sẽ giải bài tập này một cách dễ dàng và hiệu quả. Chúc các bạn học tốt!