Giải mục 4 trang 96, 97, 98 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 4 trang 96, 97, 98 SGK Toán 11 tập 1 - Chân trời sáng tạo
Chào mừng các em học sinh đến với lời giải chi tiết mục 4 trang 96, 97, 98 SGK Toán 11 tập 1, chương trình Chân trời sáng tạo. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Mục 4 này tập trung vào các bài tập về... (điền nội dung chính của mục 4 vào đây). Chúng tôi sẽ giải thích từng bước để các em hiểu rõ bản chất của bài toán.
a) Các công trình kiến trúc, đồ vật trong Hình 30 có mặt bên là hình gì?
Hoạt động 10
a) Các công trình kiến trúc, đồ vật trong Hình 30 có mặt bên là hình gì?
b) Tìm điểm giống nhau của các hình trong Hình 31.
Phương pháp giải:
Quan sát hình ảnh và trả lời câu hỏi.
Lời giải chi tiết:
a) Các công trình kiến trúc, đồ vật trong Hình 30 có mặt bên là hình tam giác.
b) Điểm giống nhau của các hình trong Hình 31 là: có các mặt bên là hình tam giác.
Hoạt động 11
Trong Hình 34, hình chóp nào có số mặt ít nhất?

Phương pháp giải:
Quan sát hình ảnh và đếm số mặt của hình.
Lời giải chi tiết:
Hình chóp a) có 4 mặt.
Hình chóp b) có 5 mặt.
Hình chóp c) có 6 mặt.
Hình chóp d) có 7 mặt.
Vậy hình a) có số mặt ít nhất.
Thực hành 8
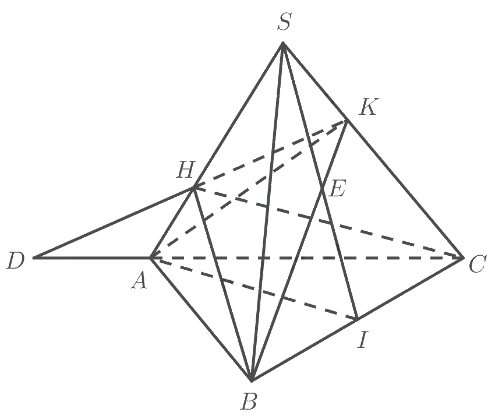
Cho tứ diện \(SABC\). Gọi \(H,K\) lần lượt là hai điểm trên hai cạnh \(SA\) và \(SC\left( {H \ne S,A;K \ne S,C} \right)\) sao cho \(HK\) không song song với \(AC\). Gọi \(I\) là trung điểm của \(BC\) (Hình 38).
a) Tìm giao điểm của đường thẳng \(HK\) và mặt phẳng \(\left( {ABC} \right)\).
b) Tìm giao tuyến của các mặt phẳng \(\left( {SAI} \right)\) và \(\left( {ABK} \right)\); \(\left( {SAI} \right)\) và \(\left( {BCH} \right)\).

Phương pháp giải:
‒ Để tìm giao điểm của đường thẳng và mặt phẳng, ta tìm giao điểm của đường thẳng đó với một đường thẳng trong mặt phẳng.
‒ Để tìm giao tuyến của hai mặt phẳng, ta tìm hai điểm chung phân biệt của hai mặt phẳng đó.
Lời giải chi tiết:

a) Gọi \(D = HK \cap AC\). Ta có:
\(\left. \begin{array}{l}D \in AC \subset \left( {ABC} \right)\\D \in HK\end{array} \right\} \Rightarrow M = HK \cap \left( {ABC} \right)\)
b) Gọi \(E = SI \cap BK\). Ta có:
\(\left. \begin{array}{l}E \in SI \subset \left( {SAI} \right)\\E \in BK \subset \left( {ABK} \right)\end{array} \right\} \Rightarrow E \in \left( {SAI} \right) \cap \left( {ABK} \right)\)
Mà \(A \in \left( {SAI} \right) \cap \left( {ABK} \right)\).
Vậy giao tuyến của hai mặt phẳng \(\left( {SAI} \right)\) và \(\left( {ABK} \right)\) là đường thẳng \(AE\).
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}I \in \left( {SAI} \right)\\I \in BC \subset \left( {BCH} \right)\end{array} \right\} \Rightarrow I \in \left( {SAI} \right) \cap \left( {BCH} \right)\\\left. \begin{array}{l}H \in SA \subset \left( {SAI} \right)\\H \in \left( {BCH} \right)\end{array} \right\} \Rightarrow H \in \left( {SAI} \right) \cap \left( {BCH} \right)\end{array}\)
Vậy giao tuyến của hai mặt phẳng \(\left( {SAI} \right)\) và \(\left( {BCH} \right)\) là đường thẳng \(HI\).
Vận dụng 4
Cho hình chóp \(S.ABCD\). Trên các cạnh bên của hình chóp lấy lần lượt các điểm \(A',B',C',D'\). Cho biết \(AC\) cắt \(B{\rm{D}}\) tại \(O\), \(A'C'\) cắt \(B'{\rm{D'}}\) tại \(O'\), \(AB\) cắt \(DC\) tại \(E\) và \(A'B'\) cắt \(D'C'\) tại \(E'\) (Hình 39). Chứng minh rằng:
a) \(S,O',O\) thẳng hàng;
b) \(S,E',E\) thẳng hàng.

Phương pháp giải:
Để chứng minh ba điểm thẳng hàng, ta chứng minh ba điểm đó cùng thuộc giao tuyến của hai mặt phẳng.
Lời giải chi tiết:
a) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}O \in AC \subset \left( {SAC} \right)\\O \in BD \subset \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow O \in \left( {SAC} \right) \cap \left( {SB{\rm{D}}} \right)\\\left. \begin{array}{l}O' \in A'C' \subset \left( {SAC} \right)\\O' \in B'D' \subset \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow O' \in \left( {SAC} \right) \cap \left( {SB{\rm{D}}} \right)\end{array}\)
Mà \(S \in \left( {SAC} \right) \cap \left( {SB{\rm{D}}} \right)\)
Do đó, \(S,O,O'\) cùng nằm trên giao tuyến của hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SB{\rm{D}}} \right)\).
Vậy \(S,O',O\) thẳng hàng.
b) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}E \in AB \subset \left( {SAB} \right)\\E \in CD \subset \left( {SC{\rm{D}}} \right)\end{array} \right\} \Rightarrow E \in \left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right)\\\left. \begin{array}{l}E' \in A'B' \subset \left( {SAB} \right)\\E' \in C'D' \subset \left( {SC{\rm{D}}} \right)\end{array} \right\} \Rightarrow E' \in \left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right)\end{array}\)
Mà \(S \in \left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right)\)
Do đó, \(S,E,E'\) cùng nằm trên giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SC{\rm{D}}} \right)\).
Vậy \(S,E,E'\) thẳng hàng.
Vận dụng 5
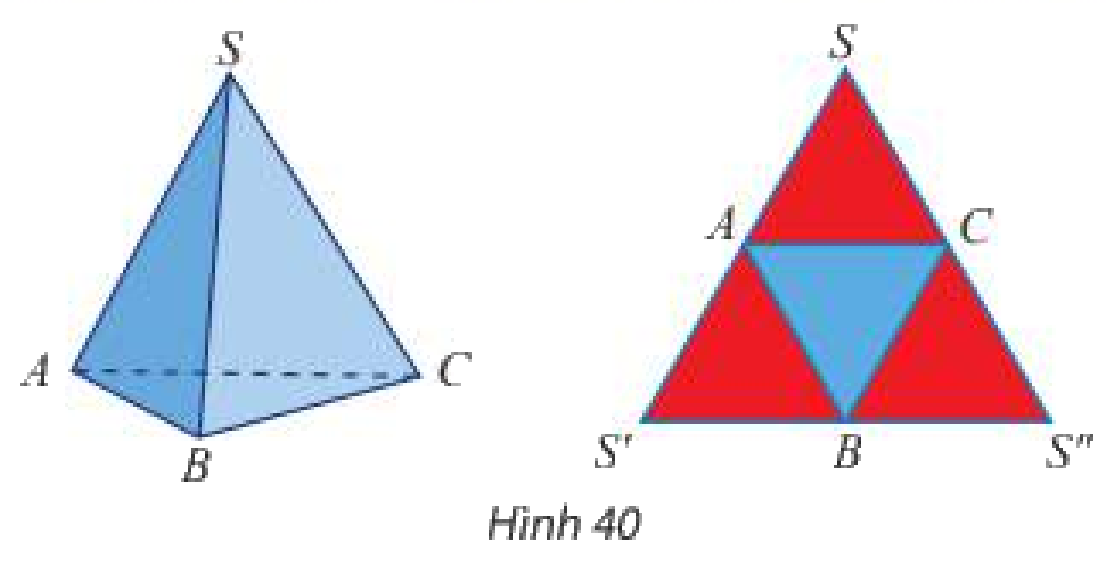
Nêu cách tạo lập tứ diện đều \(SABC\) từ tam giác đều \(SS'S''\) theo gợi ý ở Hình 40.

Phương pháp giải:
Để dựng được tứ diện đều, ta dựng một hình tứ diện có bốn mặt là các tam giác đều.
Lời giải chi tiết:
• Cách dựng:
Bước 1: Gọi \(A,B,C\) lần lượt là trung điểm của \(SS',S'S'',SS''\).
Bước 2: Gấp các đường \(AB,BC,AC\) sao cho các điểm \(S,S',S''\) trùng nhau.
Khi đó, ta được tứ diện đều \(SABC\).
• Chứng minh:
Vì \(A,B,C\) lần lượt là trung điểm của \(SS',S'S'',SS''\) nên theo tính chất đường trung bình của tam giác, ta có: \(SA = S'A = S'B = S''B = SC = S'C = AB = BC = AC = \frac{1}{2}SS'\).
Do vậy các tam giác \(SAC,S'AB,S''BC,ABC\) là các tam giác đều.
Vậy tứ diện \(SABC\) có các mặt \(SAC,SAB,SBC,ABC\) là các tam giác đều nên tứ diện \(SABC\) là tứ diện đều.
Giải mục 4 trang 96, 97, 98 SGK Toán 11 tập 1 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu
Chào mừng các em học sinh đến với bài viết hướng dẫn giải chi tiết các bài tập trong mục 4 trang 96, 97, 98 Sách Giáo Khoa Toán 11 tập 1, chương trình Chân trời sáng tạo. Tusach.vn tự hào là nguồn tài liệu học tập uy tín, cung cấp lời giải chính xác, dễ hiểu và phù hợp với mọi trình độ học sinh.
Tổng quan về mục 4 SGK Toán 11 tập 1 - Chân trời sáng tạo
Mục 4 của SGK Toán 11 tập 1 - Chân trời sáng tạo tập trung vào việc ôn tập và củng cố kiến thức về... (nêu rõ chủ đề chính của mục 4, ví dụ: hàm số bậc hai, phương trình bậc hai, bất phương trình bậc hai...). Các bài tập trong mục này giúp học sinh rèn luyện kỹ năng giải toán, áp dụng kiến thức vào thực tế và chuẩn bị cho các bài kiểm tra sắp tới.
Nội dung chi tiết lời giải các bài tập
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 4 trang 96, 97, 98 SGK Toán 11 tập 1 - Chân trời sáng tạo:
Bài 1: ...
Đề bài: ... (viết lại đề bài đầy đủ)
Lời giải: ... (giải chi tiết bài toán, kèm theo giải thích rõ ràng từng bước)
Bài 2: ...
Đề bài: ... (viết lại đề bài đầy đủ)
Lời giải: ... (giải chi tiết bài toán, kèm theo giải thích rõ ràng từng bước)
Bài 3: ...
Đề bài: ... (viết lại đề bài đầy đủ)
Lời giải: ... (giải chi tiết bài toán, kèm theo giải thích rõ ràng từng bước)
Các dạng bài tập thường gặp trong mục 4
- Dạng 1: ... (mô tả dạng bài tập và cách giải)
- Dạng 2: ... (mô tả dạng bài tập và cách giải)
- Dạng 3: ... (mô tả dạng bài tập và cách giải)
Mẹo giải nhanh các bài tập Toán 11
Để giải nhanh và chính xác các bài tập Toán 11, các em có thể tham khảo một số mẹo sau:
- ... (mẹo 1)
- ... (mẹo 2)
- ... (mẹo 3)
Luyện tập thêm
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, các em có thể làm thêm các bài tập sau:
- ... (liệt kê các bài tập luyện tập)
Kết luận
Hy vọng với bài viết này, các em học sinh đã nắm vững kiến thức và kỹ năng giải các bài tập trong mục 4 trang 96, 97, 98 SGK Toán 11 tập 1 - Chân trời sáng tạo. Tusach.vn luôn đồng hành cùng các em trên con đường chinh phục tri thức. Chúc các em học tập tốt!
Lưu ý: Đây chỉ là bản phác thảo. Cần điền đầy đủ nội dung đề bài, lời giải chi tiết và các thông tin liên quan để hoàn thiện bài viết.