Giải mục 5 trang 117, 118, 119 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 5 trang 117, 118, 119 SGK Toán 11 tập 1 - Chân trời sáng tạo
Chào mừng các em học sinh đến với lời giải chi tiết mục 5 trang 117, 118, 119 SGK Toán 11 tập 1, chương trình Chân trời sáng tạo. Bài viết này sẽ giúp các em hiểu rõ hơn về các khái niệm và phương pháp giải bài tập trong chương trình học.
tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp những tài liệu và lời giải chính xác, dễ hiểu nhất.
Hình dạng của các đô vật như hộp phân, lồng đèn, hộp quà, lăng kính có đặc điểm gì giống nhau?
Hoạt động 6
Hình dạng của các đô vật như hộp phân, lồng đèn, hộp quà, lăng kính có đặc điểm gì giống nhau?
Phương pháp giải:
Quan sát hình vẽ, tìm ra các đặc điểm chung.
Lời giải chi tiết:
Các hình trên đều có một cặp mặt phẳng đối diện song song với nhau.
Hoạt động 7
Cho hình lăng trụ \(ABCD.A'B'C'D'\) có đáy \(ABCD\) là hình bình hành. Chứng minh rằng:
a) Bốn mặt bên và mặt đáy còn lại của hình lăng trụ là các hình bình hành;
b) Các mặt \(AA'C'C\) và \(BB'D'D\)là hình bình hành
c) Bốn đoạn thẳng \(A'C,AC',B'D,BD\) có cùng trung điểm.
Phương pháp giải:
‒ Sử dụng định lí 3: Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) song song với nhau. Nếu \(\left( R \right)\) cắt \(\left( P \right)\) thì cắt \(\left( Q \right)\) và hai giao tuyến của chúng song song.
‒ Sử dụng tính chất của hình lăng trụ.
‒ Sử dụng tính chất của hình bình hành.
Lời giải chi tiết:

a) Vì \(ABCD.A'B'C'D'\) là hình lăng trụ nên có:
‒ Hai đáy \(ABCD\) và \(A'B'C'D'\) bằng nhau và là hình bình hành.
‒ Các mặt bên \(AA'B'B,AA'D'D,BB'C'C,CC'D'D\) là các hình bình hành.
b) Ta có:
\(\left. \begin{array}{l}\left( {ABC{\rm{D}}} \right)\parallel \left( {A'B'C'D'} \right)\\\left( {AA'C'C} \right) \cap \left( {ABC{\rm{D}}} \right) = AC\\\left( {AA'C'C} \right) \cap \left( {A'B'C'D'} \right) = A'C'\end{array} \right\} \Rightarrow AC\parallel A'C'\)
Mà \(AA'\) và \(CC'\) là các cạnh bên của hình lăng trụ nên \(AA'\parallel CC'\)
Vậy \(AA'C'C\) là hình bình hành.
\(\left. \begin{array}{l}\left( {ABC{\rm{D}}} \right)\parallel \left( {A'B'C'D'} \right)\\\left( {BB'D'D} \right) \cap \left( {ABC{\rm{D}}} \right) = B{\rm{D}}\\\left( {BB'D'D} \right) \cap \left( {A'B'C'D'} \right) = B'D'\end{array} \right\} \Rightarrow B{\rm{D}}\parallel B'D'\)
Mà \(BB'\) và \(DD'\) là các cạnh bên của hình lăng trụ nên \(BB'\parallel DD'\)
Vậy \(BB'D'D\) là hình bình hành.
c) Ta có:
\(\left. \begin{array}{l}\left( {ABC{\rm{D}}} \right)\parallel \left( {A'B'C'D'} \right)\\\left( {A'B'C{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right) = C{\rm{D}}\\\left( {A'B'C{\rm{D}}} \right) \cap \left( {A'B'C'D'} \right) = A'B'\end{array} \right\} \Rightarrow C{\rm{D}}\parallel A'B'\left( 1 \right)\)
\(ABC{\rm{D}}\) là hình bình hành nên \(AB = CD\)
\(AA'B'B\) là hình bình hành nên \(AB = A'B'\)
Vậy \(A'B' = CD\left( 2 \right)\)
Từ (1) và (2) suy ra \(A'B'C{\rm{D}}\) là hình bình hành
\( \Rightarrow A'C,B'D\) cắt nhau tại trung điểm của mỗi đường.
Chứng minh tương tự ta có:
+ \(ABC'D'\) là hình bình hành nên \(AC',B{\rm{D}}'\) cắt nhau tại trung điểm của mỗi đường
+ \(A'BCD'\) là hình bình hành nên \(A'C,B{\rm{D}}'\) cắt nhau tại trung điểm của mỗi đường
Do đó bốn đoạn thẳng \(A'C,AC',B'D,BD\) có cùng trung điểm.
Thực hành 4
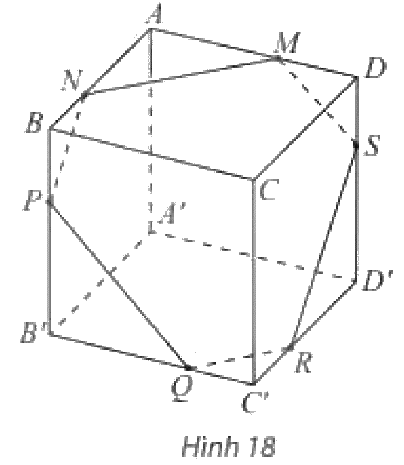
Cho hình hộp \(ABCD.A'B'C'D'\) và một mặt phẳng \(\left( \alpha \right)\) cắt các mặt của hình hộp theo các giao tuyến \(MN,NP,PQ{\rm{,}}QR,RS,SM\) như Hình 18. Chứng minh các cặp cạnh đối của lục giác \(MNPQRS\) song song với nhau.

Phương pháp giải:
Sử dụng định lí 3: Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) song song với nhau. Nếu \(\left( R \right)\) cắt \(\left( P \right)\) thì cắt \(\left( Q \right)\) và hai giao tuyến của chúng song song.
Lời giải chi tiết:
Ta có:
\(\left. \begin{array}{l}\left( {ABC{\rm{D}}} \right)\parallel \left( {A'B'C'D'} \right)\\\left( \alpha \right) \cap \left( {ABC{\rm{D}}} \right) = MN\\\left( \alpha \right) \cap \left( {A'B'C'D'} \right) = Q{\rm{R}}\end{array} \right\} \Rightarrow MN\parallel Q{\rm{R}}\)
\(\left. \begin{array}{l}\left( {AA'B'B} \right)\parallel \left( {CC'D'D} \right)\\\left( \alpha \right) \cap \left( {AA'B'B} \right) = NP\\\left( \alpha \right) \cap \left( {CC'D'D} \right) = R{\rm{S}}\end{array} \right\} \Rightarrow NP\parallel R{\rm{S}}\)
\(\left. \begin{array}{l}\left( {AA'D'D} \right)\parallel \left( {BB'C'C} \right)\\\left( \alpha \right) \cap \left( {AA'D'D} \right) = M{\rm{S}}\\\left( \alpha \right) \cap \left( {BB'C'C} \right) = PQ\end{array} \right\} \Rightarrow M{\rm{S}}\parallel PQ\)
Vận dụng 3
Tìm hình lăng trụ có thể lấy một mặt bất kì làm mặt đáy.
Phương pháp giải:
Sử dụng tính chất của hình lăng trụ, tìm các hình lăng trụ có các cặp mặt phẳng đối diện song song với nhau.
Lời giải chi tiết:
Hình lăng trụ có thể lấy một mặt bất kì làm mặt đáy là: Hình hộp, hình hộp chữ nhật, hình lập phương.
Giải mục 5 trang 117, 118, 119 SGK Toán 11 tập 1 - Chân trời sáng tạo: Tổng quan và Phương pháp giải
Mục 5 trong SGK Toán 11 tập 1 chương trình Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể, ví dụ như các phép biến hình, hàm số lượng giác, hoặc các bài toán về vectơ. Việc nắm vững kiến thức lý thuyết và phương pháp giải bài tập trong mục này là vô cùng quan trọng để các em có thể tự tin giải quyết các bài toán phức tạp hơn trong tương lai.
Nội dung chính của Mục 5
Để hiểu rõ hơn về Mục 5, chúng ta cần xem xét các nội dung chính sau:
- Lý thuyết trọng tâm: Tóm tắt các định nghĩa, tính chất, và công thức quan trọng liên quan đến chủ đề của Mục 5.
- Ví dụ minh họa: Phân tích các ví dụ điển hình để hiểu rõ cách áp dụng lý thuyết vào thực tế.
- Bài tập áp dụng: Luyện tập các bài tập từ dễ đến khó để củng cố kiến thức và kỹ năng.
Hướng dẫn giải chi tiết các bài tập trang 117, 118, 119
Dưới đây là hướng dẫn giải chi tiết các bài tập trong Mục 5, trang 117, 118, 119 SGK Toán 11 tập 1 - Chân trời sáng tạo:
Bài 1: (Trang 117)
Đề bài: (Giả sử đề bài là một bài toán cụ thể về vectơ)...
Lời giải: (Giải chi tiết bài toán, bao gồm các bước thực hiện, giải thích rõ ràng, và kết luận)...
Bài 2: (Trang 118)
Đề bài: (Giả sử đề bài là một bài toán về hàm số lượng giác)...
Lời giải: (Giải chi tiết bài toán, bao gồm các bước thực hiện, giải thích rõ ràng, và kết luận)...
Bài 3: (Trang 119)
Đề bài: (Giả sử đề bài là một bài toán về phép biến hình)...
Lời giải: (Giải chi tiết bài toán, bao gồm các bước thực hiện, giải thích rõ ràng, và kết luận)...
Mẹo giải nhanh và hiệu quả
Để giải các bài tập trong Mục 5 một cách nhanh chóng và hiệu quả, các em có thể tham khảo một số mẹo sau:
- Đọc kỹ đề bài: Xác định rõ yêu cầu của bài toán và các dữ kiện đã cho.
- Vẽ hình minh họa: Nếu có thể, hãy vẽ hình minh họa để giúp hình dung rõ hơn về bài toán.
- Sử dụng công thức và tính chất: Áp dụng các công thức và tính chất đã học để giải bài toán.
- Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Tài liệu tham khảo thêm
Ngoài SGK, các em có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức và kỹ năng:
- Sách bài tập Toán 11 tập 1 - Chân trời sáng tạo
- Các trang web học Toán trực tuyến uy tín
- Các video bài giảng Toán 11 trên YouTube
Hy vọng rằng với những hướng dẫn chi tiết và mẹo giải nhanh trên, các em sẽ tự tin chinh phục các bài tập trong Mục 5 trang 117, 118, 119 SGK Toán 11 tập 1 - Chân trời sáng tạo. Chúc các em học tập tốt!