Bài 6 trang 12 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Bài 6 trang 12 SGK Toán 11 tập 1 - Chân trời sáng tạo
Bài 6 trang 12 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Chân trời sáng tạo, tập trung vào việc luyện tập về các phép biến đổi lượng giác cơ bản. Bài tập này giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán lượng giác.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, cùng với phương pháp giải bài tập để giúp các em học sinh nắm vững kiến thức và tự tin làm bài.
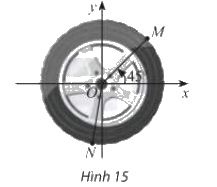
Trong Hình 15, mâm bánh xe ô tô được chia thành năm phần bằng nhau. Viết công thức số đo tổng quát của góc lượng giác (Ox; ON).
Đề bài
Trong Hình 15, mâm bánh xe ô tô được chia thành năm phần bằng nhau. Viết công thức số đo tổng quát của góc lượng giác (Ox; ON).
Phương pháp giải - Xem chi tiết
Sử dụng công thức số đo tổng quát của góc lượng giác.
Lời giải chi tiết
Vì mâm bánh xe ô tô được chia thành năm phần bằng nhau nên một phần có số đo là \(\frac{{{{360}^ \circ }}}{5} = {72^ \circ }\)
Ta có
\[\begin{array}{l}\left( {ON;{\rm{ }}OM} \right) = \left( {ON;{\rm{ }}Ox} \right) + \left( {Ox;{\rm{ }}OM} \right)\\\,\,\,\,\,\,\,{2.72^ \circ }\,\,\,\,\,\,\, = \,\left( {ON;{\rm{ }}Ox} \right)\, + \,\,\,\,\,\,\,{45^ \circ }\\ \Rightarrow \left( {ON;{\rm{ }}Ox} \right) = {99^ \circ }\end{array}\]
Công thức số đo tổng quát của góc lượng giác \[\left( {ON;{\rm{ }}Ox} \right) = {99^ \circ } + k{.360^ \circ }\,\,(k \in Z)\]
Bài 6 trang 12 SGK Toán 11 tập 1 - Chân trời sáng tạo: Giải chi tiết và phương pháp
Bài 6 trang 12 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh ôn luyện và củng cố kiến thức về các phép biến đổi lượng giác. Dưới đây là lời giải chi tiết và phương pháp giải bài tập này:
Nội dung bài tập
Bài tập yêu cầu chúng ta thực hiện các phép biến đổi lượng giác để rút gọn biểu thức hoặc chứng minh đẳng thức. Cụ thể, bài tập thường bao gồm các dạng sau:
- Rút gọn biểu thức lượng giác sử dụng các công thức lượng giác cơ bản.
- Chứng minh đẳng thức lượng giác bằng cách biến đổi một vế về vế còn lại.
- Tìm giá trị của biểu thức lượng giác khi biết giá trị của một góc.
Phương pháp giải
Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các công thức lượng giác cơ bản sau:
- Công thức cộng và hiệu lượng giác: sin(a ± b), cos(a ± b), tan(a ± b), cot(a ± b)
- Công thức nhân đôi: sin(2a), cos(2a), tan(2a), cot(2a)
- Công thức hạ bậc: sin2(a), cos2(a), tan2(a), cot2(a)
- Các công thức lượng giác khác: sin2(a) + cos2(a) = 1, tan(a) = sin(a)/cos(a), cot(a) = cos(a)/sin(a)
Ngoài ra, chúng ta cần chú ý đến việc sử dụng các kỹ năng biến đổi đại số để rút gọn biểu thức hoặc chứng minh đẳng thức.
Lời giải chi tiết
(Giả sử bài tập cụ thể là: Rút gọn biểu thức A = sin2(x) + cos2(x) + tan(x)cot(x))
Lời giải:
- Ta có: sin2(x) + cos2(x) = 1 (theo công thức lượng giác cơ bản)
- Ta có: tan(x)cot(x) = tan(x) * (1/tan(x)) = 1
- Vậy, A = 1 + 1 = 2
Ví dụ minh họa
Hãy xét bài tập sau: Chứng minh đẳng thức sin2(x) + cos2(x) = 1
Lời giải:
Ta có thể chứng minh đẳng thức này bằng cách sử dụng định nghĩa của sin và cos trong tam giác vuông. Giả sử tam giác ABC vuông tại A, với góc B = x. Khi đó:
- sin(x) = AC/BC
- cos(x) = AB/BC
Áp dụng định lý Pitago, ta có: AB2 + AC2 = BC2. Chia cả hai vế cho BC2, ta được:
(AB/BC)2 + (AC/BC)2 = 1
Hay cos2(x) + sin2(x) = 1. Vậy đẳng thức được chứng minh.
Bài tập luyện tập
Để củng cố kiến thức, các em có thể tự giải các bài tập sau:
- Rút gọn biểu thức: B = cos2(x) - sin2(x)
- Chứng minh đẳng thức: tan(x) + cot(x) = 1/sin(x)cos(x)
Kết luận
Bài 6 trang 12 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh nắm vững kiến thức về các phép biến đổi lượng giác. Bằng cách nắm vững các công thức lượng giác cơ bản và rèn luyện kỹ năng biến đổi đại số, các em có thể tự tin giải quyết các bài tập tương tự.