Giải mục 1 trang 52, 53 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 1 trang 52, 53 SGK Toán 11 tập 1 - Chân trời sáng tạo
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Toán 11 tập 1 Chân trời sáng tạo. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, vì vậy chúng tôi luôn cố gắng mang đến những giải pháp tốt nhất để giúp bạn học tập hiệu quả.
Bài viết này sẽ tập trung vào việc giải mục 1 trang 52, 53, giúp bạn hiểu rõ các khái niệm và phương pháp giải bài tập liên quan.
Tìm điểm giống nhau của các dãy số sau:
Hoạt động 1
Tìm điểm giống nhau của các dãy số sau:
a) 2; 5; 8; 11; 14 (xem Hình 1).
b) 2; 4; 6; 8.
c) 5; 10; 15; 20; 25.
d) ‒5; ‒2; 1; 4; 7; 10.
Phương pháp giải:
Xem hai số hạng liên tiếp của dãy có liên hệ gì.
Lời giải chi tiết:
Ta thấy:
a) Số sau hơn số liền trước 3 đơn vị.
b) Số sau hơn số liền trước 2 đơn vị.
c) Số sau hơn số liền trước 5 đơn vị.
d) Số sau hơn số liền trước 3 đơn vị.
Điểm giống nhau của các dãy số này là hai số hạng liền nhau hơn kém nhau một số không đổi.
Thực hành 1
Chứng minh mỗi dãy số sau là cấp số cộng. Xác định công sai của mỗi cấp số cộng đó.
a) 3; 7; 11; 15; 19; 23.
b) Dãy số \(\left( {{u_n}} \right)\) với \({u_n} = 9n - 9\).
c) Dãy số \(\left( {{v_n}} \right)\) với \({v_n} = an + b\), trong đó \(a\) và \(b\) là các hằng số.
Phương pháp giải:
Biến đổi, đưa \({u_{n + 1}} = {u_n} + d\), khi đó dãy số là cấp số cộng có công sai \(d\).
Lời giải chi tiết:
a) Dãy số: 3; 7; 11; 15; 19; 23 là cấp số cộng có công sai \(d = 4\).
b) Ta có: \({u_{n + 1}} = 9\left( {n + 1} \right) - 9 = 9n + 9 - 9 = \left( {9n - 9} \right) + 9 = {u_n} + 9\).
Vậy dãy số \(\left( {{u_n}} \right)\) là cấp số cộng có công sai \({\rm{d}} = 9\).
c) Ta có: \({v_{n + 1}} = a\left( {n + 1} \right) + b = an + a + b = \left( {an + b} \right) + a = {v_n} + a\).
Vậy dãy số \(\left( {{v_n}} \right)\) là cấp số cộng có công sai \({\rm{d}} = a\).
Thực hành 2
Số đo ba góc của một tam giác vuông lập thành cấp số cộng. Tìm số đo ba góc đó.
Phương pháp giải:
Dựa vào tính chất:
‒ Tam giác vuông có một góc bằng \({90^ \circ }\).
‒ Tổng ba góc trong tam giác bằng \({180^ \circ }\).
Lời giải chi tiết:
Do tam giác đó là tam giác vuông nên có một góc bằng \({90^ \circ }\).
Giả sử hai góc còn lại của tam giác có số đo lần lượt là \(a,b\left( {{0^ \circ } < a,b < {{90}^ \circ }} \right)\).
Vì tổng ba góc trong tam giác bằng \({180^ \circ }\) nên ta có: \(a + b + {90^ \circ } = {180^ \circ } \Leftrightarrow a + b = {90^ \circ }\)(1).
Vì số đo ba góc trong tam giác lập thành cấp số cộng nên ta có:
\(b = \frac{{a + {{90}^ \circ }}}{2} \Leftrightarrow 2b = a + {90^ \circ } \Leftrightarrow - a + 2b = {90^ \circ }\) (2)
Từ (1) và (2) ta có hệ phương trình sau:
\(\left\{ \begin{array}{l}a + b = {90^ \circ }\\ - a + 2b = {90^ \circ }\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = {30^ \circ }\\b = {60^ \circ }\end{array} \right.\)
Vậy số đo ba góc của tam giác vuông đó lần lượt là: \({30^ \circ };{60^ \circ };{90^ \circ }\).
Vận dụng 1
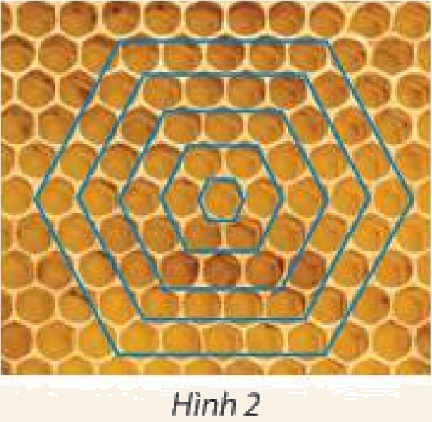
Mặt cắt của một tổ ong có hình lưới tạo bởi các ô hình lục giác đều. Từ một ô đầu tiên, bước thứ nhất, các ong thợ tạo ra vòng 1 gồm 6 ô lục giác; bước thứ hai, các ong thợ sẽ tạo ra vòng 2 có 12 ô bao quanh vòng 1; bước thứ ba, các ong thợ sẽ tạo ra 18 ô bao quanh vòng 2; cứ thế tiếp tục (Hình 2). Số ô trên các vòng theo thứ tự có tạo thành cấp số cộng không? Nếu có, tìm công sai của cấp số cộng này.

Phương pháp giải:
Biến đổi, đưa \({u_{n + 1}} = {u_n} + d\), khi đó dãy số là cấp số cộng có công sai \(d\).
Lời giải chi tiết:
Ta có: Dãy số chỉ số ô trên các vòng là: \({u_1} = 6;{u_2} = 12;{u_3} = 18;...\)
Ta thấy: \({u_{n + 1}} = {u_n} + 6\)
Vậy ô trên các vòng theo thứ tự tạo thành cấp số cộng có công sai \({\rm{d}} = 6\).
Giải mục 1 trang 52, 53 SGK Toán 11 tập 1 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu
Mục 1 của chương trình Toán 11 tập 1 Chân trời sáng tạo thường xoay quanh các khái niệm cơ bản về hàm số, bao gồm định nghĩa, các loại hàm số, và cách xác định tập xác định của hàm số. Việc nắm vững kiến thức này là nền tảng quan trọng để giải quyết các bài tập phức tạp hơn trong chương trình học.
Nội dung chính của Mục 1 trang 52, 53
Mục 1 thường bao gồm các nội dung sau:
- Định nghĩa hàm số: Hàm số là một quy tắc tương ứng giữa hai tập hợp, tập xác định và tập giá trị.
- Các loại hàm số: Hàm số chẵn, hàm số lẻ, hàm số đồng biến, hàm số nghịch biến.
- Tập xác định của hàm số: Tập hợp tất cả các giá trị của x sao cho hàm số f(x) có nghĩa.
- Cách xác định tập xác định: Xác định các điều kiện để hàm số có nghĩa (ví dụ: mẫu số khác 0, căn thức không âm, logarit có cơ số lớn hơn 0 và khác 1).
Giải chi tiết các bài tập trong Mục 1 trang 52, 53
Dưới đây là giải chi tiết một số bài tập thường gặp trong Mục 1 trang 52, 53 SGK Toán 11 tập 1 Chân trời sáng tạo:
Bài 1: Xác định tập xác định của hàm số
Ví dụ: Cho hàm số f(x) = √(x - 2). Tập xác định của hàm số là:
x - 2 ≥ 0 ⇔ x ≥ 2
Vậy tập xác định của hàm số là D = [2; +∞).
Bài 2: Xét tính chẵn, lẻ của hàm số
Ví dụ: Cho hàm số f(x) = x2. Để xét tính chẵn, lẻ, ta tính f(-x):
f(-x) = (-x)2 = x2 = f(x)
Vì f(-x) = f(x) với mọi x thuộc tập xác định, nên hàm số f(x) = x2 là hàm số chẵn.
Bài 3: Tìm khoảng đồng biến, nghịch biến của hàm số
Ví dụ: Cho hàm số f(x) = 2x + 1. Hàm số là hàm số bậc nhất với hệ số a = 2 > 0, nên hàm số đồng biến trên R.
Mẹo giải bài tập hiệu quả
- Nắm vững định nghĩa: Hiểu rõ các khái niệm cơ bản là chìa khóa để giải quyết mọi bài tập.
- Phân tích kỹ đề bài: Đọc kỹ đề bài, xác định rõ yêu cầu và các điều kiện ràng buộc.
- Sử dụng các công thức và tính chất: Áp dụng các công thức và tính chất đã học để đơn giản hóa bài toán.
- Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Tài liệu tham khảo hữu ích
Ngoài sách giáo khoa, bạn có thể tham khảo thêm các tài liệu sau:
- Sách bài tập Toán 11 tập 1 Chân trời sáng tạo
- Các trang web học toán trực tuyến uy tín
- Các video hướng dẫn giải bài tập trên YouTube
Kết luận
Hy vọng với hướng dẫn chi tiết này, bạn đã có thể tự tin giải các bài tập trong Mục 1 trang 52, 53 SGK Toán 11 tập 1 Chân trời sáng tạo. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình. Chúc bạn học tập tốt!