Bài 6 trang 33 Toán 11 Tập 1 - Chân trời sáng tạo

Bài 6 trang 33 SGK Toán 11 tập 1 - Chân trời sáng tạo

Bài 6 trang 33 SGK Toán 11 Tập 1 - Chân trời sáng tạo

Bài 6 trang 33 SGK Toán 11 Tập 1 thuộc chương trình học Toán 11 Chân trời sáng tạo, tập trung vào việc giải quyết các bài toán liên quan đến phép biến hóa lượng giác. Bài tập này giúp học sinh củng cố kiến thức về các công thức lượng giác cơ bản và rèn luyện kỹ năng giải toán.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

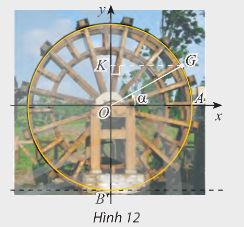
Khoảng cách từ tâm một guồng nước đến mặt nước và bán kính của guồng đều bằng 3m.

Đề bài

Khoảng cách từ tâm một guồng nước đến mặt nước và bán kính của guồng đều bằng 3m. Xét gàu G của guồng. Ban đầu gàu G nằm ở vị trí A (Hình 12)

a) Viết hàm số h biểu diễn chiều cao (tính bằng mét) của gàu G so với mặt nước theo góc \(\alpha = (OA,OG)\)

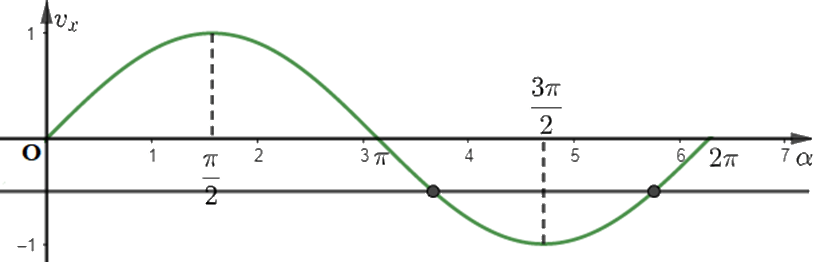
b) Guồng nước quay hết mỗi vòng trong 30 giây. Dựa vào đồ thị của hàm số sin, hãy cho biết ở các thời điểm t nào trong 1 phút đầu, khoảng cách của gàu đến mặt nước bằng 1,5m.

Bài 6 trang 33 SGK Toán 11 tập 1 - Chân trời sáng tạo 1

Phương pháp giải - Xem chi tiết Bài 6 trang 33 SGK Toán 11 tập 1 - Chân trời sáng tạo 2

Dựa vào hình vẽ và sử dụng đồ thị hàm số sin để trả lời.

Lời giải chi tiết

a) Điểm G là điểm biểu diễn cho góc lượng giác có số đo \(\alpha \). Khi đó tọa độ điểm \(G\left( {3cos\alpha ;{\rm{ }}3sin\alpha } \right)\).

Chiều cao của gàu ở vị trí G đến mặt nước là: \(3{\rm{ }} + {\rm{ }}3sin\alpha \) (m).

b) b) Khoảng cách của gàu đến mặt nước bằng 1,5m khi \(3 + 3sin\alpha = 1,5 \Leftrightarrow sin\alpha {\rm{ }} = \frac{{ - 1}}{2}\)

\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\alpha = \frac{{ - \pi }}{6} + k2\pi }\\{\alpha = \frac{{7\pi }}{6} + k2\pi }\end{array}} \right.\)

Một vòng quay là 30 giây và t nằm trong khoảng từ 0 đến 1 phút do đó t ∈ [0; 2π].

Guồng quay mỗi vòng trong 30 giây nên 1 phút guồng quay được 2 vòng, tương ứng với \(4\pi \). Vậy khi gàu cách mặt nước 1,5m thì \(\alpha = \frac{{7\pi }}{6},\alpha = \frac{{19\pi }}{6},\alpha = \frac{{11\pi }}{6},\alpha = \frac{{23\pi }}{6}.\)

Guồng quay 1 vòng tương đương với góc \(2\pi \) hết 30 giây nên để quay hết \(\frac{\pi }{6}\) vòng mất 2,5 giây.

Guồng quay 1 góc \(\alpha = \frac{{7\pi }}{6}\) hết 17,5 giây.

Guồng quay 1 góc \(\alpha = \frac{{19\pi }}{6}\) hết 47,5 giây.

Guồng quay 1 góc \(\alpha = \frac{{11\pi }}{6}\) hết 27,5 giây.

Guồng quay 1 góc \(\alpha = \frac{{23\pi }}{6}\) hết 57,5 giây.

Vậy, ở thời điểm t bằng 17,5 giây, 27,5 giây, 47,5 giây và 57,5 giây, gàu ở cách mặt nước 1,5m.

\(\)

Bài 6 trang 33 SGK Toán 11 tập 1 - Chân trời sáng tạo 3

Bài 6 trang 33 SGK Toán 11 Tập 1 - Chân trời sáng tạo: Giải chi tiết và hướng dẫn

Bài 6 trang 33 SGK Toán 11 Tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh rèn luyện kỹ năng áp dụng các công thức lượng giác để giải quyết các bài toán thực tế. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:

Nội dung bài tập

Bài 6 yêu cầu học sinh thực hiện các phép biến đổi lượng giác để rút gọn biểu thức hoặc chứng minh đẳng thức. Các dạng bài tập thường gặp bao gồm:

Rút gọn biểu thức lượng giác sử dụng các công thức cộng, trừ, nhân, chia góc.
Chứng minh đẳng thức lượng giác bằng cách biến đổi một vế về vế còn lại.
Giải phương trình lượng giác cơ bản.

Lời giải chi tiết

Để giải bài 6 trang 33, chúng ta cần nắm vững các công thức lượng giác cơ bản sau:

sin(a + b) = sin(a)cos(b) + cos(a)sin(b)
cos(a + b) = cos(a)cos(b) - sin(a)sin(b)
tan(a + b) = (tan(a) + tan(b)) / (1 - tan(a)tan(b))
sin²(x) + cos²(x) = 1

Ví dụ: Giả sử bài tập yêu cầu rút gọn biểu thức A = sin(x + π/3). Ta có thể sử dụng công thức sin(a + b) để biến đổi như sau:

A = sin(x + π/3) = sin(x)cos(π/3) + cos(x)sin(π/3) = sin(x) * (1/2) + cos(x) * (√3/2)

Mẹo giải nhanh

Để giải nhanh các bài tập lượng giác, bạn nên:

Nắm vững các công thức lượng giác cơ bản.
Phân tích bài toán để xác định công thức phù hợp.
Biến đổi biểu thức một cách cẩn thận và chính xác.
Kiểm tra lại kết quả sau khi giải xong.

Bài tập tương tự

Để củng cố kiến thức, bạn có thể luyện tập thêm các bài tập tương tự sau:

Rút gọn biểu thức B = cos(x - π/4)
Chứng minh đẳng thức sin²(x) + cos²(x) = 1
Giải phương trình sin(x) = 1/2

Tài liệu tham khảo

Ngoài SGK Toán 11 Tập 1 - Chân trời sáng tạo, bạn có thể tham khảo thêm các tài liệu sau:

Sách bài tập Toán 11
Các trang web học Toán online uy tín như tusach.vn
Các video hướng dẫn giải Toán 11 trên YouTube

Kết luận: Bài 6 trang 33 SGK Toán 11 Tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán lượng giác. Bằng cách nắm vững các công thức và áp dụng các mẹo giải nhanh, bạn có thể tự tin giải quyết các bài tập tương tự.

Công thức	Mô tả
sin(a + b)	Công thức cộng sin
cos(a + b)	Công thức cộng cos