Lý thuyết Đường thẳng và mặt phẳng song song - SGK Toán 11 Chân trời sáng tạo
Tổng quan nội dung
Lý thuyết Đường thẳng và Mặt phẳng song song - Nền tảng Toán 11
Trong chương trình Toán 11, phần Lý thuyết Đường thẳng và Mặt phẳng song song đóng vai trò quan trọng trong việc xây dựng nền tảng kiến thức về Hình học không gian.
Tusach.vn cung cấp tài liệu học tập đầy đủ, chi tiết, giúp bạn nắm vững các khái niệm, định lý và phương pháp giải bài tập liên quan đến chủ đề này.
1. Đường thẳng song song với mặt phẳng
1. Đường thẳng song song với mặt phẳng
- Nếu a và \(\left( P \right)\) có một điểm chung duy nhất thì ta nói a và \(\left( P \right)\) cắt nhau tại A. Kí hiệu \(a \cap \left( P \right) = A\) hay \(a \cap \left( P \right) = \left\{ A \right\}\).
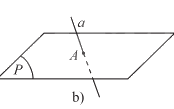
- Nếu a và \(\left( P \right)\) có từ 2 điểm chung phân biệt trở lên thì ta nói a nằm trong \(\left( P \right)\) hay \(\left( P \right)\) chứa a. Kí hiệu \(a \subset \left( P \right)\) hay \(\left( P \right) \supset a\).
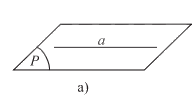
- Nếu a và \(\left( P \right)\) không có điểm chung thì ta nói a song song với \(\left( P \right)\) hay \(\left( P \right)\)song song với a. Kí hiệu là \(a//\left( P \right)\) hay \(\left( P \right)//a\).
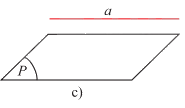
*Đường thẳng a song song với mặt phẳng (P) nếu chúng không có điểm chung.
2. Điều kiện để một đường thẳng song song với một mặt phẳng
- Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng b nào đó nằm trong (P) thì ta nói \(a//\left( P \right)\).
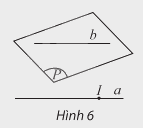
3. Tính chất cơ bản của đường thẳng và mặt phẳng song song
Cho đường thẳng a song song với mặt phẳng (P). Nếu mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b thì a // b.
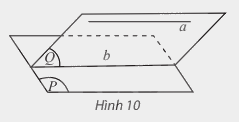
* Hệ quả:
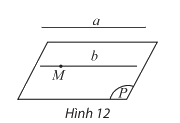
- Cho đường thẳng a song song với mặt phẳng (P). Nếu qua điểm M thuộc (P) ta vẽ đường thẳng b song song với a thì b phải nằm trong (P).
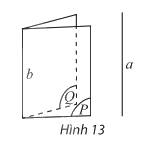
- Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.
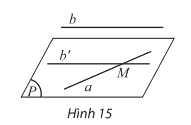
* Mặt phẳng đi qua một trong hai đường thẳng chéo nhau và song song vơi đường thẳng còn lại
- Nếu a và b là hai đường thẳng chéo nhau thì qua a, có một và chỉ một mặt phẳng song song với b.
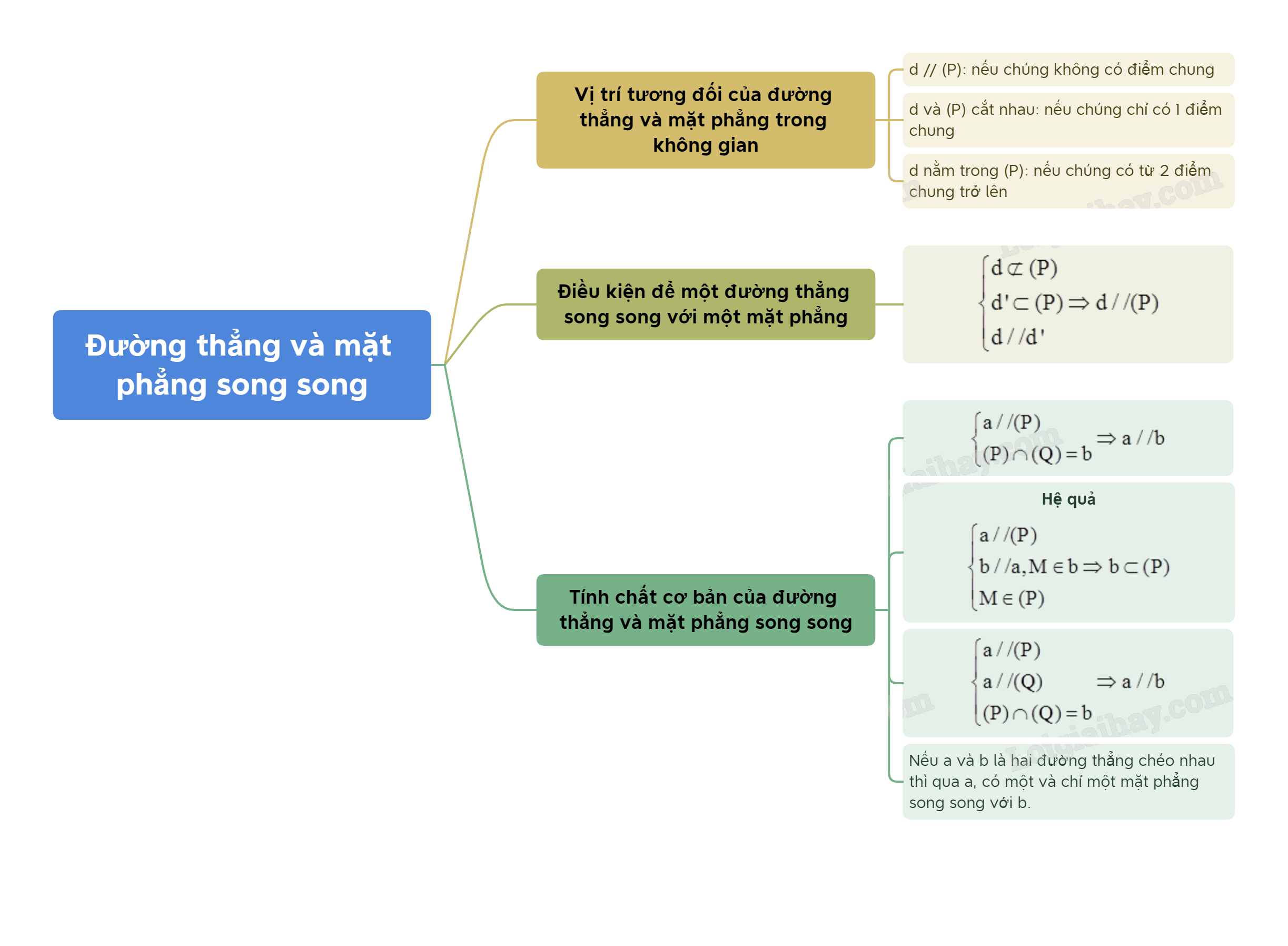
Lý Thuyết Đường Thẳng và Mặt Phẳng Song Song - SGK Toán 11 Chân Trời Sáng Tạo
Chương trình Toán 11 Chân Trời Sáng Tạo đi sâu vào các khái niệm cơ bản của Hình học không gian, trong đó, lý thuyết về đường thẳng và mặt phẳng song song là một phần không thể thiếu. Việc nắm vững kiến thức này là nền tảng để giải quyết các bài toán phức tạp hơn trong các chương tiếp theo.
1. Khái Niệm Cơ Bản
Để hiểu rõ về đường thẳng và mặt phẳng song song, chúng ta cần nắm vững các khái niệm sau:
- Đường thẳng song song: Hai đường thẳng được gọi là song song khi chúng không có điểm chung và nằm trong cùng một mặt phẳng.
- Mặt phẳng song song: Hai mặt phẳng được gọi là song song khi chúng không có điểm chung.
- Đường thẳng song song với mặt phẳng: Một đường thẳng được gọi là song song với một mặt phẳng khi nó không có điểm chung với mặt phẳng đó.
2. Các Điều Kiện Nhận Biết Đường Thẳng và Mặt Phẳng Song Song
Có nhiều cách để nhận biết đường thẳng và mặt phẳng song song. Dưới đây là một số điều kiện quan trọng:
- Hai đường thẳng song song khi:
- Chúng cùng song song với một đường thẳng thứ ba.
- Chúng cùng vuông góc với một đường thẳng thứ ba.
- Hai mặt phẳng song song khi:
- Chúng cùng song song với một đường thẳng thứ ba.
- Chúng cùng vuông góc với một đường thẳng thứ ba.
- Chúng chứa hai đường thẳng song song.
- Đường thẳng song song với mặt phẳng khi:
- Đường thẳng đó song song với một đường thẳng nằm trong mặt phẳng.
3. Tính Chất Quan Hệ Song Song
Các tính chất quan hệ song song đóng vai trò quan trọng trong việc chứng minh và giải quyết các bài toán hình học. Một số tính chất quan trọng bao gồm:
- Nếu một đường thẳng song song với một mặt phẳng thì mọi đường thẳng nằm trong mặt phẳng đó và song song với đường thẳng đã cho đều song song với mặt phẳng đó.
- Nếu hai mặt phẳng song song thì mọi đường thẳng nằm trong mặt phẳng này và song song với một đường thẳng nằm trong mặt phẳng kia đều song song với nhau.
4. Bài Tập Ví Dụ Minh Họa
Bài tập 1: Cho hình chóp S.ABCD. Gọi M là trung điểm của cạnh CD. Chứng minh rằng đường thẳng SM song song với mặt phẳng (ABD).
Hướng dẫn: Sử dụng tính chất đường thẳng song song với mặt phẳng khi đường thẳng đó song song với một đường thẳng nằm trong mặt phẳng.
Bài tập 2: Cho hai mặt phẳng (P) và (Q) song song với nhau. Trên (P) có hai điểm A và B. Trên (Q) có hai điểm C và D. Chứng minh rằng AB song song với CD.
Hướng dẫn: Sử dụng tính chất hai mặt phẳng song song chứa hai đường thẳng song song.
5. Luyện Tập và Củng Cố Kiến Thức
Để nắm vững lý thuyết và rèn luyện kỹ năng giải bài tập, bạn nên:
- Đọc kỹ SGK Toán 11 Chân Trời Sáng Tạo.
- Giải các bài tập trong SGK và sách bài tập.
- Tìm kiếm các tài liệu tham khảo trên internet.
- Luyện tập thường xuyên để củng cố kiến thức.
6. Tài Nguyên Hỗ Trợ Học Tập tại tusach.vn
Tusach.vn cung cấp đầy đủ các tài liệu hỗ trợ học tập, bao gồm:
- Bài giảng chi tiết
- Bài tập trắc nghiệm
- Bài tập tự luận
- Đáp án và lời giải chi tiết
Hãy truy cập tusach.vn ngay hôm nay để học tập hiệu quả và đạt kết quả cao trong môn Toán 11!