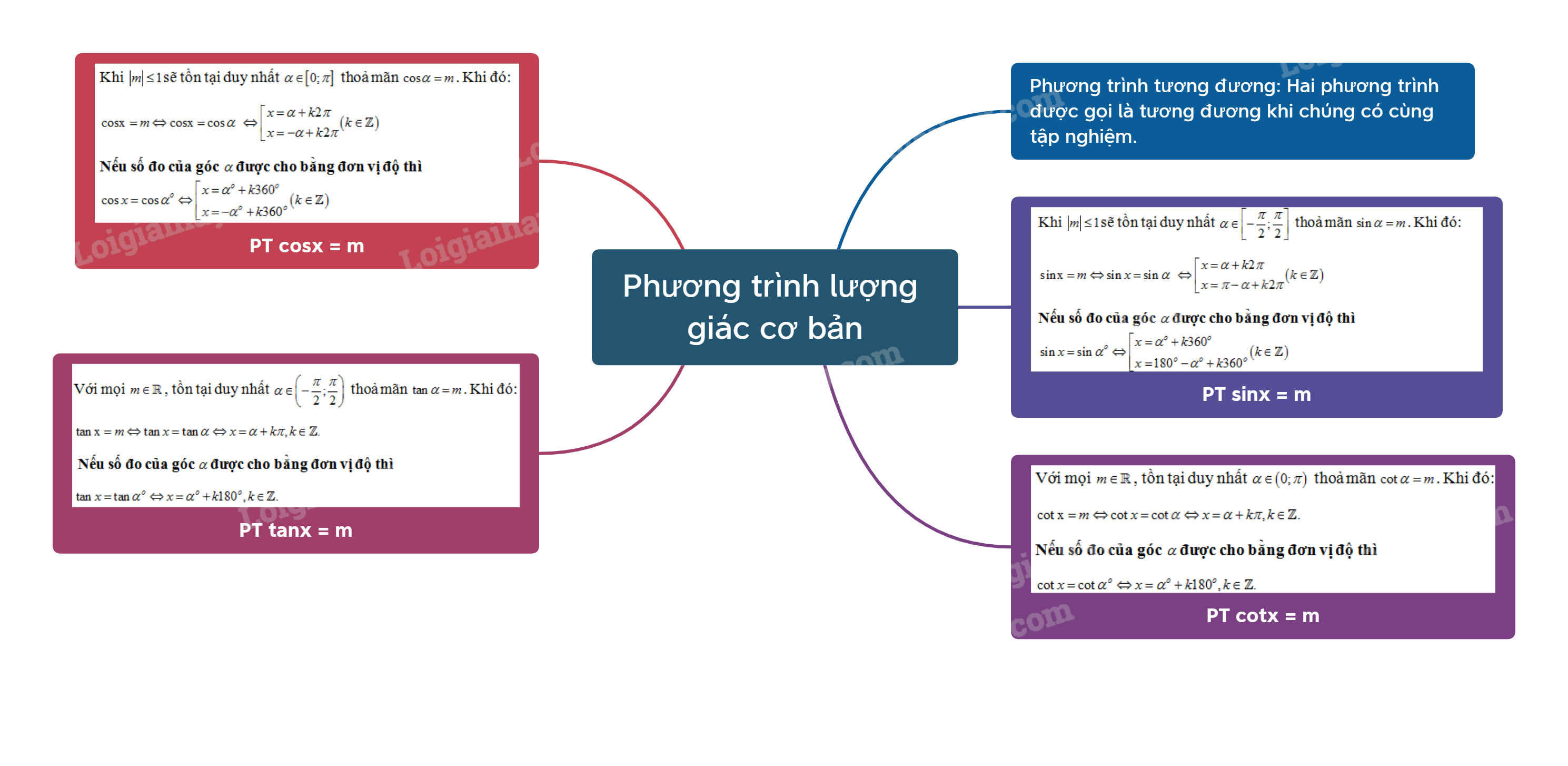
1. Khái niệm phương trình tương đương
- Hai phương trình (cùng ẩn) được gọi là tương đương khi chúng có cùng tập nghiệm.
- Nếu phương trình f(x) =0 tương đương với phương trình g(x) =0 thì ta viết \(f(x) = 0 \Leftrightarrow g(x) = 0\)
*Chú ý: Hai phương trình vô nghiệm là hai phương trình tương đương.
- Các phép biến đổi tương đương:
+ Cộng hay trừ hai vế với cùng một số hoặc cùng một biểu thức.
+ Nhân hoặc chia 2 vế với cùng một số khác 0 hoặc với cùng một biểu thức luôn có giá trị khác 0.
2. Phương trình \({\mathop{\rm s}\nolimits} {\rm{inx}} = m\)
Phương trình sinx=m có nghiệm khi và chỉ khi \(\left| m \right| \le 1\).
Khi \(\left| m \right| \le 1\)sẽ tồn tại duy nhất \(\alpha \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) thoả mãn \(\sin \alpha = m\). Khi đó:
\({\mathop{\rm s}\nolimits} {\rm{inx}} = m \Leftrightarrow \sin x = \sin \alpha \) \( \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
* Chú ý:
a, Nếu số đo của góc \(\alpha \)được cho bằng đơn vị độ thì \(\sin x = \sin {\alpha ^o} \Leftrightarrow \left[ \begin{array}{l}x = {\alpha ^o} + k{360^o}\\x = {180^o} - {\alpha ^o} + k{360^o}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
b,Một số trường hợp đặc biệt
\(\begin{array}{l}\sin x = 0 \Leftrightarrow x = k\pi ,k \in \mathbb{Z}.\\\sin x = 1 \Leftrightarrow x = \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}.\\\sin x = - 1 \Leftrightarrow x = - \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}.\end{array}\)
3. Phương trình \({\rm{cosx}} = m\)
Phương trình \({\rm{cosx}} = m\) có nghiệm khi và chỉ khi \(\left| m \right| \le 1\).
Khi \(\left| m \right| \le 1\) sẽ tồn tại duy nhất \(\alpha \in \left[ {0;\pi } \right]\) thoả mãn \({\rm{cos}}\alpha = m\). Khi đó:
\({\rm{cosx}} = m \Leftrightarrow {\rm{cosx}} = {\rm{cos}}\alpha \) \( \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = - \alpha + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
* Chú ý:
a, Nếu số đo của góc \(\alpha \)được cho bằng đơn vị độ thì \(\cos x = \cos {\alpha ^o} \Leftrightarrow \left[ \begin{array}{l}x = {\alpha ^o} + k{360^o}\\x = - {\alpha ^o} + k{360^o}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
b, Một số trường hợp đặc biệt
\(\begin{array}{l}{\rm{cos}}x = 0 \Leftrightarrow x = \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}.\\{\rm{cos}}x = 1 \Leftrightarrow x = k2\pi ,k \in \mathbb{Z}.\\{\rm{cos}}x = - 1 \Leftrightarrow x = \pi + k2\pi ,k \in \mathbb{Z}.\end{array}\)
4. Phương trình \(\tan x = m\)
Phương trình \(\tan x = m\)có nghiệm với mọi m.
Với mọi \(m \in \mathbb{R}\), tồn tại duy nhất \(\alpha \in \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) thoả mãn \(\tan \alpha = m\). Khi đó:
\(\tan {\rm{x}} = m \Leftrightarrow \tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi ,k \in \mathbb{Z}.\)
*Chú ý: Nếu số đo của góc \(\alpha \)được cho bằng đơn vị độ thì
\(\tan x = \tan {\alpha ^o} \Leftrightarrow x = {\alpha ^o} + k{180^o},k \in \mathbb{Z}.\)
5. Phương trình \(\cot x = m\)
Phương trình \(\cot x = m\)có nghiệm với mọi m.
Với mọi \(m \in \mathbb{R}\), tồn tại duy nhất \(\alpha \in \left( {0;\pi } \right)\) thoả mãn \(\cot \alpha = m\). Khi đó:
\(\cot {\rm{x}} = m \Leftrightarrow \cot x = \cot \alpha \Leftrightarrow x = \alpha + k\pi ,k \in \mathbb{Z}.\)
*Chú ý: Nếu số đo của góc \(\alpha \)được cho bằng đơn vị độ thì
\(\cot x = \cot {\alpha ^o} \Leftrightarrow x = {\alpha ^o} + k{180^o},k \in \mathbb{Z}.\)
6. Sử dụng máy tính cầm tay tìm góc khi biết giá trị lượng giác của nó
Bước 1. Chọn đơn vị đo góc (độ hoặc radian).
Muốn tìm số đo độ, ta ấn: SHIFT \( \to \)MODE \( \to \)3 (CASIO FX570VN).
Muốn tìm số đo radian, ta ấn: SHIFT \( \to \)MODE \( \to \)4 (CASIO FX570VN).
Bước 2. Tìm số đo góc.
Khi biết SIN, COS, TANG của góc \(\alpha \)ta cần tìm bằng m, ta lần lượt ấn các phím SHIFT và một trong các phím SIN, COS, TANG rồi nhập giá trị lượng giác m và cuối cùng ấn phím “BẰNG =”. Lúc này trên màn hình cho kết quả là số đo của góc \(\alpha \)
