Lý Thuyết Hai Đường Thẳng Vuông Góc - Toán 11 Cánh Diều

Lý thuyết Hai đường thẳng vuông góc - Toán 11 Cánh diều

Lý thuyết Hai Đường Thẳng Vuông Góc - Toán 11 Cánh Diều

Trong chương trình Toán 11, kiến thức về đường thẳng và mặt phẳng đóng vai trò quan trọng. Đặc biệt, lý thuyết về hai đường thẳng vuông góc là nền tảng để giải quyết nhiều bài toán hình học không gian.

Bài viết này của tusach.vn sẽ cung cấp một cách đầy đủ và dễ hiểu nhất về lý thuyết hai đường thẳng vuông góc, bao gồm định nghĩa, điều kiện, tính chất và các ứng dụng thực tế.

1. Góc giữa hai đường thẳng trong không gian Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm O và lần lượt song song (hoặc trùng) với a và b, kí hiệu (a, b) hoặc \(\widehat {(a,b)}\).

1. Góc giữa hai đường thẳng trong không gian

Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm O và lần lượt song song (hoặc trùng) với a và b, kí hiệu (a, b) hoặc \(\widehat {(a,b)}\).

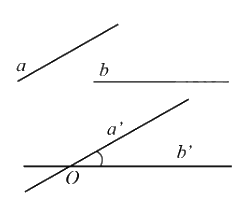
Lý thuyết Hai đường thẳng vuông góc - Toán 11 Cánh diều 1

Nhận xét:

- Góc giữa hai đường thẳng a, b không phụ thuộc vào vị trí điểm O. Thông thường, khi tìm góc giữa hai đường thẳng a, b, ta chọn O thuộc a hoặc O thuộc b.

- Góc giữa hai đường thẳng a, b bằng góc giữa hai đường thẳng b, a, tức là (a, b) = (b, a).

- Góc giữa hai đường thẳng không vượt quá \({90^0}\).

- Nếu a // b thì (a, c) = (b, c) với mọi đường thẳng c trong không gian.

2. Hai đường thẳng vuông góc trong không gian

Hai đường thẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng \({90^0}\).

Khi hai đường thẳng a và b vuông góc với nhau, ta kí hiệu \(a \bot b\).

Nhận xét: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại.

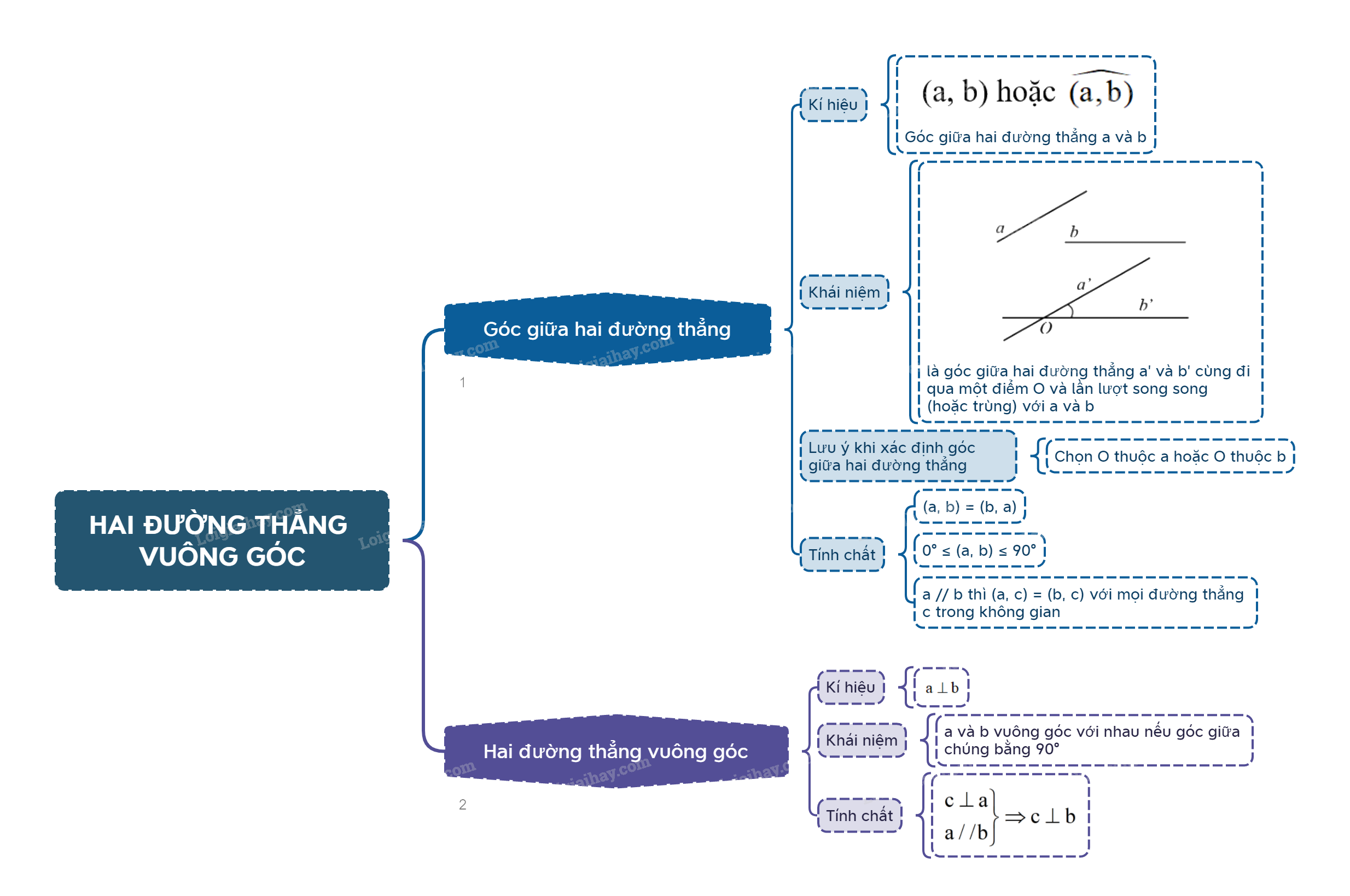
Lý thuyết Hai đường thẳng vuông góc - Toán 11 Cánh diều 2

Lý Thuyết Hai Đường Thẳng Vuông Góc - Toán 11 Cánh Diều: Giải Thích Chi Tiết và Bài Tập Minh Họa

Chào mừng các em học sinh đến với bài học về lý thuyết hai đường thẳng vuông góc trong chương trình Toán 11 Cánh Diều. Đây là một phần kiến thức quan trọng, giúp các em hiểu sâu hơn về mối quan hệ giữa các đường thẳng trong không gian và ứng dụng vào giải quyết các bài toán hình học.

1. Định Nghĩa Hai Đường Thẳng Vuông Góc

Hai đường thẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng 90°. Trong không gian, để xác định hai đường thẳng vuông góc, ta thường dựa vào vectơ chỉ phương của chúng.

2. Điều Kiện Hai Đường Thẳng Vuông Góc

Cho hai đường thẳng d₁ và d₂ lần lượt có vectơ chỉ phương u₁ và u₂. Hai đường thẳng d₁ và d₂ vuông góc với nhau khi và chỉ khi tích vô hướng của hai vectơ chỉ phương bằng 0:

u₁ ⋅ u₂ = 0

3. Tính Chất của Hai Đường Thẳng Vuông Góc

Nếu hai đường thẳng vuông góc với nhau, thì tích vô hướng của các vectơ chỉ phương của chúng bằng 0.
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song, thì nó cũng vuông góc với đường thẳng còn lại.

4. Ứng Dụng của Lý Thuyết Hai Đường Thẳng Vuông Góc

Lý thuyết này được ứng dụng rộng rãi trong việc giải các bài toán liên quan đến:

Xác định góc giữa hai đường thẳng.
Tìm điều kiện để hai đường thẳng vuông góc.
Tính khoảng cách từ một điểm đến một đường thẳng.
Giải các bài toán hình học không gian.

5. Bài Tập Minh Họa

Bài tập 1: Cho hai đường thẳng d₁: x - 2y + 3 = 0 và d₂: 2x + y - 1 = 0. Chứng minh rằng hai đường thẳng này vuông góc với nhau.

Giải:

Tìm vectơ chỉ phương của d₁: u₁ = (2, 1)
Tìm vectơ chỉ phương của d₂: u₂ = (-1, 2)
Tính tích vô hướng của u₁ và u₂: u₁ ⋅ u₂ = (2)(-1) + (1)(2) = 0
Kết luận: Vì u₁ ⋅ u₂ = 0, nên hai đường thẳng d₁ và d₂ vuông góc với nhau.

6. Mở Rộng: Đường Thẳng Vuông Góc Với Mặt Phẳng

Một đường thẳng được gọi là vuông góc với một mặt phẳng nếu nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó. Điều kiện để đường thẳng d có vectơ chỉ phương u vuông góc với mặt phẳng (P) có vectơ pháp tuyến n là: u và n cùng phương, tức là u = k.n với k là một số thực khác 0.

7. Lời Khuyên Khi Học Lý Thuyết Hai Đường Thẳng Vuông Góc

Nắm vững định nghĩa và điều kiện của hai đường thẳng vuông góc.
Luyện tập nhiều bài tập để hiểu rõ cách áp dụng lý thuyết vào giải quyết các bài toán cụ thể.
Kết hợp lý thuyết với hình vẽ để có cái nhìn trực quan và dễ hiểu hơn.
Tham khảo thêm các tài liệu học tập và bài giảng trực tuyến để mở rộng kiến thức.

Hy vọng bài viết này đã giúp các em hiểu rõ hơn về lý thuyết hai đường thẳng vuông góc trong chương trình Toán 11 Cánh Diều. Chúc các em học tập tốt và đạt kết quả cao!