Bài 3 trang 40 SGK Toán 11 tập 1 - Cánh diều
Tổng quan nội dung
Bài 3 trang 40 SGK Toán 11 Tập 1 - Cánh Diều: Giải bài tập về giới hạn lượng giác
Bài 3 thuộc chương trình Toán 11 Tập 1, tập trung vào việc rèn luyện kỹ năng tính giới hạn lượng giác. Bài tập này yêu cầu học sinh vận dụng các công thức và phương pháp đã học để giải quyết các bài toán cụ thể.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Dùng đồ thị hàm số y = sinx, y = cosx để xác định số nghiệm của phương trình:
Đề bài
Dùng đồ thị hàm số y = sinx, y = cosx để xác định số nghiệm của phương trình:
a) \(3\sin x + 2 = 0\) trên đoạn \(\left( { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right)\)
b) \(\cos x = 0\) trên đoạn \(\left[ { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\)
Phương pháp giải - Xem chi tiết
Dựa vào cách vẽ đồ thị đã học để xác định.
Lời giải chi tiết
a) Vẽ đồ thị:
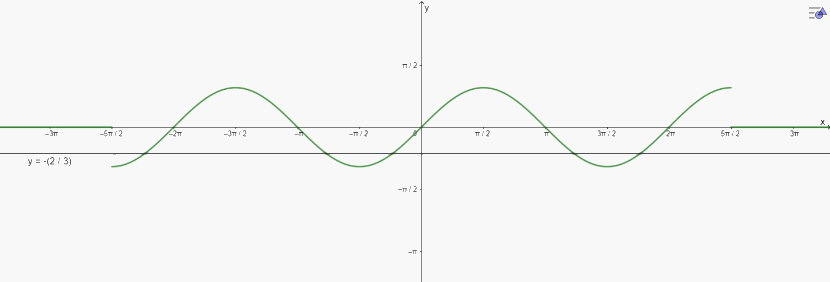
\(3\sin x + 2 = 0\) trên đoạn \(\left( { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right)\) có 5 nghiệm
b) Vẽ đồ thị:
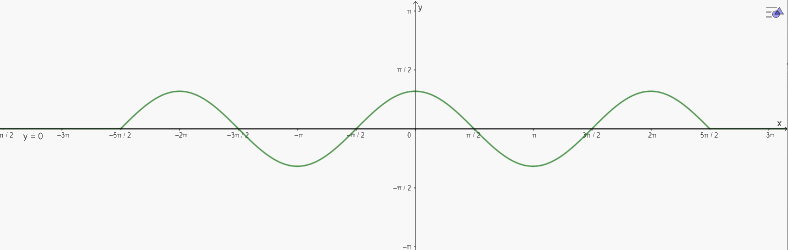
\(\cos x = 0\) trên đoạn \(\left[ { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\) có 6 nghiệm
Bài 3 trang 40 SGK Toán 11 Tập 1 - Cánh Diều: Giải chi tiết và hướng dẫn
Bài 3 trang 40 SGK Toán 11 Tập 1 - Cánh Diều là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về giới hạn lượng giác. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Nội dung bài tập
Bài 3 yêu cầu tính các giới hạn lượng giác sau:
- a) limx→0 (sin 2x / x)
- b) limx→0 (tan x / x)
- c) limx→π/4 (sin(x - π/4) / (x - π/4))
Lời giải chi tiết
a) limx→0 (sin 2x / x)
Ta có thể sử dụng công thức limx→0 (sin ax / x) = a. Đặt 2x = t, khi x → 0 thì t → 0. Vậy:
limx→0 (sin 2x / x) = limt→0 (sin t / (t/2)) = 2 * limt→0 (sin t / t) = 2 * 1 = 2
b) limx→0 (tan x / x)
Ta có thể viết tan x = sin x / cos x. Vậy:
limx→0 (tan x / x) = limx→0 (sin x / (x * cos x)) = limx→0 (sin x / x) * limx→0 (1 / cos x) = 1 * (1/1) = 1
c) limx→π/4 (sin(x - π/4) / (x - π/4))
Đặt t = x - π/4. Khi x → π/4 thì t → 0. Vậy:
limx→π/4 (sin(x - π/4) / (x - π/4)) = limt→0 (sin t / t) = 1
Hướng dẫn giải bài tập tương tự
Để giải các bài tập tương tự, bạn cần:
- Nhận biết các công thức giới hạn lượng giác cơ bản: limx→0 (sin x / x) = 1, limx→0 (tan x / x) = 1, limx→0 (1 - cos x) / x2 = 1/2
- Sử dụng các phép biến đổi đại số để đưa bài toán về dạng các công thức giới hạn đã biết.
- Lưu ý đến các điều kiện xác định của hàm số.
Ví dụ minh họa thêm
Tính limx→0 (sin 5x / x). Áp dụng công thức limx→0 (sin ax / x) = a, ta có:
limx→0 (sin 5x / x) = 5
Luyện tập thêm
Để nắm vững kiến thức, bạn nên luyện tập thêm các bài tập khác trong SGK và các tài liệu tham khảo. tusach.vn cung cấp nhiều bài tập luyện tập và lời giải chi tiết để bạn tham khảo.
Kết luận
Bài 3 trang 40 SGK Toán 11 Tập 1 - Cánh Diều là một bài tập quan trọng giúp học sinh hiểu rõ hơn về giới hạn lượng giác. Việc nắm vững các công thức và phương pháp giải bài tập sẽ giúp bạn tự tin hơn trong các kỳ thi.
| Công thức | Mô tả |
|---|---|
| limx→0 (sin x / x) = 1 | Giới hạn của sin x khi x tiến tới 0 |
| limx→0 (tan x / x) = 1 | Giới hạn của tan x khi x tiến tới 0 |