Lý thuyết Góc lượng giác. Giá trị lượng giác của góc lượng giác - SGK Toán 11 Cánh Diều
Tổng quan nội dung
Lý Thuyết Góc Lượng Giác - Nền Tảng Toán 11
Góc lượng giác là một khái niệm quan trọng trong chương trình Toán 11, đặc biệt là trong sách giáo khoa Cánh Diều. Hiểu rõ lý thuyết này sẽ giúp bạn giải quyết các bài toán liên quan đến lượng giác một cách dễ dàng và hiệu quả.
Bài viết này sẽ cung cấp đầy đủ kiến thức về góc lượng giác, giá trị lượng giác của góc lượng giác, cùng với các ví dụ minh họa và bài tập thực hành.
I. Góc lượng giác
I. Góc lượng giác
1. Góc hình học và số đo của chúng
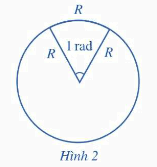
*Nhận xét:
- Đơn vị đo góc: độ hoặc radian (rad).
- Ta có: \({180^o} = \pi \)rad, do đó 1 rad \( = {\left( {\frac{{180}}{\pi }} \right)^o}\), \({1^o} = \left( {\frac{\pi }{{180}}} \right)\)rad.
- Người ta thường không viết chữ radian hay rad sau số đo góc.
VD: \(\frac{\pi }{2}\)rad cũng được viết là \(\frac{\pi }{2}\).
2. Góc lượng giác và số đo của chúng
a, Khái niệm
- Cho 2 tia Ou, Ov. Nếu tia Om quay chỉ theo chiều dương (hay chỉ theo chiều âm) xuất phát từ Ou đến trùng với tia Ov thì ta nói: Tia Om quét một góc lượng giác với tia đầu Ou và tia cuối Ov.
Kí hiệu: (Ou, Ov).
- Mỗi góc lượng giác được xác định bởi tia đầu Ou, tia cuối Ov và số đo của góc đó.
b, Tính chất
- Cho hai góc lượng giác = và (O’u’,O’v’) có tia đầu trùng nhau \(\left( {Ou \equiv O'u'} \right)\), tia cuối trùng nhau \(\left( {Ov \equiv O'v'} \right)\).
Khi đó, nếu sử dụng đợn vị đo là độ thì ta có:
\(\left( {Ou,Ov} \right) = \left( {O'u',O'v'} \right) + k{360^o},k \in \mathbb{Z}.\)
Nếu sử dụng đơn vị đo là radian thì:
\(\left( {Ou,Ov} \right) = \left( {O'u',O'v'} \right) + k2\pi ,k \in \mathbb{Z}.\)
* Hệ thức Chasles
Với 3 tia Ou, Ov, Ow bất kì ta có:
(Ou,Ov) + (Ov, Ow) = (Ou,Ow) \( + k2\pi ,k \in \mathbb{Z}.\)
II. Giá trị lượng giác của góc lượng giác
1. Đường tròn lượng giác
Trong mặt phẳng toa độ đã được định hướng Oxy, lấy điểm A(1;0). Đường tròn tâm O, bán kính OA = 1 được gọi là đường tròn lượng giác (hay đường tròn đơn vị) gốc A.
2. Giá trị lượng giác của góc lượng giác
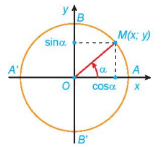
- Trục tung là trục sin, trục hoành là trục côsin.
- Điểm M(x;y) nằm trên đường tròn như hình vẽ. Khi đó:
\(x = \)cos\(\alpha \), \(y = \)sin\(\alpha \).
tan\(\alpha \)\( = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{y}{x}\left( {x \ne 0} \right)\)
\(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{x}{y}\left( {y \ne 0} \right)\)
* Dấu của các giá trị lượng giác của góc \(\alpha \)
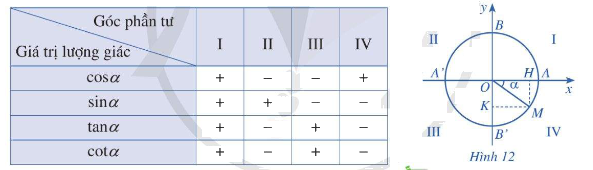
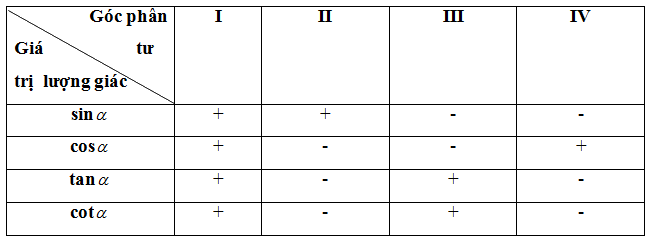
* Các công thức lượng giác cơ bản
\(\begin{array}{l}{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\left( {\alpha \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right)\\1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\left( {\alpha \ne k\pi ,k \in \mathbb{Z}} \right)\\\tan \alpha .\cot \alpha = 1\left( {\alpha \ne \frac{{k\pi }}{2},k \in \mathbb{Z}} \right)\end{array}\)
3. Giá trị lượng giác của các góc có liên quan đặc biệt
- Hai góc đối nhau \(\alpha \) và \( - \alpha \)
\(\begin{array}{l}\sin \left( { - \alpha } \right) = - \sin \alpha \\\cos \left( { - \alpha } \right) = \cos \alpha \\\tan \left( { - \alpha } \right) = - \tan \alpha \\\cot \left( { - \alpha } \right) = - \cot \alpha \end{array}\)
- Hai góc bù nhau (\(\alpha \) và \(\pi \)-\(\alpha \))
\(\begin{array}{l}\sin \left( {\pi - \alpha } \right) = \sin \alpha \\\cos \left( {\pi - \alpha } \right) = - \cos \alpha \\\tan \left( {\pi - \alpha } \right) = - \tan \alpha \\\cot \left( {\pi - \alpha } \right) = - \cot \alpha \end{array}\)
- Hai góc phụ nhau (\(\alpha \) và \(\frac{\pi }{2}\)-\(\alpha \))
\(\begin{array}{l}\sin \left( {\frac{\pi }{2} - \alpha } \right) = c{\rm{os}}\alpha \\\cos \left( {\frac{\pi }{2} - \alpha } \right) = \sin \alpha \\\tan \left( {\frac{\pi }{2} - \alpha } \right) = \cot \alpha \\\cot \left( {\frac{\pi }{2} - \alpha } \right) = \tan \alpha \end{array}\)
- Hai góc hơn kém \(\pi \)(\(\alpha \) và \(\pi \) + \(\alpha \))
\(\begin{array}{l}\sin \left( {\pi + \alpha } \right) = - \sin \alpha \\\cos \left( {\pi + \alpha } \right) = - \cos \alpha \\\tan \left( {\pi + \alpha } \right) = \tan \alpha \\\cot \left( {\pi + \alpha } \right) = \cot \alpha \end{array}\)
4. Sử dụng máy tính cầm tay để tính giá trị của một góc lượng giác
Đơn vị độ:

Đơn vị radian:

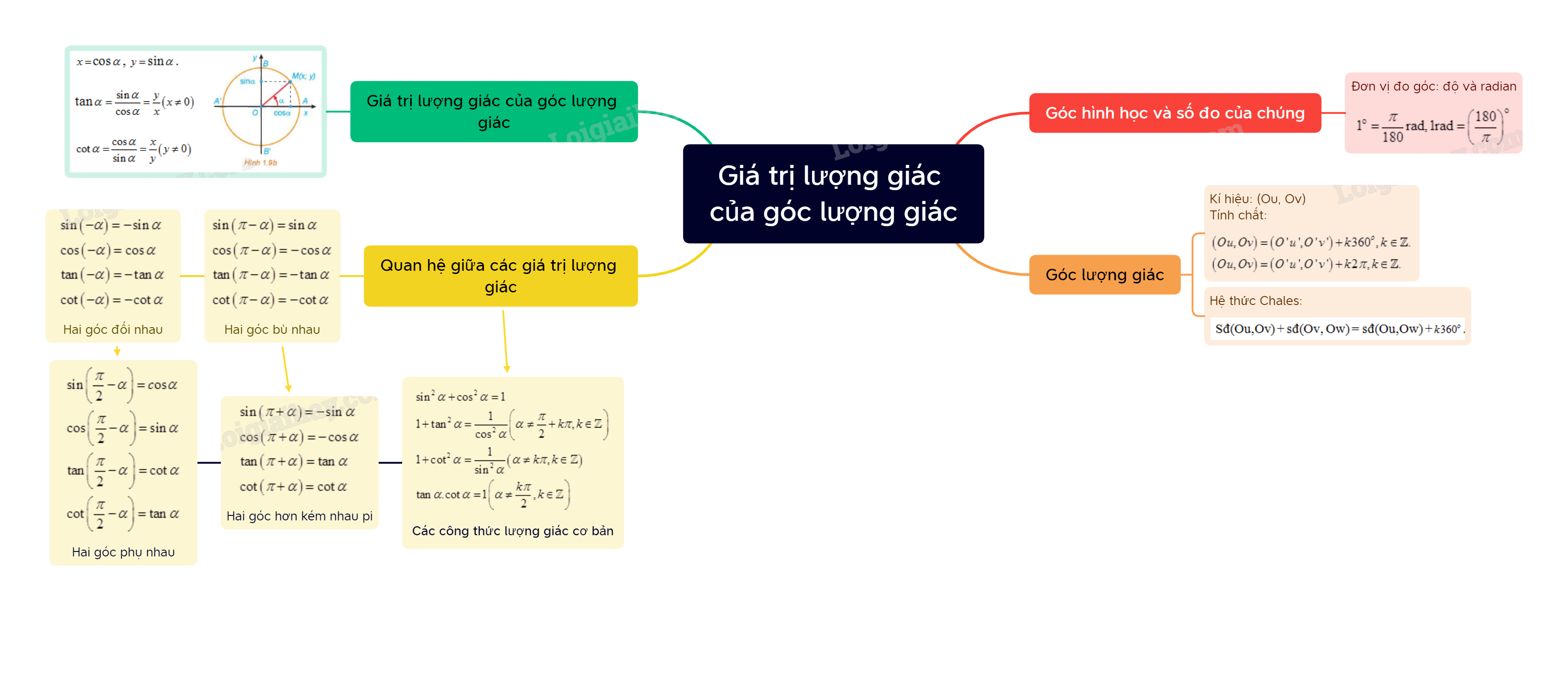
Lý Thuyết Góc Lượng Giác - Toán 11 Cánh Diều
Góc lượng giác là một khái niệm cơ bản và quan trọng trong toán học, đặc biệt là trong chương trình Toán 11. Nó mở rộng khái niệm góc hình học quen thuộc, cho phép chúng ta đo các góc lớn hơn 360 độ và làm nền tảng cho việc nghiên cứu các hàm lượng giác.
1. Khái Niệm Góc Lượng Giác
Trong mặt phẳng tọa độ Oxy, một góc lượng giác α được xác định bởi hai tia Om và On. Tia Om là tia gốc, tia On là tia cuối. Góc lượng giác được đo bằng độ (°) hoặc radian (rad). Chiều dương của việc quay là ngược chiều kim đồng hồ.
- Độ: Một vòng tròn đầy đủ là 360°.
- Radian: Một radian là góc ở tâm của một vòng tròn chắn một cung có độ dài bằng bán kính của vòng tròn đó. Mối quan hệ giữa độ và radian: 180° = π rad.
2. Đường Tròn Lượng Giác
Đường tròn lượng giác là đường tròn đơn vị (bán kính bằng 1) có tâm tại gốc tọa độ O. Mỗi điểm M trên đường tròn lượng giác tương ứng với một góc lượng giác α.
Tọa độ của điểm M(x, y) trên đường tròn lượng giác liên quan đến các giá trị lượng giác của góc α:
- x = cos α
- y = sin α
3. Giá Trị Lượng Giác của Góc Lượng Giác
Các giá trị lượng giác cơ bản của góc α bao gồm:
- Sin (sin α): Tỷ số giữa độ dài cạnh đối và độ dài cạnh huyền trong tam giác vuông.
- Cosin (cos α): Tỷ số giữa độ dài cạnh kề và độ dài cạnh huyền trong tam giác vuông.
- Tangent (tan α): Tỷ số giữa độ dài cạnh đối và độ dài cạnh kề trong tam giác vuông. tan α = sin α / cos α
- Cotangent (cot α): Tỷ số giữa độ dài cạnh kề và độ dài cạnh đối trong tam giác vuông. cot α = cos α / sin α
4. Bảng Giá Trị Lượng Giác của Các Góc Đặc Biệt
| Góc (α) | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| sin α | 0 | 1/2 | √2/2 | √3/2 | 1 |
| cos α | 1 | √3/2 | √2/2 | 1/2 | 0 |
| tan α | 0 | 1/√3 | 1 | √3 | Không xác định |
| cot α | Không xác định | √3 | 1 | 1/√3 | 0 |
5. Các Công Thức Lượng Giác Cơ Bản
Các công thức lượng giác giúp chúng ta biến đổi và đơn giản hóa các biểu thức lượng giác:
- sin2 α + cos2 α = 1
- tan α = sin α / cos α
- cot α = cos α / sin α
- 1 + tan2 α = 1/cos2 α
- 1 + cot2 α = 1/sin2 α
6. Bài Tập Vận Dụng
Để hiểu rõ hơn về lý thuyết góc lượng giác, bạn có thể thực hành các bài tập sau:
- Tính giá trị lượng giác của góc 120°.
- Chứng minh đẳng thức: sin2 α + cos2 α = 1.
- Giải phương trình lượng giác: sin α = 1/2.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về lý thuyết góc lượng giác trong chương trình Toán 11 Cánh Diều. Chúc bạn học tập tốt!