Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Lý thuyết Dãy số - SGK Toán 11 Cánh Diều
SGK Toán 11 - Cánh diều
Toán 11 tập 1 - Cánh Diều
Chương 2 Dãy số, cấp số cộng và cấp số nhân
Bài 1. Dãy số

Lý thuyết Dãy số - SGK Toán 11 Cánh Diều

Lý thuyết Dãy số - SGK Toán 11 Cánh Diều

Chào mừng bạn đến với chuyên mục Lý thuyết Dãy số của chương trình Toán 11 Cánh Diều tại tusach.vn!

Ở bài học này, chúng ta sẽ cùng nhau khám phá những khái niệm cơ bản về dãy số, các loại dãy số đặc biệt như cấp số cộng, cấp số nhân, và cách tính giới hạn của dãy số.

Tusach.vn cung cấp tài liệu học tập đầy đủ, dễ hiểu, giúp bạn tự tin chinh phục môn Toán 11.

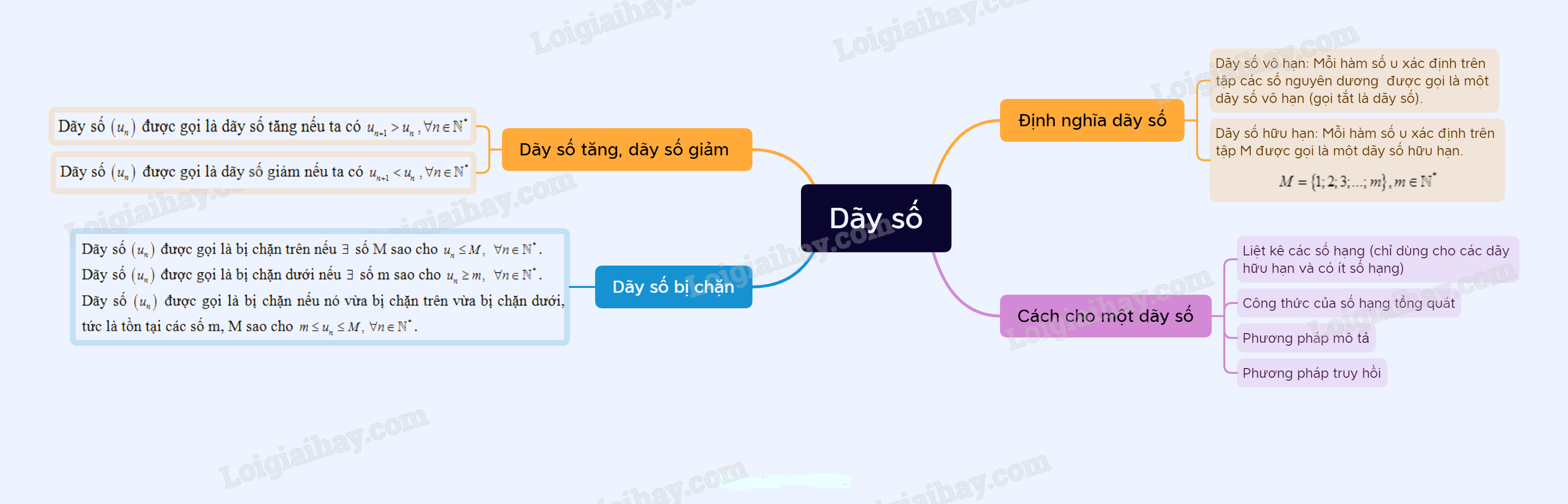
I. Khái niệm

I. Khái niệm

  • Dãy số hữu hạn

Mỗi hàm số u: \(\left\{ {1;2;3;...;m} \right\} \to \mathbb{R}\left( {m \in {\mathbb{N}^*}} \right)\) được gọi là một dãy số hữu hạn.

Do mỗi số nguyên dương \(k\left( {1 \le k \le m} \right)\) tương ứng với đúng một số \({u_k}\) nên ta có thể viết dãy số đó dưới dạng khai triển: \({u_1},{u_2},{u_3},...,{u_m}\)

Số \({u_1}\) là số hạng đầu; \({u_m}\) là số hạng cuối cùng của dãy số đó.

  • Dãy số vô hạn

Mỗi hàm số u: \({\mathbb{N}^*} \to \mathbb{R}\) được gọi là một dãy số vô hạn.

Do mỗi số nguyên dương \(n\) tương ứng với đúng một số \({u_n}\) nên ta có thể viết dãy số đó dưới dạng khai triển: \({u_1},{u_2},{u_3},...,{u_n},...\)

Số \({u_1}\) là số hạng đầu; \({u_n}\) là số hạng thứ n và gọi là số hạng tổng quát của dãy số.

2. Cách cho một dãy số

Một dãy số có thể cho bằng:

  • Liệt kê các số hạng (chỉ dùng cho các dãy hữu hạn và có ít số hạng).
  • Công thức của số hạng tổng quát.
  • Diễn đạt bằng lời cách xác định mỗi số hạn tổng quát của dãy số đó.
  • Phương pháp truy hồi.

3. Dãy số tăng, dãy số giảm

  • Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số tăng nếu ta có \({u_{n + 1}} > {u_n}\)\(,\forall n \in {\mathbb{N}^*}\).
  • Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số giảm nếu ta có \({u_{n + 1}} < {u_n}\)\(,\forall n \in {\mathbb{N}^*}\).

4. Dãy số bị chặn

  • Dãy số \(\left( {{u_n}} \right)\) được gọi là bị chặn trên nếu \(\exists \) số M sao cho \({u_n} \le M,\) \(\forall n \in {\mathbb{N}^*}\).
  • Dãy số \(\left( {{u_n}} \right)\) được gọi là bị chặn dưới nếu \(\exists \) số m sao cho \({u_n} \ge m,\) \(\forall n \in {\mathbb{N}^*}\).
  • Dãy số \(\left( {{u_n}} \right)\) được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, tức là tồn tại các số m, M sao cho \(m \le {u_n} \le M,\)\(\forall n \in {\mathbb{N}^*}\).

Lý thuyết Dãy số - SGK Toán 11 Cánh Diều 1

Lý Thuyết Dãy Số - SGK Toán 11 Cánh Diều: Tổng Quan và Hướng Dẫn Chi Tiết

Dãy số là một khái niệm nền tảng trong chương trình Toán học, đặc biệt quan trọng ở lớp 11. Việc nắm vững lý thuyết dãy số không chỉ giúp bạn giải quyết các bài tập trong SGK Toán 11 Cánh Diều mà còn là bước đệm quan trọng cho các kiến thức nâng cao hơn trong tương lai.

1. Khái Niệm Cơ Bản về Dãy Số

Một dãy số là một hàm số u được xác định trên tập hợp các số tự nhiên (hoặc một tập con của nó) và nhận giá trị là các số thực. Ký hiệu: (un), với un là số hạng thứ n của dãy số.

  • Số hạng tổng quát: Công thức xác định số hạng thứ n của dãy số.
  • Dãy số hữu hạn: Dãy số có số lượng số hạng là hữu hạn.
  • Dãy số vô hạn: Dãy số có số lượng số hạng là vô hạn.

2. Các Loại Dãy Số Đặc Biệt

Trong chương trình Toán 11 Cánh Diều, chúng ta sẽ tìm hiểu kỹ về hai loại dãy số đặc biệt:

  1. Cấp số cộng: Dãy số mà mỗi số hạng sau được tạo thành bằng cách cộng một số không đổi (công sai) vào số hạng đứng trước. Công thức: un+1 = un + d.
  2. Cấp số nhân: Dãy số mà mỗi số hạng sau được tạo thành bằng cách nhân số hạng đứng trước với một số không đổi (công bội) khác 0. Công thức: un+1 = un * q.

3. Giới Hạn của Dãy Số

Giới hạn của dãy số là giá trị mà các số hạng của dãy số tiến tới khi n tiến tới vô cùng. Việc tìm hiểu về giới hạn dãy số giúp chúng ta hiểu rõ hơn về hành vi của dãy số khi số lượng số hạng tăng lên.

Định nghĩa: Dãy số (un) có giới hạn là L nếu với mọi ε > 0, tồn tại số tự nhiên N sao cho với mọi n > N, ta có |un - L| < ε.

4. Bài Tập Vận Dụng và Ví Dụ Minh Họa

Để hiểu rõ hơn về lý thuyết dãy số, chúng ta hãy xem xét một số ví dụ minh họa:

Dãy sốLoại dãy sốGiới hạn
1, 2, 3, 4, ...Cấp số cộng∞
2, 4, 8, 16, ...Cấp số nhân∞
1/2, 1/4, 1/8, 1/16, ...Cấp số nhân0

5. Mẹo Học Tập và Luyện Tập Hiệu Quả

Để học tốt lý thuyết dãy số, bạn nên:

  • Nắm vững các định nghĩa và công thức cơ bản.
  • Luyện tập thường xuyên với các bài tập khác nhau.
  • Tìm hiểu các ứng dụng thực tế của dãy số.
  • Sử dụng các tài liệu tham khảo và nguồn học tập trực tuyến.

Tusach.vn hy vọng rằng với những kiến thức và hướng dẫn chi tiết trên, bạn sẽ tự tin chinh phục phần Lý thuyết Dãy số trong SGK Toán 11 Cánh Diều. Chúc bạn học tập tốt!

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN