Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải mục 2 trang 30, 31 SGK Toán 11 tập 2 - Cánh Diều
SGK Toán 11 - Cánh diều
Giải Toán 11 tập 2 - Cánh Diều
Chương VI. Hàm số mũ và hàm số lôgarit
Bài 1. Phép tính lũy thừa với số mũ thực

Giải mục 2 trang 30, 31 SGK Toán 11 tập 2 - Cánh Diều

Giải mục 2 trang 30, 31 SGK Toán 11 tập 2 - Cánh Diều

Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Toán 11 tập 2 - Cánh Diều. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.

Bài viết này sẽ giúp bạn giải quyết triệt để các bài tập trong mục 2 trang 30, 31, đảm bảo bạn hiểu rõ bản chất và phương pháp giải.

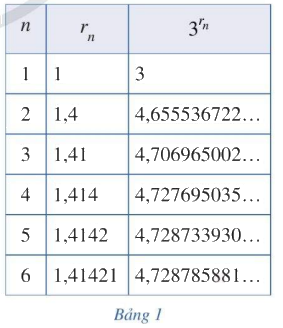
Xét số vô tỉ: (sqrt 2 = 1,4142135624...). Xét dãy số hữu tỉ: ({r_1} = 1;{r_2} = 1,4;{r_3} = 1,41;{r_4} = 1,414;{r_5} = 1,4142;{r_6} = 1,41421;...)

HĐ 5LT 5HĐ 6LT 6LT 7

HĐ 5

    Xét số vô tỉ: \(\sqrt 2 = 1,4142135624...\). Xét dãy số hữu tỉ: \({r_1} = 1;{r_2} = 1,4;{r_3} = 1,41;{r_4} = 1,414;{r_5} = 1,4142;{r_6} = 1,41421;...\) và \(\lim {r_n} = \sqrt 2 \). Bằng cách tính \({3^{{r_n}}}\) tương ứng, ta nhận được Bảng 1 ghi các dãy số \(\left( {{r_n}} \right)\) và \(\left( {{3^{{r_n}}}} \right)\) với n = 1, 2, …, 6. Người ta chứng minh được rằng khi \(n \to + \infty \) thì dãy số \(\left( {{3^{{r_n}}}} \right)\) dần đến một giới hạn mà ta gọi là \({3^{\sqrt 2 }}\). Nêu dự đoán về giá trị của số \({3^{\sqrt 2 }}\) (đến hàng phần trăm).

    Giải mục 2 trang 30, 31 SGK Toán 11 tập 2 - Cánh Diều 1

    Phương pháp giải:

    Dựa vào giới hạn của dãy số hữu tỉ để dự đoán

    Lời giải chi tiết:

    Do \({r_1} = 1;{r_2} = 1,4;{r_3} = 1,41;{r_4} = 1,414;{r_5} = 1,4142;{r_6} = 1,41421;...\) => \({3^{\sqrt 2 }} \approx 1,41\)

    LT 5

      So sánh \({10^{\sqrt 2 }}\,\,và \,\,10\)

      Phương pháp giải:

      Dựa vào dự đoán ở ví dụ 5 để so sánh

      Lời giải chi tiết:

      Do \({10^{\sqrt 2 }} \approx 25,95 > 10 \Rightarrow {10^{\sqrt 2 }} > 10\)

      HĐ 6

        Nêu những tính chất của phép tính lũy thừa với số mũ nguyên của một số thực dương

        Phương pháp giải:

        Dựa vào các kiến thức đã học về lũy thừa ở cấp 2 để làm bài

        Lời giải chi tiết:

        + \({a^\alpha }.{a^\beta } = {a^{\alpha + \beta }}\)

        + \(\frac{{{a^\alpha }}}{{{a^\beta }}} = {a^{\alpha - \beta }}\)

        + \({\left( {{a^\alpha }} \right)^\beta } = {a^{\alpha .\beta }}\)

        + \({(ab)^\alpha } = {a^\alpha }.{b^\alpha }\)

        + \({\left( {\frac{a}{b}} \right)^\alpha } = \frac{{{a^\alpha }}}{{{b^\alpha }}}\)

        + Nếu a > 1 thì \({a^\alpha } > {a^\beta } \Leftrightarrow \alpha < \beta \)

        + Nếu 0 < a < 1 thì \({a^\alpha } > {a^\beta } \Leftrightarrow \alpha > \beta \)

        LT 6

          Không sử dụng máy tính cầm tay, hãy so sánh các số: \({2^{2\sqrt 3 }}\,\,và \,\,{2^{3\sqrt 2 }}\)

          Phương pháp giải:

          Dựa vào Ví dụ 7 để làm

          Lời giải chi tiết:

          Ta có:

          \(\left. \begin{array}{l}{\left( {2\sqrt 3 } \right)^2} = 12\\{\left( {3\sqrt 2 } \right)^2} = 18\end{array} \right\} \Rightarrow 2\sqrt 3 < 3\sqrt 2 \Rightarrow {2^{2\sqrt 3 }} < {2^{3\sqrt 2 }}\)

          LT 7

            Dùng máy tính cầm tay để tính (làm tròn kết quả đến hàng phần trăm):

            a) \( (-2,7)^{-4}\);

            b) \( \sqrt 3 - 1)^{\sqrt[3] {4} + 1}\)

            Phương pháp giải:

            Sử dụng máy tính để tính, làm tròn đến hàng phần trăm.

            Lời giải chi tiết:

            a) \( (-2,7)^{-4} \approx 0,02\);

            b) \( \sqrt 3 - 1)^{\sqrt[3] {4} + 1} \approx 0,45\)

            Giải mục 2 trang 30, 31 SGK Toán 11 tập 2 - Cánh Diều: Hướng dẫn chi tiết và dễ hiểu

            Mục 2 của chương trình Toán 11 tập 2 - Cánh Diều thường tập trung vào các kiến thức về phép biến hình, bao gồm phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc nắm vững các phép biến hình này là nền tảng quan trọng để học tập các kiến thức hình học nâng cao hơn.

            Nội dung chính của Mục 2 trang 30, 31

            • Phép tịnh tiến: Định nghĩa, tính chất, và ứng dụng của phép tịnh tiến trong hình học.
            • Phép quay: Định nghĩa, tính chất, và cách xác định tâm quay, góc quay.
            • Phép đối xứng trục: Định nghĩa, tính chất, và cách xác định trục đối xứng.
            • Phép đối xứng tâm: Định nghĩa, tính chất, và cách xác định tâm đối xứng.
            • Bài tập vận dụng: Các bài tập giúp học sinh rèn luyện kỹ năng áp dụng các phép biến hình vào giải quyết các bài toán hình học cụ thể.

            Giải chi tiết các bài tập trong Mục 2 trang 30, 31

            Dưới đây là giải chi tiết các bài tập trong Mục 2 trang 30, 31 SGK Toán 11 tập 2 - Cánh Diều:

            Bài 1: (Trang 30)

            Đề bài: Cho điểm A(1; 2) và vector v = (3; -1). Tìm tọa độ điểm A' là ảnh của A qua phép tịnh tiến theo vector v.

            Giải:

            Tọa độ điểm A' được tính theo công thức: A'(xA + xv; yA + yv) = (1 + 3; 2 + (-1)) = (4; 1).

            Bài 2: (Trang 31)

            Đề bài: Cho tam giác ABC với A(0; 0), B(1; 0), C(0; 1). Tìm tọa độ các đỉnh của tam giác A'B'C' là ảnh của tam giác ABC qua phép quay tâm O(0; 0) góc 90o.

            Giải:

            Sử dụng công thức quay điểm quanh gốc tọa độ:

            • A'(xAcosθ - yAsinθ; xAsinθ + yAcosθ) = (0; 0)
            • B'(xBcosθ - yBsinθ; xBsinθ + yBcosθ) = (0; 1)
            • C'(xCcosθ - yCsinθ; xCsinθ + yCcosθ) = (-1; 0)

            Mẹo giải nhanh các bài tập về phép biến hình

            • Nắm vững định nghĩa và tính chất: Hiểu rõ định nghĩa và tính chất của từng phép biến hình là bước đầu tiên để giải quyết các bài toán.
            • Sử dụng công thức: Ghi nhớ và áp dụng chính xác các công thức liên quan đến phép biến hình.
            • Vẽ hình minh họa: Vẽ hình minh họa giúp bạn hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.
            • Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.

            Tại sao nên chọn tusach.vn để học Toán 11?

            tusach.vn cung cấp:

            • Lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 11 tập 2 - Cánh Diều.
            • Đội ngũ giáo viên giàu kinh nghiệm, nhiệt tình hỗ trợ học sinh.
            • Giao diện thân thiện, dễ sử dụng.
            • Cập nhật kiến thức mới nhất, đáp ứng yêu cầu của chương trình học.

            Hãy truy cập tusach.vn ngay hôm nay để học Toán 11 hiệu quả và đạt kết quả cao!

            Phép biến hìnhCông thức
            Tịnh tiếnA'(xA + xv; yA + yv)
            QuayA'(xAcosθ - yAsinθ; xAsinθ + yAcosθ)

            Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

            CHỦ ĐỀ SÁCH XEM NHIỀU

            Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

            VỀ TUSACH.VN