Bài 6 trang 94 SGK Toán 11 tập 2 - Cánh diều
Tổng quan nội dung
Bài 6 trang 94 SGK Toán 11 tập 2 - Cánh Diều: Giải tích
Bài 6 trang 94 SGK Toán 11 tập 2 thuộc chương trình Giải tích, tập trung vào việc ứng dụng đạo hàm để khảo sát hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm, điểm cực trị, và khoảng đơn điệu của hàm số để giải quyết các bài toán cụ thể.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải bài tập Toán 11 hiệu quả.
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\). Gọi \(\alpha \) là số đo của góc nhị diện \(\left[ {A,BC,S} \right]\).
Đề bài
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\). Gọi \(\alpha \) là số đo của góc nhị diện \(\left[ {A,BC,S} \right]\). Chứng minh rằng tỉ số diện tích của hai tam giác \(ABC\) và \(SBC\) bằng \(\cos \alpha \).
Phương pháp giải - Xem chi tiết
‒ Cách xác định góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\)
Bước 1: Xác định \(c = \left( {{P_1}} \right) \cap \left( {{Q_1}} \right)\).
Bước 2: Tìm mặt phẳng \(\left( R \right) \supset c\).
Bước 3: Tìm \(p = \left( R \right) \cap \left( {{P_1}} \right),q = \left( R \right) \cap \left( {{Q_1}} \right),O = p \cap q,M \in p,N \in q\).
Khi đó \(\left[ {{P_1},d,{Q_1}} \right] = \widehat {MON}\).
Lời giải chi tiết
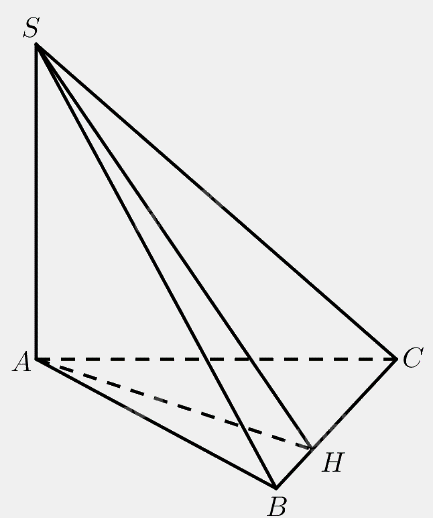
Kẻ \(AH \bot BC\left( {H \in BC} \right)\)
\(SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC\)
\( \Rightarrow BC \bot \left( {SAH} \right) \Rightarrow BC \bot SH\)
Vậy \(\widehat {SHA}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {A,BC,S} \right]\)
\( \Rightarrow \widehat {SHA} = \alpha \)
\(\begin{array}{l}{S_{\Delta ABC}} = \frac{1}{2}BC.AH,{S_{\Delta SBC}} = \frac{1}{2}BC.SH\\ \Rightarrow \frac{{{S_{\Delta ABC}}}}{{{S_{\Delta SBC}}}} = \frac{{\frac{1}{2}BC.AH}}{{\frac{1}{2}BC.SH}} = \frac{{AH}}{{SH}} = \cos \widehat {SHA} = \cos \alpha \end{array}\)
Bài 6 trang 94 SGK Toán 11 tập 2 - Cánh Diều: Giải chi tiết và hướng dẫn
Bài 6 trang 94 SGK Toán 11 tập 2 - Cánh Diều là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó trong việc khảo sát hàm số. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Nội dung bài tập
Bài tập yêu cầu khảo sát hàm số y = f(x) bằng cách xác định:
- Tập xác định của hàm số
- Các điểm cực trị của hàm số
- Khoảng đơn điệu của hàm số
- Giới hạn của hàm số tại vô cùng
- Vẽ đồ thị hàm số
Hướng dẫn giải
- Xác định tập xác định: Tìm các giá trị của x sao cho hàm số f(x) có nghĩa.
- Tính đạo hàm: Tính đạo hàm f'(x) của hàm số f(x).
- Tìm điểm cực trị: Giải phương trình f'(x) = 0 để tìm các điểm nghiệm. Sau đó, xét dấu của f'(x) để xác định các điểm cực đại, cực tiểu.
- Xác định khoảng đơn điệu: Dựa vào dấu của f'(x) để xác định khoảng đồng biến và khoảng nghịch biến của hàm số.
- Tính giới hạn: Tính các giới hạn của hàm số khi x tiến tới vô cùng, các điểm gián đoạn hoặc điểm cực trị.
- Vẽ đồ thị: Sử dụng các thông tin đã tìm được để vẽ đồ thị hàm số.
Ví dụ minh họa (Giả sử hàm số cụ thể là y = x^3 - 3x^2 + 2)
1. Tập xác định: Hàm số y = x^3 - 3x^2 + 2 có tập xác định là R (tập hợp tất cả các số thực).
2. Đạo hàm: y' = 3x^2 - 6x
3. Điểm cực trị: Giải phương trình y' = 0:
3x^2 - 6x = 0
3x(x - 2) = 0
=> x = 0 hoặc x = 2
Xét dấu y':
- x < 0: y' > 0 (hàm số đồng biến)
- 0 < x < 2: y' < 0 (hàm số nghịch biến)
- x > 2: y' > 0 (hàm số đồng biến)
Vậy hàm số có cực đại tại x = 0, y(0) = 2 và cực tiểu tại x = 2, y(2) = -2.
4. Khoảng đơn điệu:
- Hàm số đồng biến trên khoảng (-∞; 0) và (2; +∞)
- Hàm số nghịch biến trên khoảng (0; 2)
5. Giới hạn:
- lim (x→+∞) y = +∞
- lim (x→-∞) y = -∞
6. Vẽ đồ thị: Dựa vào các thông tin trên, ta có thể vẽ được đồ thị hàm số y = x^3 - 3x^2 + 2.
Lưu ý khi giải bài tập
- Đảm bảo hiểu rõ các khái niệm về đạo hàm, điểm cực trị, và khoảng đơn điệu.
- Thực hiện các bước giải một cách cẩn thận và chính xác.
- Kiểm tra lại kết quả để đảm bảo tính đúng đắn.
tusach.vn hy vọng với lời giải chi tiết và hướng dẫn trên, các bạn học sinh có thể tự tin giải Bài 6 trang 94 SGK Toán 11 tập 2 - Cánh Diều và đạt kết quả tốt trong môn học. Chúc các bạn học tập tốt!
| Khái niệm | Giải thích |
|---|---|
| Đạo hàm | Tốc độ thay đổi của hàm số tại một điểm. |
| Điểm cực trị | Điểm mà tại đó hàm số đạt giá trị lớn nhất hoặc nhỏ nhất trong một khoảng nào đó. |
| Khoảng đơn điệu | Khoảng mà trên đó hàm số luôn tăng hoặc luôn giảm. |