Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Bài 7 trang 120 SGK Toán 11 tập 1 - Cánh Diều
SGK Toán 11 - Cánh diều
Toán 11 tập 1 - Cánh Diều
Chương 4 Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
Bài tập cuối chương 4

Bài 7 trang 120 SGK Toán 11 tập 1 - Cánh Diều

Bài 7 trang 120 SGK Toán 11 tập 1 - Cánh Diều

Bài 7 thuộc chương trình học Toán 11 tập 1, sách Cánh Diều, tập trung vào việc rèn luyện kỹ năng giải bài toán liên quan đến phép biến hóa lượng giác. Bài tập này đòi hỏi học sinh nắm vững các công thức lượng giác cơ bản và khả năng vận dụng linh hoạt vào giải quyết vấn đề.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.

Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD) và AB = 2CD. Gọi M, N lần lượt là trung điểm của các cạnh SA, SB. Chứng minh rằng:

Đề bài

Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD) và AB = 2CD. Gọi M, N lần lượt là trung điểm của các cạnh SA, SB. Chứng minh rằng:

a) MN // (SCD);

b) DM // (SBC);

c) Lấy điểm I thuộc cạnh SD sao cho\(\frac{{SI}}{{SD}} = \frac{2}{3}\).Chứng minh rằng: SB // (AIC).

Phương pháp giải - Xem chi tiếtBài 7 trang 120 SGK Toán 11 tập 1 - Cánh Diều 1

Đường thẳng d song song với mặt phẳng (P) nếu d song song với 1 đường thẳng d' nằm trong (P).

Lời giải chi tiết

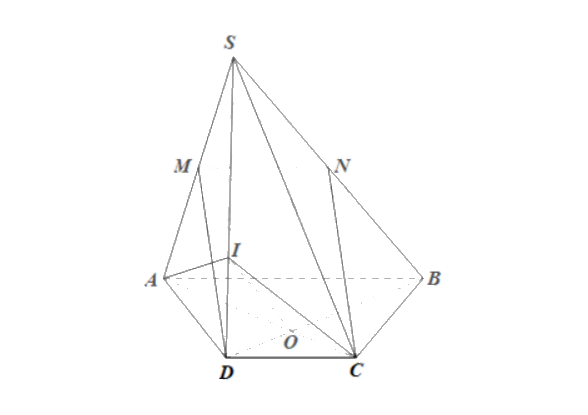
Bài 7 trang 120 SGK Toán 11 tập 1 - Cánh Diều 2

a) Trong mp(SAB), xét DSAB có M, N lần lượt là trung điểm của SA, SB nên MN là đường trung bình của tam giác

Do đó MN // AB.

Mà AB // CD (giả thiết) nên MN // CD.

Lại có CD ⊂ (SCD) nên MN // (SCD).

b) Theo câu a, MN là đường trung bình của ΔSAB nên MN = ½AB

Mà AB = 2CD hay CD = ½ AB

Do đó MN = CD.

Xét tứ giác MNCD có: MN // CD và MN = CD nên MNCD là hình bình hành

Suy ra DM // CN

Mà CN ⊂ (SBC) nên DM // (SBC)

c) Trong mp(ABCD), gọi O là giao điểm của AC và BD.

Do AB // CD, theo hệ quả định lí Thalès ta có: \(\frac{{OB}}{{DO}} = \frac{{AB}}{{CD}} = \frac{2}{1}\)

Suy ra\(\frac{{OB}}{{DO + OB}} = \frac{2}{{1 + 2}} = \frac{2}{3}\) hay \(OB\frac{{OB}}{{DO}} = \frac{2}{3}\)

• Trong mp(SDB), xét Δ∆SDB có \(\frac{{SI}}{{SD}} = \frac{{OB}}{{DB}} = \frac{2}{3}\) nên IO // SB (theo định lí Thalès đảo)

Mà IO ⊂ (AIC) nên SB // (AIC).

Bài 7 trang 120 SGK Toán 11 tập 1 - Cánh Diều: Giải chi tiết và hướng dẫn

Bài 7 trang 120 SGK Toán 11 tập 1 - Cánh Diều là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh củng cố kiến thức về phép biến hóa lượng giác. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:

Nội dung bài tập

Bài 7 yêu cầu học sinh giải các phương trình lượng giác, thường liên quan đến các công thức biến đổi lượng giác như công thức cộng, trừ, nhân đôi, chia đôi góc. Để giải bài tập này hiệu quả, học sinh cần nắm vững các công thức này và biết cách vận dụng chúng một cách linh hoạt.

Lời giải chi tiết

Để giải bài 7, chúng ta sẽ tiến hành các bước sau:

  1. Bước 1: Biến đổi phương trình lượng giác về dạng cơ bản. Sử dụng các công thức lượng giác để đưa phương trình về dạng sin(x) = a, cos(x) = a, tan(x) = a, hoặc cot(x) = a.
  2. Bước 2: Giải phương trình lượng giác cơ bản. Tìm các nghiệm của phương trình lượng giác cơ bản trong khoảng [0, 2π).
  3. Bước 3: Tìm tất cả các nghiệm của phương trình lượng giác. Thêm k2π vào mỗi nghiệm tìm được ở bước 2, với k là số nguyên.

Ví dụ: Giả sử phương trình cần giải là sin(x) = 1/2. Ta có:

  • Bước 1: Phương trình đã ở dạng cơ bản.
  • Bước 2: Nghiệm của phương trình sin(x) = 1/2 trong khoảng [0, 2π) là x = π/6 và x = 5π/6.
  • Bước 3: Tất cả các nghiệm của phương trình là x = π/6 + k2π và x = 5π/6 + k2π, với k là số nguyên.

Mẹo giải nhanh

Để giải nhanh các bài tập về phép biến hóa lượng giác, bạn có thể sử dụng một số mẹo sau:

  • Nắm vững các công thức lượng giác: Điều này là cơ bản để giải quyết mọi bài tập về lượng giác.
  • Sử dụng máy tính bỏ túi: Máy tính bỏ túi có thể giúp bạn tính toán nhanh chóng các giá trị lượng giác.
  • Luyện tập thường xuyên: Càng luyện tập nhiều, bạn càng trở nên thành thạo trong việc giải các bài tập về lượng giác.

Bài tập tương tự

Để củng cố kiến thức, bạn có thể làm thêm các bài tập tương tự sau:

  • Giải phương trình cos(x) = √3/2.
  • Giải phương trình tan(x) = 1.
  • Giải phương trình cot(x) = 0.

Kết luận

Bài 7 trang 120 SGK Toán 11 tập 1 - Cánh Diều là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải phương trình lượng giác. Bằng cách nắm vững các công thức lượng giác và luyện tập thường xuyên, bạn có thể tự tin giải quyết mọi bài tập về lượng giác.

Chúc bạn học tốt!

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN